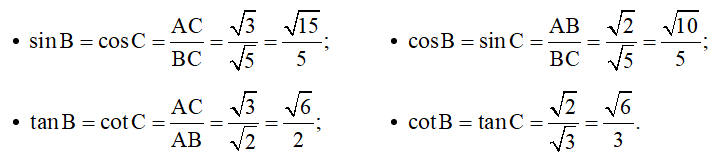Sách bài tập Toán 9 Bài 1 (Cánh diều): Tỉ số lượng giác của góc nhọn

Giải SBT Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn - Cánh diều

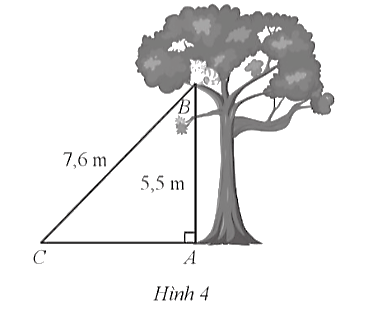
Bài 1 trang 81 SBT Toán 9 Tập 1: Hình 4 mô tả một con mèo bị mắc kẹt ở vị trí B trên cành cây với độ cao AB = 5,5 m. Để đưa con mèo xuống, người ta cần phải đặt thang dựa vào cành cây đó. Khoảng cách từ chân thang đến điểm chạm vào cành cây là BC = 7,6 m. Góc giữa thang với phương nằm ngang là góc BCA. Tính các tỉ số lượng giác của góc BCA (làm tròn kết quả đến hàng phần trăm).

Lời giải:

Trong tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

AB² + AC² = BC².

Suy ra AC² = BC² – AB² = 7,6² – 5,5² = 57,76 – 30,25 = 27,51.

Do đó $AC=\sqrt{27,51}( \text{m}).$

Tam giác ABC vuông tại A nên:

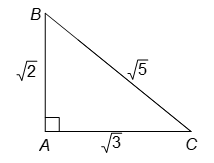
Bài 2 trang 81 SBT Toán 9 Tập 1: Cho tam giác ABC có $AB=\sqrt{2} \text{cm},$ $BC=\sqrt{5} \text{cm},$ $AC=\sqrt{3} \text{cm}.$ Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.

Lời giải:

Vì ${\left(\sqrt{2}\right)}^2+{\left(\sqrt{3}\right)}^2=2+3=5={\left(\sqrt{5}\right)}^2$ nên AB² + AC² = BC².

Do đó, theo định lí Pythagore đảo, ta có tam giác ABC vuông tại A.

Tam giác ABC vuông tại A nên $\widehat{B}$ và $\widehat{C}$ là hai góc phụ nhau, do đó:

Bài 3 trang 81 SBT Toán 9 Tập 1: Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giá trị mỗi biểu thức sau:

a) $\frac{\sin 39°}{\cos 51°};$

b) cos 37°30’ ‒ sin 52°30’;

c) tan 73° ‒ cot 17°;

d) cot 44°.cot 46°.

Lời giải:

a) Ta có: 39° + 51° = 90° nên 39° và 51° là hai góc phụ nhau, do đó:

$\frac{\sin 39°}{\cos 51°}=\frac{\cos 51°}{\cos 51°}=1.$

b) Ta có: 37°30’ + 52°30’ = 90° nên 37°30’ và 52°30’ là hai góc phụ nhau, do đó:

cos 37°30’ ‒ sin 52°30’ = sin 52°30’ ‒ sin 52°30’ = 0.

c) Ta có: 73° + 17° = 90° nên 73° và 17° là hai góc phụ nhau, do đó:

tan 73° ‒ cot 17° = cot 17° ‒ cot 17° = 0.

d) Ta có: 44° + 46° = 90° nên 44° và 46° là hai góc phụ nhau, do đó:

cot 44°.cot 46° = tan 46°.cot 46° = 1.

Bài 4 trang 82 SBT Toán 9 Tập 1: Sử dụng bảng tỉ số lượng giác của các góc nhọn đặc biệt, tính giá trị của mỗi biểu thức sau:

a) 2sin30° ‒ 2cos60° + tan45°;

b) sin45° + cot60°.cos30°.

Lời giải:

a) 2sin30° ‒ 2cos60° + tan45°

$=2\cdot \frac{1}{2}-2\cdot \frac{1}{2}+1=1-1+1=1.$

b) sin 45° + cot 60°.cos 30°

$=\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{3}\cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{2}}{2}+\frac{1}{2}=\frac{\sqrt{2}+1}{2}.$

Bài 5 trang 82 SBT Toán 9 Tập 1: Tính giá trị của mỗi biểu thức sau:

a) A = sin²79° + cos²79°;

b) B = tan73°.tan37°.tan53°.tan17°;

c) C = cos²73° + cos²53° + cos²17° + cos²37°;

d) D = sin59° + cos59° ‒ sin31° ‒ cos31°.

Lời giải:

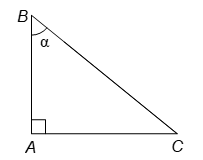
Xét tam giác ABC vuông tại A với $\widehat{B}=\alpha ,$ ta có:

$\sin \alpha =\frac{AC}{BC};$$\cos \alpha =\frac{AB}{BC}$ và AB² + AC² = BC² (định lí Pythagore).

Do đó ${\sin }^2\alpha +{\cos }^2\alpha ={\left(\frac{AB}{BC}\right)}^2+{\left(\frac{AC}{BC}\right)}^2$

$=\frac{A{B}^2}{B{C}^2}+\frac{A{C}^2}{B{C}^2}=\frac{A{B}^2+A{C}^2}{B{C}^2}=\frac{B{C}^2}{B{C}^2}=1.$

a) A = sin²79° + cos²79° = 1.

b) Do 73° + 17° = 90° và 37° + 53° = 90° nên:

B = tan 73°.tan 37°.tan 53°.tan 17°

= (tan 73° . tan 17°) (tan 37° . tan 53°)

= (tan 73° . cot 73°) (tan 37° . cot 37°)

= 1.1 = 1.

c) C = cos² 73° + cos² 53° + cos² 17° + cos² 37°

= (cos² 73° + cos² 17°) + (cos² 37° + cos² 53°)

= (sin² 17° + cos² 17°) + (sin² 53° + cos² 53°)

= 1 + 1 = 2.

d) Do 59° + 31° = 90° nên:

D = sin 59° + cos 59° ‒ sin 31° ‒ cos 31°.

= (sin 59° ‒ cos 31°) + (cos 59° ‒ sin 31°)

= (sin 59° ‒ sin 59°) + (sin 31° ‒ sin 31°)

= 0 + 0 = 0.

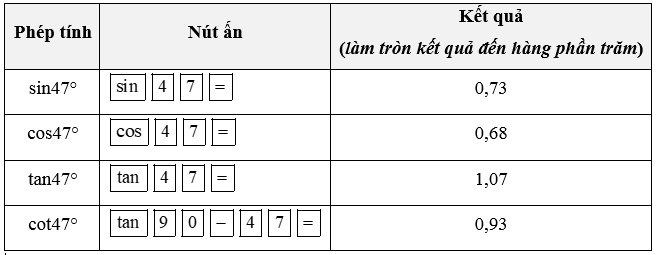
Bài 6 trang 82 SBT Toán 9 Tập 1: Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):

a) 47°;

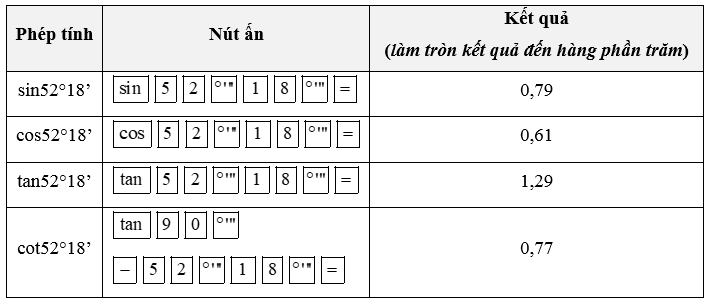
b) 52°18’;

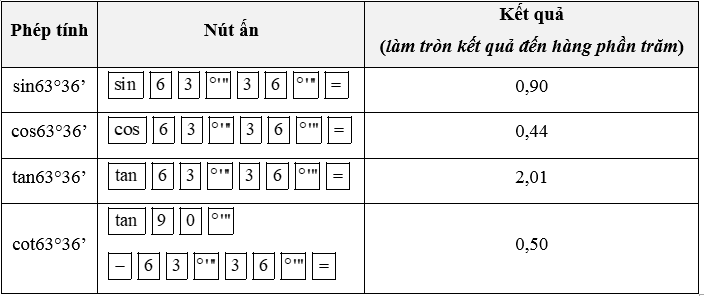
c) 63°36’;

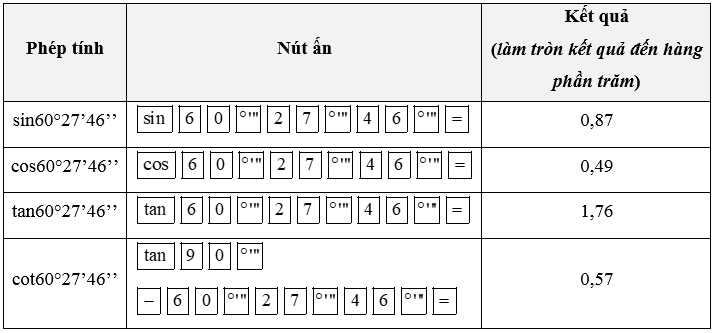
d) 60°27’46’’.

Lời giải:

Chú ý: Để tính cotα, ta sử dụng công thức cotα = tan(90° – α) hoặc $\cot \alpha =\frac{1}{\tan \alpha }.$

a) Ta có:

b) Ta có:

c) Ta có:

d) Ta có:

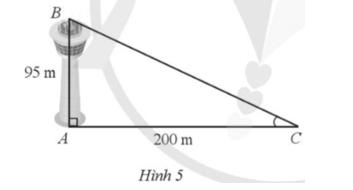
Bài 7 trang 82 SBT Toán 9 Tập 1: Một đài quan sát không lưu có độ cao là AB = 95 m. Ở một thời điểm nào đó vào ban ngày, Mặt Trời chiếu tạo bóng dài AC = 200 m trên mặt đất. Góc tạo bởi tia sáng Mặt Trời và phương nằm ngang là góc BCA (Hình 5). Tính số đo góc BCA (làm tròn kết quả đến hàng đơn vị của độ).

Lời giải:

Vì tam giác ABC vuông tại A nên $\tan \widehat{BCA}=\frac{AB}{AC}=\frac{95}{200}=0,475.$

Suy ra $\widehat{BCA}\approx 25°.$

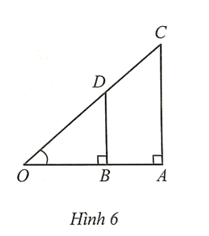
Bài 8 trang 82 SBT Toán 9 Tập 1: Cho Hình 6 có AB = 3 cm, CD = 4 cm. Tính số đo góc AOC (làm tròn kết quả đến hàng đơn vị của độ).

Lời giải:

Tam giác OAC có BD // AC (cùng vuông góc với OA) nên $\frac{OB}{OA}=\frac{OD}{OC}$ hay $\frac{OA}{OC}=\frac{OB}{OD}.$

Theo tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{OA}{OC}=\frac{OB}{OD}=\frac{OA-OB}{OC-OD}=\frac{AB}{CD}=\frac{3}{4}.$

Vì tam giác OAC vuông tại A nên $\cos \widehat{AOC}=\frac{OA}{OC}=\frac{3}{4}.$

Suy ra $\widehat{AOC}\approx 41°.$

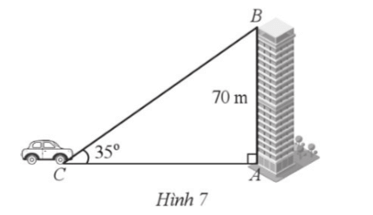
Bài 9 trang 82 SBT Toán 9 Tập 1: Từ vị trí B của toà nhà cao 70 m, một tia sáng chiếu xuống một ô tô đang đỗ tại vị trí C. Góc tạo bởi tia sáng và phương nằm ngang là $\widehat{ACB}=35°$ (Hình 7). Hỏi ô tô đỗ cách chân toà nhà (ở vị trí A) bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

Lời giải:

Vì tam giác ABC vuông tại A nên $\tan \widehat{BCA}=\frac{AB}{AC}.$

Suy ra $AC=\frac{AB}{\tan \widehat{ACB}}=\frac{70}{\tan 35°}\approx 99,97\left(m\right).$

Vậy ô tô đỗ cách chân toà nhà khoảng 99,97 m.

Xem thêm Lời giải bài tập Toán 9 sách Cánh diều hay, chi tiết khác:

Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài tập cuối chương 3

Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 3: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài tập cuối chương 4