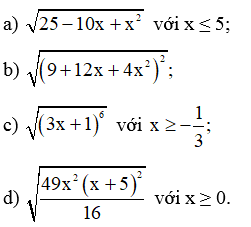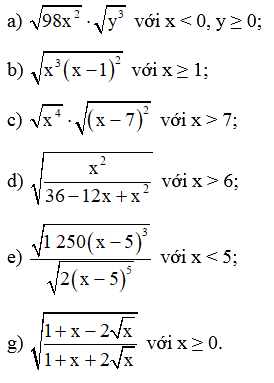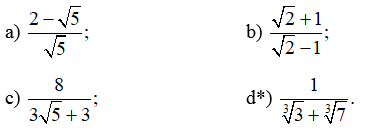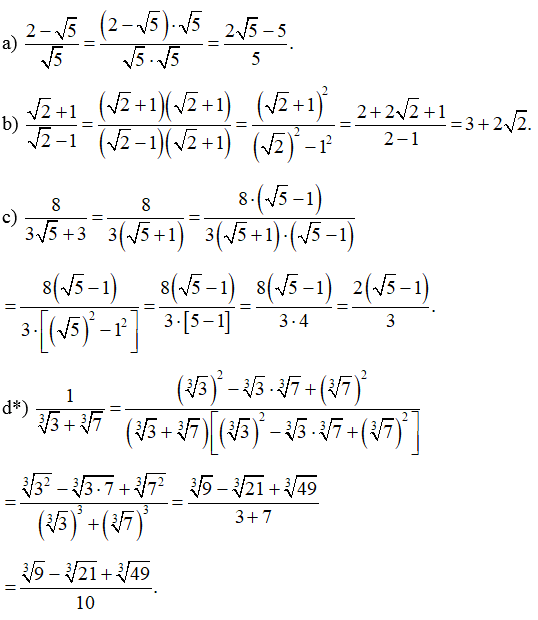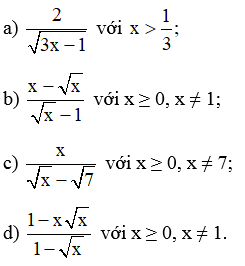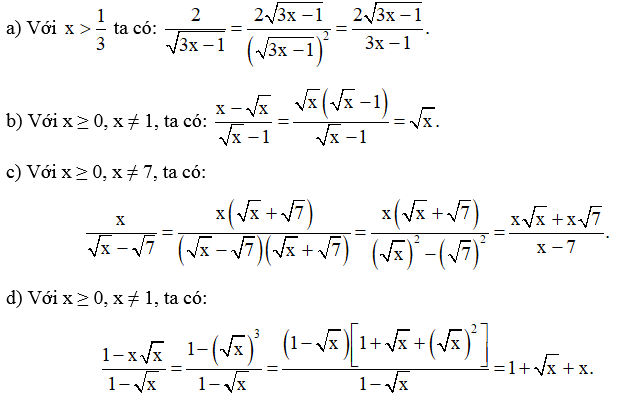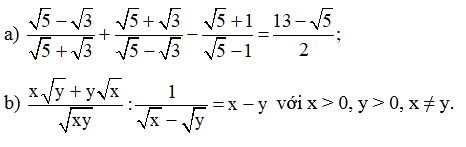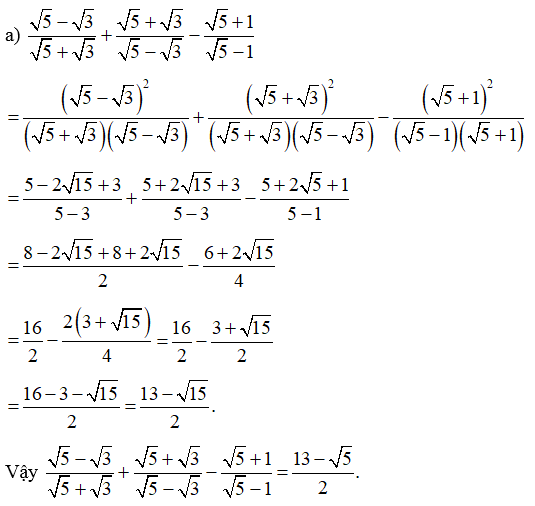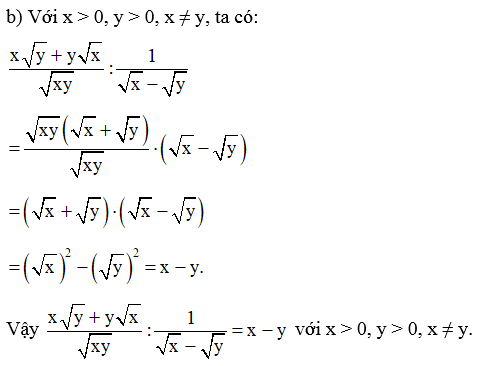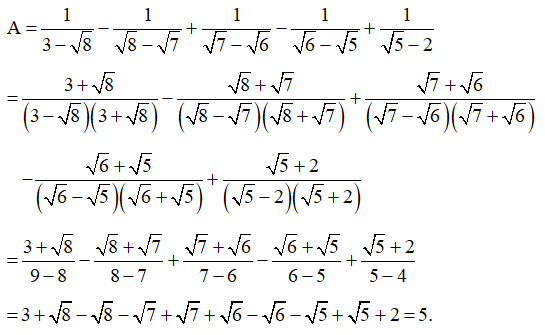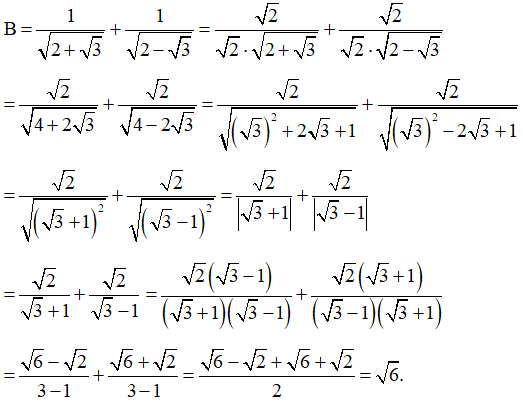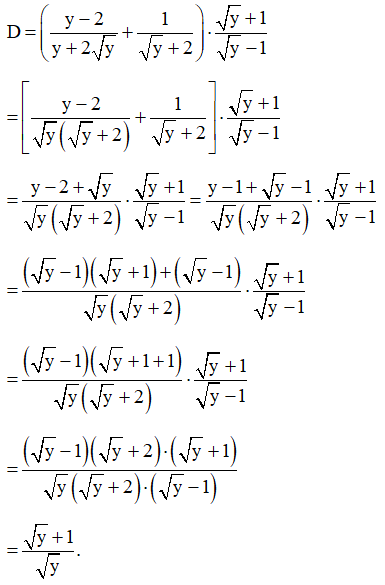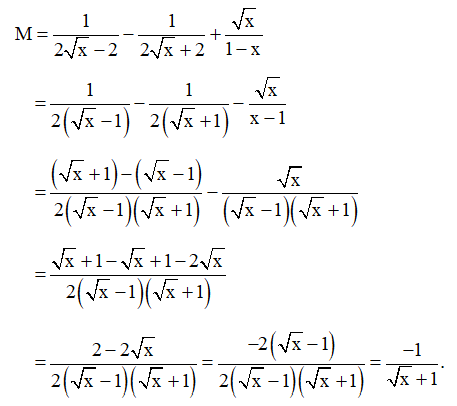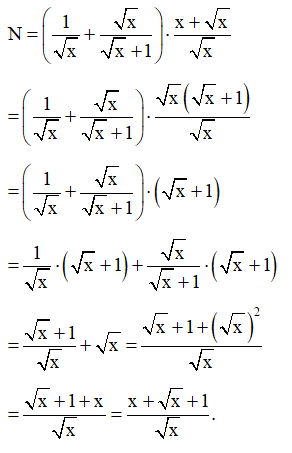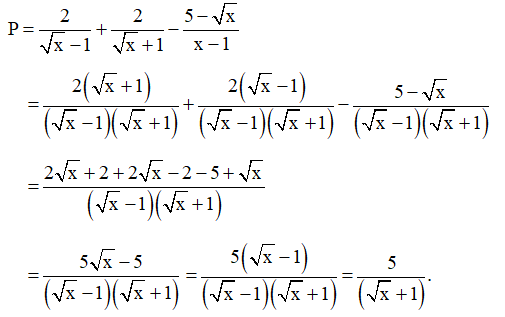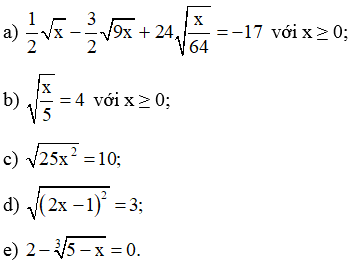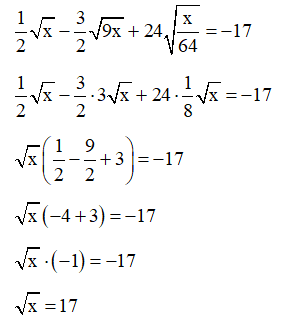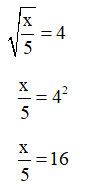Sách bài tập Toán 9 Bài 4 (Cánh diều): Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Giải SBT Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số - Cánh diều

Bài 31 trang 65 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một bình phương, hãy rút gọn biểu thức:

Lời giải:

a) $\sqrt{25-10x+x^2}=\sqrt{5^2-2\cdot 5x+x^2}=\sqrt{{\left(5-x\right)}^2}=\left|5-x\right|.$

Do x ≤ 5 nên 5 ‒ x ≥ 0, do đó |5 – x| = 5 – x.

Vậy $\sqrt{25-10x+x^2}=\left|5-x\right|=5-x.$

b) $\sqrt{{\left(9+12x+4x^2\right)}^2}=\left|9+12x+4x^2\right|$

= |(3 + 2x)²| = (3 + 2x)² (do 3 + 2x > 0 với mọi x).

c) $\sqrt{{\left(3x+1\right)}^6}=\sqrt{{\left[{\left(3x+1\right)}^3\right]}^2}=\left|{\left(3x+1\right)}^3\right|$

Do $x\ge -\frac{1}{3}$ nên 3x + 1 ≥ 0, do đó |(3x + 1)³| = (3x + 1)³.

Vậy $\sqrt{{\left(3x+1\right)}^6}=\left|{\left(3x+1\right)}^3\right|={\left(3x+1\right)}^3.$

d) $\sqrt{\frac{49x^2{\left(x+5\right)}^2}{16}}=\sqrt{{\left[\frac{7x\left(x+5\right)}{4}\right]}^2}=\left|\frac{7x\left(x+5\right)}{4}\right|.$

Do x ≥ 0 nên 7x(x + 5) > 0, do đó $\left|\frac{7x\left(x+5\right)}{4}\right|=\frac{7x\left(x+5\right)}{4}.$

Vậy $\sqrt{\frac{49x^2{\left(x+5\right)}^2}{16}}=\left|\frac{7x\left(x+5\right)}{4}\right|=\frac{7x\left(x+5\right)}{4}.$

Bài 32 trang 66 SBT Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một tích và một thương, hãy rút gọn biểu thức:

Lời giải:

a) $\sqrt{98x^2}\cdot \sqrt{y^3}=\sqrt{49\cdot 2\cdot x^2}\cdot \sqrt{y^2\cdot y}$

$=7\cdot \left|x\right|\cdot \sqrt{2}\cdot \left|y\right|\cdot \sqrt{y}$

$=-7xy\sqrt{2y}$ (do x < 0, y ≥ 0).

b) $\sqrt{x^3{\left(x-1\right)}^2}=\sqrt{x^2\cdot x\cdot {\left(x-1\right)}^2}=\left|x\right|\cdot \left|x-1\right|\cdot \sqrt{x}.$

Do x ≥ 1 nên x ‒ 1 ≥ 0, do đó |x – 1| = x – 1.

Vậy $\sqrt{x^3{\left(x-1\right)}^2}=\left|x\right|\cdot \left|x-1\right|\cdot \sqrt{x}=x\left(x-1\right)\sqrt{x}.$

c) $\sqrt{x^4}\cdot \sqrt{{\left(x-7\right)}^2}=\sqrt{{\left(x^2\right)}^2}\cdot \left|x-7\right|=\left|x^2\right|\cdot \left|x-7\right|=x^2\cdot \left|x-7\right|$ (do x² > 0 với mọi x > 7).

Do x > 7 nên x ‒ 7 > 0, do đó |x – 7| = x – 7.

Vậy $\sqrt{x^4}\cdot \sqrt{{\left(x-7\right)}^2}=x^2\cdot \left|x-7\right|=x^2\left(x-7\right).$

d) $\sqrt{\frac{x^2}{36-12x+x^2}}=\sqrt{\frac{x^2}{{\left(x-6\right)}^2}}=\sqrt{{\left(\frac{x}{x-6}\right)}^2}=\left|\frac{x}{x-6}\right|.$

Do x > 6 > 0 nên x ‒ 6 > 0, do đó $\frac{x}{x-6}>0,$ suy ra $\left|\frac{x}{x-6}\right|=\frac{x}{x-6}.$

Vậy $\sqrt{\frac{x^2}{36-12x+x^2}}=\left|\frac{x}{x-6}\right|=\frac{x}{x-6}.$

e) $\frac{\sqrt{1250{\left(x-5\right)}^3}}{\sqrt{2{\left(x-5\right)}^5}}=\sqrt{\frac{1250{\left(x-5\right)}^3}{2{\left(x-5\right)}^5}}$

$=\sqrt{\frac{625}{{\left(x-5\right)}^2}}=\sqrt{\frac{{25}^2}{{\left(x-5\right)}^2}}=\sqrt{{\left(\frac{25}{x-5}\right)}^2}=\left|\frac{25}{x-5}\right|.$

Do x < 5 nên x ‒ 5 < 0, do đó $\frac{25}{x-5}<0,$ suy ra $\left|\frac{25}{x-5}\right|=-\frac{25}{x-5}=\frac{25}{5-x}.$

Vậy $\frac{\sqrt{1250{\left(x-5\right)}^3}}{\sqrt{2{\left(x-5\right)}^5}}=\left|\frac{25}{x-5}\right|=\frac{25}{5-x}.$

g) $\sqrt{\frac{1+x-2\sqrt{x}}{1+x+2\sqrt{x}}}=\sqrt{\frac{{\left(\sqrt{x}-1\right)}^2}{{\left(\sqrt{x}+1\right)}^2}}=\sqrt{{\left(\frac{\sqrt{x}-1}{\sqrt{x}+1}\right)}^2}$

$=\left|\frac{\sqrt{x}-1}{\sqrt{x}+1}\right|=\frac{\left|\sqrt{x}-1\right|}{\sqrt{x}+1}$ (do $\sqrt{x}+1>0$ với mọi số thực x ≥ 0).

Bài 33 trang 66 SBT Toán 9 Tập 1: Trục căn thức ở mẫu:

Lời giải:

Bài 34 trang 66 SBT Toán 9 Tập 1: Trục căn thức ở mẫu:

Lời giải:

Bài 35 trang 66 SBT Toán 9 Tập 1: Chứng minh:

Lời giải:

Bài 36 trang 66 SBT Toán 9 Tập 1: a) Cho biểu thức:

$A=\frac{1}{3-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{7}}+\frac{1}{\sqrt{7}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{5}}+\frac{1}{\sqrt{5}-2}.$

Chứng minh: A = 5.

b*) Cho biểu thức: $B=\frac{1}{\sqrt{2+\sqrt{3}}}+\frac{1}{\sqrt{2-\sqrt{3}}}.$

Chứng minh: $B=\sqrt{6}.$

Lời giải:

a) Ta có:

Vậy A = 5.

b*) Ta có:

Vậy $B=\sqrt{6}.$

Bài 37 trang 67 SBT Toán 9 Tập 1: a) Cho biểu thức: $C=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}+\cdots +\frac{1}{\sqrt{24}}+\frac{1}{\sqrt{25}}.$

Chứng minh: $C>\frac{24}{5}.$

b*) Cho biểu thức: $D=\left(\frac{y-2}{y+2\sqrt{y}}+\frac{1}{\sqrt{y}+2}\right)\cdot \frac{\sqrt{y}+1}{\sqrt{y}-1}$ với y > 0, y ≠1.

Chứng minh: $D=\frac{\sqrt{y}+1}{\sqrt{y}}.$

Lời giải:

a) Do 2 < 3 < 4 < … < 24 < 25 nên $\sqrt{2}<\sqrt{3}<\sqrt{4}<\dots <\sqrt{24}<\sqrt{25}.$

Suy ra $\frac{1}{\sqrt{2}}>\frac{1}{\sqrt{3}}>\frac{1}{\sqrt{4}}>\cdots >\frac{1}{\sqrt{24}}>\frac{1}{\sqrt{25}}.$

Do đó

$\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{4}}+\cdots +\frac{1}{\sqrt{24}}+\frac{1}{\sqrt{25}}>\underset{\text{gom }24\text{ so hang }\frac{1}{\sqrt{25}}}{\underbrace{\frac{1}{\sqrt{25}}+\frac{1}{\sqrt{25}}+\frac{1}{\sqrt{25}}+\cdots +\frac{1}{\sqrt{25}}+\frac{1}{\sqrt{25}}}}\text{. }$

Vậy $C>24\cdot \frac{1}{\sqrt{25}}$ hay $C>\frac{24}{5}.$

b*) Với y > 0, y ≠1, ta có:

Vậy với y > 0, y ≠1 thì $D=\frac{\sqrt{y}+1}{\sqrt{y}}.$

Bài 38 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $M=\frac{1}{2\sqrt{x}-2}-\frac{1}{2\sqrt{x}+2}+\frac{\sqrt{x}}{1-x}$ với x ≥ 0, x ≠ 1.

a) Rút gọn biểu thức M.

b) Tính giá trị của biểu thức M tại $x=\frac{4}{9}.$

c*) Tìm giá trị của x để $\left|M\right|=\frac{1}{3}.$

Lời giải:

a) Với x ≥ 0, x ≠ 1, ta có:

Vậy với x ≥ 0, x ≠ 1 thì $M=\frac{-1}{\sqrt{x}+1}.$

b) Thay $x=\frac{4}{9}$ (thỏa mãn điều kiện) vào biểu thức $M=\frac{-1}{\sqrt{x}+1},$ ta có:

$M=\frac{-1}{\sqrt{\frac{4}{9}}+1}=\frac{-1}{\frac{2}{3}+1}=\frac{-1}{\frac{5}{3}}=\frac{-3}{5}.$

Vậy giá trị của biểu thức M tại $x=\frac{4}{9}$ là $\frac{-3}{5}$

c*) Với x ≥ 0, x ≠ 1, để $\left|M\right|=\frac{1}{3}$ thì $\left|\frac{-1}{\sqrt{x}+1}\right|=\frac{1}{3}.$

Suy ra $\frac{1}{\sqrt{x}+1}=\frac{1}{3}$ (do $\sqrt{x}+1>0)$ nên $\sqrt{x}+1=3$

Do đó $\sqrt{x}=2,$ suy ra x = 4 (thoả mãn x ≥ 0, x ≠ 1).

Vậy x = 4 thì $\left|M\right|=\frac{1}{3}.$

Bài 39 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $N=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right)\cdot \frac{x+\sqrt{x}}{\sqrt{x}}$ với x > 0.

a) Rút gọn biểu thức N.

b*) Tìm giá trị nhỏ nhất của N.

Lời giải:

a) Với x > 0, ta có:

Vậy với x > 0 thì $N=\frac{x+\sqrt{x}+1}{\sqrt{x}}.$

b*) Với x > 0, ta có: $N=\frac{x+\sqrt{x}+1}{\sqrt{x}}=\sqrt{x}+1+\frac{1}{\sqrt{x}}$.

Do $\sqrt{x}>0$ và $\frac{1}{\sqrt{x}}>0$ với x > 0 nên theo kết quả Ví dụ 5 (trang 65), SBT Toán 9, Tập một, ta có: $\sqrt{x}+\frac{1}{\sqrt{x}}\ge 2\sqrt{\sqrt{x}\cdot \frac{1}{\sqrt{x}}}$ hay $\sqrt{x}+\frac{1}{\sqrt{x}}\ge 2,$ suy ra $\sqrt{x}+\frac{1}{\sqrt{x}}+1\ge 2+1$ hay N ≥ 3.

Vậy giá trị nhỏ nhất của N là 3 khi $\sqrt{x}=\frac{1}{\sqrt{x}}$ hay x = 1 (thoả mãn x > 0).

Bài 40 trang 67 SBT Toán 9 Tập 1: Cho biểu thức: $P=\frac{2}{\sqrt{x}-1}+\frac{2}{\sqrt{x}+1}-\frac{5-\sqrt{x}}{x-1}$ với x ≥ 0, x ≠ 1.

a) Rút gọn biểu thức P.

b) Tính giá trị của biểu thức P tại x = 4.

c*) Tìm giá trị của x để P có giá trị là số nguyên.

Lời giải:

a) Với x ≥ 0, x ≠ 1, ta có:

Vậy với x ≥ 0, x ≠ 1 thì $P=\frac{5}{\sqrt{x}+1}.$

b) Thay x = 4 (thỏa mãn điều kiện) vào biểu thức $P=\frac{5}{\sqrt{x}+1},$ ta có:

$P=\frac{5}{\sqrt{4}+1}=\frac{5}{2+1}=\frac{5}{3}.$

Vậy giá trị của biểu thức P tại x = 4 là $\frac{5}{3}$

c*) Với x ≥ 0, x ≠ 1, ta có $\sqrt{x}+1\ge 1$ nên $\frac{5}{\sqrt{x}+1}>0$ và $\frac{5}{\sqrt{x}+1}\le 5.$

Do đó 0 < P ≤ 5.

Vì vậy, để P có giá trị là số nguyên thì P ∈{1; 2; 3; 4; 5}.

⦁ Nếu P = 1 thì $\frac{5}{\sqrt{x}+1}=1,$ suy ra $\sqrt{x}+1=5$ hay $\sqrt{x}=4,$ do đó x = 4² hay x = 16 (thoả mãn x ≥ 0, x ≠ 1).

⦁ Nếu P = 2 thì $\frac{5}{\sqrt{x}+1}=2,$ suy ra $\sqrt{x}+1=\frac{5}{2}$ hay $\sqrt{x}=\frac{3}{2},$ do đó $x={\left(\frac{3}{2}\right)}^2$ hay $x=\frac{9}{4}$ (thoả mãn x ≥ 0, x ≠ 1).

⦁ Nếu P = 3 thì $\frac{5}{\sqrt{x}+1}=3,$ suy ra $\sqrt{x}+1=\frac{5}{3}$ hay $\sqrt{x}=\frac{2}{3},$$x={\left(\frac{2}{3}\right)}^2$ hay $x=\frac{4}{9}$ (thoả mãn x ≥ 0, x ≠ 1).

⦁ Nếu P = 4 thì $\frac{5}{\sqrt{x}+1}=4,$ suy ra $\sqrt{x}+1=\frac{5}{4}$ hay $\sqrt{x}=\frac{1}{4},$ do đó $x={\left(\frac{1}{4}\right)}^2$ hay $x=\frac{1}{16}$ (thoả mãn x ≥ 0, x ≠ 1).

⦁ Nếu P = 5 thì $\frac{5}{\sqrt{x}+1}=5,$ suy ra $\sqrt{x}+1=1$ hay $\sqrt{x}=0,$ do đó x = 0 (thoả mãn x ≥ 0, x ≠ 1).

Vậy $x\in \left\{16;\frac{9}{4};\frac{4}{9};\frac{1}{16};0\right\}$ thì P có giá trị là số nguyên.

Bài 41 trang 67 SBT Toán 9 Tập 1: Tìm x, biết:

Lời giải:

a) Với x ≥ 0, ta có:

x = 17² = 289 (thỏa mãn x ≥ 0).

Vậy x = 289.

b) Với x ≥ 0, ta có:

x = 80 (thỏa mãn x ≥ 0).

Vậy x = 80.

c) $\sqrt{25x^2}=10$

$\sqrt{{\left(5x\right)}^2}=10$

|5x| = 10

5x = 10 hoặc 5x = ‒10

x = 2 hoặc x= ‒2.

Vậy x = 2 hoặc x = ‒2.

d) $\sqrt{{\left(2x-1\right)}^2}=3$

|2x – 1| = 3

Trường hợp 1: 2x ‒ 1 = 3

2x = 4

x = 2.

Trường hợp 2: 2x ‒ 1 = ‒3

2x = ‒2

x = ‒1.

Vậy x = 2 hoặc x = ‒1.

e) $2-\sqrt[3]{5-x}=0.$

$\sqrt[3]{5-x}=2$

5 ‒ x = 2³

5 – x = 8

x = ‒3.

Vậy x = ‒3.

Xem thêm Lời giải bài tập Toán 9 sách Cánh diều hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Tỉ số lượng giác của góc nhọn

Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 3: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài tập cuối chương 4