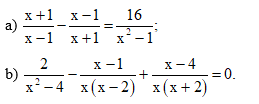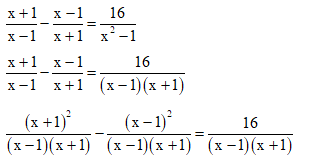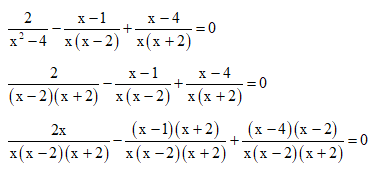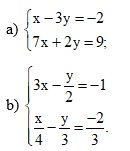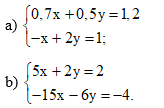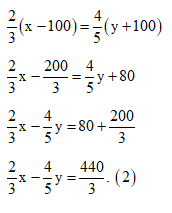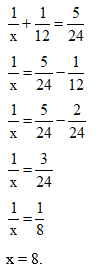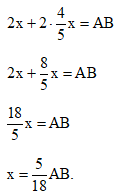Sách bài tập Toán 9 (Cánh diều): Bài tập cuối chương 1

Giải SBT Toán 9 Bài tập cuối chương 1 - Cánh diều

Bài 26 trang 21 SBT Toán 9 Tập 1: Tổng các nghiệm của phương trình (x ‒ 3)(2x + 6) = 0 là

A. ‒6.

B. 0.

C. 3.

D. 6.

Lời giải:

Đáp án đúng là: B

Giải phương trình:

(x ‒ 3)(2x + 6) = 0

x ‒ 3 = 0 hoặc 2x + 6 = 0

x = 3 hoặc 2x = ‒6

x = 3 hoặc x = ‒3.

Do đó, phương trình đã cho có hai nghiệm là x = 3 và x = ‒3.

Vậy tổng hai nghiệm của phương trình là: 3 + (‒3) = 0.

Bài 27 trang 21 SBT Toán 9 Tập 1: Trong các cặp số (‒1; 0), (2; ‒2), (6; ‒1), (4; ‒3), $\left(0;\frac{-3}{5}\right),$ có bao nhiêu cặp số là nghiệm của phương trình 3x + 5y = ‒3?

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải:

Đáp án đúng là: C

Phương trình: 3x + 5y = ‒3 (1)

Thay x = ‒1 và y = 0 vào phương trình (1) ta có: 3.(‒1) + 5.0 = ‒3;

Thay x = 2 và y = ‒2 vào phương trình (1) ta có: 3.2 + 5.(‒2) = ‒4 ≠ ‒3;

Thay x = 6 và y = ‒1 vào phương trình (1) ta có: 3.6 + 5.(‒1) = 13 ≠ ‒3;

Thay x = 4 và y = ‒3 vào phương trình (1) ta có: 3.4 + 5.(‒3) = ‒3;

Thay x = 0 và $y=-\frac{3}{5}$ vào phương trình (1) ta có: $3\cdot 0+5\cdot \left(-\frac{3}{5}\right)=-3.$

Vậy có 3 cặp số là nghiệm của phương trình 3x + 5y = ‒3, đó là các cặp số (‒1; 0), (4; ‒3), $\left(0;\frac{-3}{5}\right).$

Bài 28 trang 21 SBT Toán 9 Tập 1: Giải các phương trình sau:

Lời giải:

a) Điều kiện xác định: x ≠ 1 và x ≠ ‒1.

(x + 1)² – (x – 1)² = 16

x² + 2x + 1 ‒ (x² ‒ 2x + 1) = 16

x² + 2x + 1 ‒ x² + 2x ‒ 1 = 16

4x = 16

x = 4.

Ta thấy x = 4 thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho có nghiệm x = 4.

b) Điều kiện xác định: x ≠ 0, x ≠ 2 và x ≠ ‒2.

2x – (x – 1)(x + 2) + (x – 4)(x – 2) = 0

2x ‒ (x² + 2x – x ‒ 2) + (x² ‒ 2x ‒ 4x + 8) = 0

2x – (x² + x – 2) + (x² – 6x + 8) = 0

2x ‒ x² ‒ x + 2 + x² ‒ 6x + 8 = 0

‒5x + 10 = 0

‒5x = ‒10

x = 2.

Ta thấy x = 2 không thỏa mãn điều kiện xác định của phương trình.

Vậy phương trình đã cho vô nghiệm.

Bài 29 trang 22 SBT Toán 9 Tập 1: Giải các hệ phương trình sau bằng phương pháp thế:

Lời giải:

a) $\left\{\begin{array}{l}x-3y=-2\left(1a\right)\\ 7x+2y=9\left(2a\right)\end{array}\right.$

Từ phương trình (1a), ta có: x = 3y – 2. (3a)

Thế vào phương trình (2a) ta được: 7.(3y – 2) + 2y = 9. (4a)

Giải phương trình (4a):

7.(3y – 2) + 2y = 9

21y ‒ 14 + 2y = 9

23y = 23

y = 1.

Thay y = 1 vào phương trình (3a), ta có: x = 3.1 – 2 = 1.

Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (1; 1).

b) $\left\{\begin{array}{l}3x-\frac{y}{2}=-1\left(1b\right)\\ \frac{x}{4}-\frac{y}{3}=\frac{-2}{3}\left(2b\right)\end{array}\right.$

Từ phương trình (1b), ta có:

$3x=\frac{y}{2}-1,$ suy ra $x=\frac{y}{6}-\frac{1}{3}$ hay $x=\frac{y-2}{6}.\left(3b\right)$

Thế vào phương trình (2b) ta được:

$\frac{x}{4}-\frac{y}{3}=\frac{-2}{3}$$\frac{\frac{y-2}{6}}{4}-\frac{y}{3}=\frac{-2}{3},$ hay$\frac{y-2}{24}-\frac{y}{3}=\frac{-2}{3}.\left(4b\right)$

Giải phương trình (4b):

$\frac{y-2}{24}-\frac{y}{3}=\frac{-2}{3}$

$\frac{y-2}{24}-\frac{8y}{24}=\frac{-2\cdot 8}{24}$

y – 2 – 8y = –2.8

y – 2 – 8y = –16

–7y = –14

y = 2.

Thay y = 2 vào phương trình (3b) ta có: $x=\frac{2-2}{6}=0.$

Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (0; 2).

Bài 30 trang 22 SBT Toán 9 Tập 1: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

Lời giải:

a) $\left\{\begin{array}{l}0,7x+0,5y=1,2\left(1a\right)\\ -x+2y=1\left(2a\right)\end{array}\right.$

Nhân hai vế của phương trình (1a) với 4, ta được hệ phương trình sau: $\left\{\begin{array}{l}2,8x+2y=4,8\left(3a\right)\\ -x+2y=1\left(2a\right)\end{array}\right.$

Trừ từng vế hai phương trình (3a) và (2a), ta nhận được phương trình:

3,8x = 3,8, suy ra x = 1.

Thay x = 1 vào phương trình (2a) ta có: ‒1 + 2y = 1. (4a)

Giải phương trình (4a):

‒1 + 2y = 1

2y = 2

y = 1.

Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (1; 1).

b) $\left\{\begin{array}{l}5x+2y=2\left(1b\right)\\ -15x-6y=-4\left(2b\right)\end{array}\right.$

Nhân hai vế của phương trình (1b) với 3, ta được hệ phương trình sau: $\left\{\begin{array}{l}15x+6y=6\left(3b\right)\\ -15x-6y=-4\left(2b\right)\end{array}\right.$

Cộng từng vế hai phương trình (3b) và (2b), ta nhận được phương trình:

0x + 0y = 2.

Phương trình trên vô nghiệm.

Vậy hệ phương trình đã cho vô nghiệm.

Bài 31 trang 22 SBT Toán 9 Tập 1: Hai khu công nghiệp A và B có tổng cộng 2 200 công nhân. Sau khi chuyển 100 công nhân ở khu A sang khu B thì $\frac{2}{3}$ số công nhân ở khu A bằng $\frac{4}{5}$ số công nhân ở khu B. Tính số công nhân ở mỗi khu công nghiệp lúc ban đầu.

Lời giải:

Gọi x, y (công nhân) lần lượt là số công nhân ở khu công nghiệp A, khu công nghiệp B lúc ban đầu với x, y ∈ ℕ*.

Theo bài, hai khu công nghiệp A và B có tổng cộng 2 200 công nhân nên ta có phương trình: x + y = 2 200. (1)

Khi chuyển 100 công nhân ở khu A sang khu B thì:

⦁ số công nhân ở khu A lúc này là x – 100 (công nhân), do đó $\frac{2}{3}$ số công nhân ở khu A là $\frac{2}{3}\left(x-100\right)$ (công nhân).

⦁ số công nhân ở khu B lúc này là y + 100 (công nhân), do đó $\frac{4}{5}$ số công nhân ở khu B là $\frac{4}{5}\left(y+100\right)$ (công nhân).

Theo bài, sau khi chuyển 100 công nhân ở khu A sang khu B thì $\frac{2}{3}$ số công nhân ở khu A bằng $\frac{4}{5}$ số công nhân ở khu B nên ta có phương trình:

Từ (1) và (2), ta có hệ phương trình: $\left\{\begin{array}{l}x+y=2200\left(1\right)\\ \frac{2}{3}x-\frac{4}{5}y=\frac{440}{3}\left(2\right)\end{array}\right.$

Nhân hai vế của phương trình (1) với 2 và nhân hai vế của phương trình (2) với 3, ta được hệ phương trình sau: $\left\{\begin{array}{l}2x+2y=4400\left(3\right)\\ 2x-\frac{12}{5}y=440\left(4\right)\end{array}\right.$

Trừ từng vế hai phương trình (3) và (4), ta nhận được phương trình:

$\frac{22}{5}y=3960$ hay y = 900.

Thay y = 900 vào phương trình (1) ta có: x + 900 = 2 200 hay x = 1 300.

Ta thấy x = 1 300, y = 900 thỏa mãn điều kiện.

Vậy số công nhân ở khu công nghiệp A và khu công nghiệp B lúc ban đầu lần lượt là 1 300 công nhân và 900 công nhân.

Bài 32 trang 22 SBT Toán 9 Tập 1: Một công ty du lịch tiến hành giảm giá cho gói du lịch loại A trong các dịp lễ:

– Tuần lễ kích cầu du lịch: Hà Nội đi Đà Lạt giảm 15% giá niêm yết, Hà Nội đi Huế giảm 10% giá niêm yết;

– Ngày lễ Quốc tế Lao động: Hà Nội đi Đà Lạt giảm 20% giá niêm yết, Hà Nội đi Huế giảm 15% giá niêm yết.

Trong tuần lễ kích cầu du lịch, nếu 3 gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt và 2 gói du lịch loại A cho chuyến Hà Nội đi Huế thì khách hàng phải trả 15 000 000 đồng. Trong ngày lễ Quốc tế Lao động, nếu 2 gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt và 3 gói du lịch loại A cho chuyến Hà Nội đi Huế thì khách hàng phải trả 14 810 000 đồng. Tính giá niêm yết của gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt và chuyến Hà Nội đi Huế.

Lời giải:

Đổi 15 000 000 đồng = 15 triệu đồng; 14 810 000 đồng = 14,81 triệu đồng.

Gọi x (triệu đồng), y (triệu đồng) lần lượt là giá niêm yết của gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt, chuyến Hà Nội đi Huế với x > 0, y > 0.

– Trong tuần lễ kích cầu du lịch:

⦁ 1 gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt có giá là:

x.(100% – 15%) = x.85% = 0,85x (đồng);

⦁ 1 gói du lịch loại A cho chuyến Hà Nội đi Huế có giá là:

y.(100% – 10%) = y.90% = 0,9y (đồng).

– Trong ngày lễ Quốc tế Lao động:

⦁ 1 gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt có giá là:

x.(100% – 20%) = x.80% = 0,8x (đồng);

⦁ 1 gói du lịch loại A cho chuyến Hà Nội đi Huế có giá là:

y.(100% – 15%) = y.85% = 0,85y (đồng).

Như vậy:

⦁ Trong tuần lễ kích cầu du lịch, 3 gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt và 2 gói du lịch loại A cho chuyến Hà Nội đi Huế phải trả số tiền là:

3.0,85x + 2.0,9y = 2,55x + 1,8y (đồng).

⦁ Trong ngày lễ Quốc tế Lao động, 2 gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt và 3 gói du lịch loại A cho chuyến Hà Nội đi Huế phải trả số tiền là:

2.0,8x + 3.0,85y = 1,6x + 2,55y (đồng).

Ta lập được hệ phương trình: $\left\{\begin{array}{l}2,55x+1,8y=15\left(1\right)\\ 1,6x+2,55y=14,81\left(2\right)\end{array}\right.$

Nhân hai vế của phương trình (1) với 1,6 và nhân hai vế của phương trình (2) với 2,55, ta được hệ phương trình sau: $\left\{\begin{array}{l}4,08x+2,88y=24\left(3\right)\\ 4,08x+6,5025y=37,7655\left(4\right)\end{array}\right.$

Trừ từng vế hai phương trình (4) và (3), ta nhận được phương trình:

3,6225y = 13,7655 hay y = 3,8.

Thay y = 3,8 vào phương trình (1) ta có: 2,55x + 1,8.3,8 = 15. (5)

Giải phương trình (5):

2,55x + 1,8.3,8 = 15

2,55x + 6,84 = 15

2,55x = 8,16

x = 3,2.

Ta thấy x = 3,2 và y = 3,8 thỏa mãn điều kiện.

Vậy giá niêm yết của gói du lịch loại A cho chuyến Hà Nội đi Đà Lạt và chuyến Hà Nội đi Huế lần lượt là 3,2 triệu đồng và 3,8 triệu đồng.

Bài 33 trang 22 SBT Toán 9 Tập 1: Một tam giác có chiều cao bằng $\frac{3}{4}$ cạnh đáy. Nếu tăng chiều cao thêm 3 dm và giảm cạnh đáy đi 3 dm thì diện tích của tam giác tăng thêm 6 dm². Tính chiều cao và cạnh đáy của tam giác đó.

Lời giải:

Gọi x (dm), y (dm) lần lượt là chiều cao và độ dài cạnh đáy của tam giác với x > 0; y > 3.

Theo bài, tam giác có chiều cao bằng $\frac{3}{4}$ cạnh đáy nên $x=\frac{3}{4}y.\left(1\right)$

Diện tích tam giác là: $\frac{xy}{2}$ (dm²).

Chiều cao của tam giác khi tăng thêm 3 dm là: x + 3 (dm).

Cạnh đáy của tam giác khi giảm đi 3 dm là: y – 3 (dm).

Diện tích tam giác lúc này là: $\frac{\left(x+3\right)\left(y-3\right)}{2}$ (dm²).

Theo bài, nếu tăng chiều cao thêm 3 dm và giảm cạnh đáy đi 3 dm thì diện tích của tam giác tăng thêm 6 dm² nên ta có phương trình:

$\frac{\left(x+3\right)\left(y-3\right)}{2}=\frac{xy}{2}+6$

(x + 3)(y – 3) = xy + 12

xy – 3x + 3y – 9 = xy + 12

xy – 3x + 3y – xy = 12 + 9

– 3x + 3y = 21

–x + y = 7. (2)

Từ (1) và (2), ta có hệ phương trình: $\left\{\begin{array}{l}x=\frac{3}{4}y\left(1\right)\\ –x+y=7\left(2\right)\end{array}\right.$

Thế vào phương trình (2) ta có: $-\frac{3}{4}y+y=7\left(3\right)$

Giải phương trình (3):

$-\frac{3}{4}y+y=7$

$\frac{1}{4}y=7$

y = 28.

Thay y = 28 vào phương trình (1) ta có: $x=\frac{3}{4}\cdot 28=21.$

Ta thấy x = 21 và y = 28 thỏa mãn điều kiện.

Vậy tam giác đó có chiều cao là 21 dm, cạnh đáy là 28 dm.

Bài 34 trang 22 SBT Toán 9 Tập 1: Hai vòi nước cùng chảy vào một bể không chứa nước thì bể đó đầy nước sau 4 giờ 48 phút. Nếu vòi thứ nhất chảy trong 4 giờ và vòi thứ hai chảy trong 3 giờ thì cả hai vòi chảy được $\frac{3}{4}$ bể nước. Tính thời gian để mỗi vòi chảy riêng một mình đầy bể.

Lời giải:

Đổi 4 giờ 48 phút = 4,8 giờ.

Gọi x (giờ), y (giờ) lần lượt là thời gian vòi thứ nhất và vòi thứ hai chảy một mình được đầy bể (điều kiện x > 4,8 và y > 4,8).

⦁ Trong 1 giờ, vòi thứ nhất chảy một mình được $\frac{1}{x}$ (bể), vòi thứ hai chảy một mình được $\frac{1}{y}$ (bể).

Hai vòi nước cùng chảy vào một bể sau 4 giờ 48 phút giờ sẽ đầy, nên trong 1 giờ hai vòi cùng chảy thì được $\frac{1}{4,8}=\frac{5}{24}$ bể, ta có phương trình:

$\frac{1}{x}+\frac{1}{y}=\frac{5}{24}\left(1\right)$

⦁ Trong 4 giờ vòi thứ nhất chảy một mình được $\frac{4}{x}$ (bể).

Trong 3 giờ vòi thứ hai chảy một mình được $\frac{3}{y}$ (bể).

Theo bài, nếu vòi thứ nhất chảy trong 4 giờ, vòi thứ hai chảy trong 3 giờ thì cả hai vòi chảy được $\frac{3}{4}$ bể nên ta có phương trình: $\frac{4}{x}+\frac{3}{y}=\frac{3}{4}\left(2\right)$

Từ (1) và (2) ta có hệ phương trình: $\left\{\begin{array}{l}\frac{1}{x}+\frac{1}{y}=\frac{5}{24}\left(1\right)\\ \frac{4}{x}+\frac{3}{y}=\frac{3}{4}\left(2\right)\end{array}\right.$

Nhân hai vế của phương trình (1) với 4, ta được hệ phương trình sau: $\left\{\begin{array}{l}\frac{4}{x}+\frac{4}{y}=\frac{5}{6}\left(3\right)\\ \frac{4}{x}+\frac{3}{y}=\frac{3}{4}\left(2\right)\end{array}\right.$

Trừ từng vế của phương trình (3) và (2), ta nhận được phương trình sau:

$\frac{1}{y}=\frac{1}{12}$ nên y = 12.

Thay y = 12 vào phương trình (1), ta được: $\frac{1}{x}+\frac{1}{12}=\frac{5}{24}.\left(4\right)$

Giải phương trình (4):

Ta thấy x = 8 và y = 12 thỏa mãn điều kiện.

Vậy thời gian chảy riêng một mình để đầy bể của vòi thứ nhất và vòi thứ hai lần lượt là 8 giờ và 12 giờ.

Bài 35 trang 23 SBT Toán 9 Tập 1: Hai xe máy khởi hành cùng một lúc. Xe máy thứ nhất đi từ địa điểm A đến địa điểm B và xe máy thứ hai đi từ địa điểm B đến địa điểm A (trên cùng quãng đường). Tốc độ của xe máy thứ hai bằng $\frac{4}{5}$ tốc độ của xe máy thứ nhất và sau 2 giờ hai xe gặp nhau. Hỏi mỗi xe đi cả quãng đường AB trong bao lâu?

Lời giải:

Gọi x (km/h), y (km/h) lần lượt là tốc độ của xe máy thứ nhất, xe máy thứ hai với x > 0, y > 0.

Theo bài, tốc độ của xe máy thứ hai bằng $\frac{4}{5}$ tốc độ của xe máy thứ nhất nên ta có phương trình: $y=\frac{4}{5}x.$

Sau 2 giờ, xe máy thứ nhất đi được quãng đường là: 2x (km) và xe máy thứ hai đi được quãng đường là: 2y (km).

Vì sau 2 giờ hai xe gặp nhau nên ta có:

2x + 2y = AB (trong đó AB là độ dài quãng đường AB).

Ta lập được hệ phương trình: $\left\{\begin{array}{l}y=\frac{4}{5}x\left(1\right)\\ 2x+2y=AB\left(2\right)\end{array}\right.$

Thế (1) vào phương trình (2), ta nhận được phương trình:

p>Thay $x=\frac{5}{18}AB$ vào phương trình (1), ta được:

$y=\frac{4}{5}\cdot \frac{5}{18}AB=\frac{2}{9}AB.$

Như vậy, xe máy thứ nhất đi cả quãng đường AB trong: $AB:\left(\frac{5}{18}AB\right)=\frac{18}{5}=3,6$ (giờ); xe máy thứ hai đi cả quãng đường AB trong: $AB:\left(\frac{2}{9}AB\right)=\frac{9}{2}=4,5$(giờ)

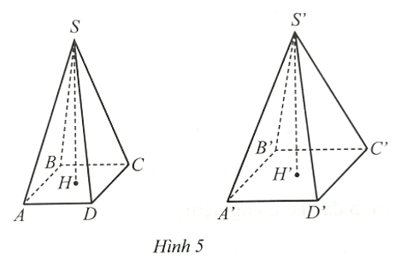
Bài 36 trang 23 SBT Toán 9 Tập 1: Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S.A’B’C’D’ có cùng chiều cao SH = S’H’ = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S.A’B’C’D’ là 240 cm³. Tính độ dài cạnh đáy của mỗi hình chóp, biết rằng A’B’ ‒ AB = 2 cm.

Lời giải:

Đặt AB = x (cm) và A’B = y (cm) với x > 0 và y > 0.

Theo bài, A’B’ ‒ AB = 2 cm nên ta có: y – x = 2. (1)

Diện tích đáy của hình chóp tứ giác đều S.ABCD là:

S_ABCD = AB² = x² (cm²).

Thể tích của hình chóp tứ giác đều S.ABCD là:

$\frac{1}{3}\cdot SH\cdot S_{ABCD}=\frac{1}{3}\cdot 30\cdot x^2=10x^2$ (cm³).

Diện tích đáy của hình chóp tứ giác đều S.A’B’C’D’ là:

S_{A’B’C’D’} = A’B’² = y² (cm²).

Thể tích của hình chóp tứ giác đều S.A’B’C’D’ là:

$\frac{1}{3}\cdot S^{\text{'}}{H}^{\text{'}}\cdot S_{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}=\frac{1}{3}\cdot 30\cdot y^2=10y^2$ (cm³).

Theo bài, thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S.A’B’C’D’ là 240 cm³ nên ta có phương trình:

10y² – 10x² = 240

y² – x² = 24

(y – x)(y + x) = 24

2.(y + x) = 24 (do y – x = 2)

y + x = 12. (2)

Từ (1) và (2) ta có hệ phương trình: $\left\{\begin{array}{l}y-x=2\left(1\right)\\ y+x=12\left(2\right)\end{array}\right.$

Cộng từng vế hai phương trình (1) và (20, ta nhận được phương trình:

2y = 14, suy ra y = 7.

Thay y = 7 vào phương trình (1), ta có: 7 – x = 2, suy ra x = 7 – 2 = 5.

Ta thấy x = 5 và y = 7 thỏa mãn điều kiện.

Vậy độ dài cạnh đáy của hình chóp S.ABCD và S’.A’B’C’D’ lần lượt là 5 cm và 7 cm.

Xem thêm Lời giải bài tập Toán 9 sách Cánh diều hay, chi tiết khác:

Bài 1: Bất đẳng thức

Bài 2: Bất phương trình bậc nhất một ẩn

Bài tập cuối chương 2

Bài 1: Căn bậc hai và căn bậc ba của số thực

Bài 2: Một số phép tính về căn bậc hai của số thực