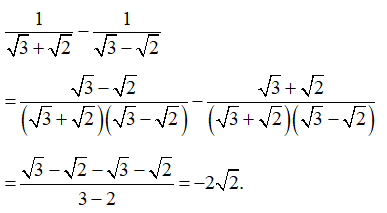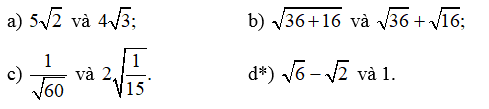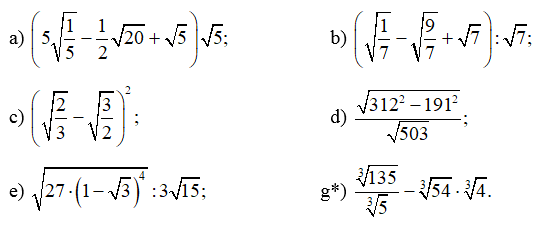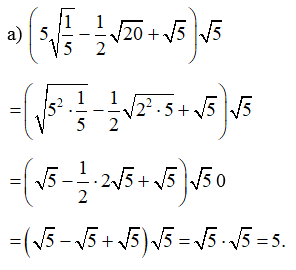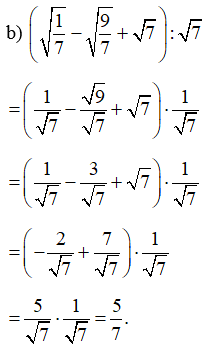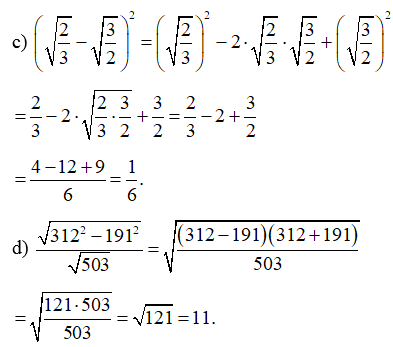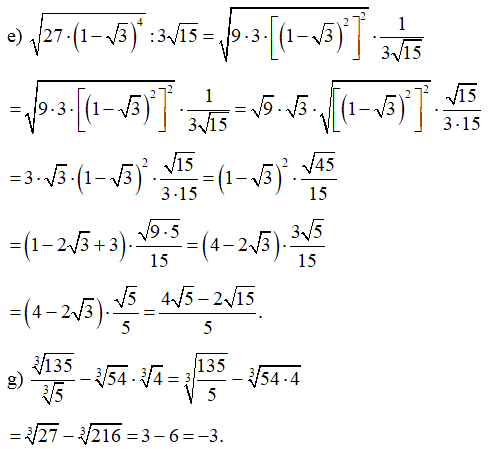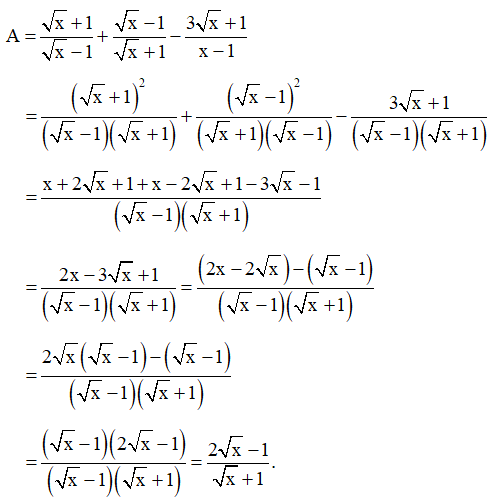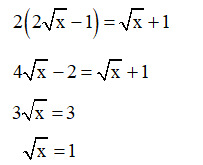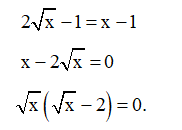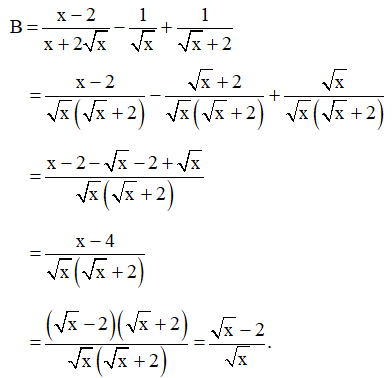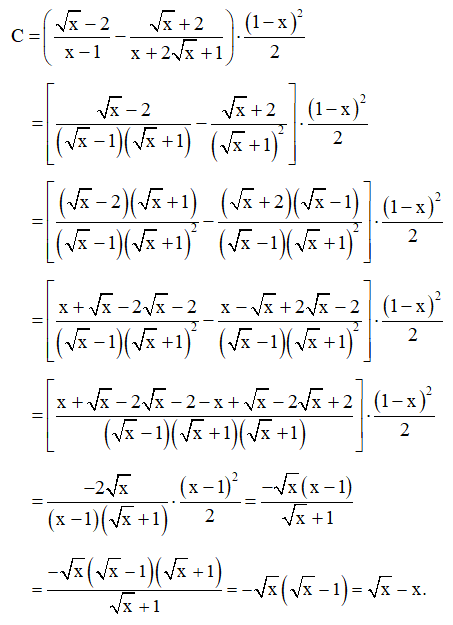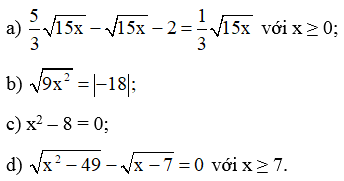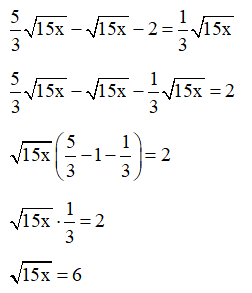Sách bài tập Toán 9 (Cánh diều): Bài tập cuối chương 3

Giải SBT Toán 9 Bài tập cuối chương 3 - Cánh diều

Bài 42 trang 68 SBT Toán 9 Tập 1: Đưa thừa số vào dấu căn bậc hai của $3\sqrt{5}$ ta được

A. $\sqrt{15}$

B. 15.

C. $\sqrt{45}$

D. 45.

Lời giải:

Đáp án đúng là: C

Ta có: $3\sqrt{5}=\sqrt{3^2\cdot 5}=\sqrt{9\cdot 5}=\sqrt{45}.$

Bài 43 trang 68 SBT Toán 9 Tập 1: Giá trị của biểu thức $\frac{1}{\sqrt{3}+\sqrt{2}}-\frac{1}{\sqrt{3}-\sqrt{2}}$ bằng

A. 0.

B. 4.

C. $2\sqrt{2}.$

D. $-2\sqrt{2}.$

Lời giải:

Đáp án đúng là: D

Ta có:

Bài 44 trang 68 SBT Toán 9 Tập 1: Nếu x³ = –2 thì x bằng

A. –8.

B. $\sqrt{2}.$

C. $-\sqrt[3]{2}.$

D. $\sqrt[3]{2}.$

Lời giải:

Đáp án đúng là: C

Ta có:

x³ = –2

$\sqrt[3]{x^3}=\sqrt[3]{-2}$

$x=\sqrt[3]{-2}.$

Vậy $x=\sqrt[3]{-2}.$

Bài 45 trang 68 SBT Toán 9 Tập 1: So sánh:

Lời giải:

a) Ta có:

$5\sqrt{2}=\sqrt{5^2\cdot 2}=\sqrt{50};$

$4\sqrt{3}=\sqrt{4^2\cdot 3}=\sqrt{48}.$

Ta thấy 50 > 48 nên $\sqrt{50}>\sqrt{48}$ hay $5\sqrt{2}>4\sqrt{3}.$

b) Ta có:

$\sqrt{36+16}=\sqrt{52};$

$\sqrt{36}+\sqrt{16}=6+4=10=\sqrt{100}.$

Ta thấy 52 < 100 nên $\sqrt{52}<\sqrt{100}$ hay $\sqrt{36+16}<\sqrt{36}+\sqrt{16}.$

c) Ta có:

$\frac{1}{\sqrt{60}}=\frac{1}{\sqrt{4\cdot 15}}=\frac{1}{2\cdot \sqrt{15}}=\frac{1}{2}\cdot \frac{1}{\sqrt{15}};$

$2\sqrt{\frac{1}{15}}=2\cdot \frac{1}{\sqrt{15}}.$

Vì $\frac{1}{2}<2$ và $\frac{1}{\sqrt{15}}>0$ nên $\frac{1}{2}\cdot \frac{1}{\sqrt{15}}<2\cdot \frac{1}{\sqrt{15}}$ hay $\frac{1}{\sqrt{60}}<2\sqrt{\frac{1}{15}}.$

d*) Xét hiệu: ${\left(\sqrt{6}-\sqrt{2}\right)}^2-1=6-2\sqrt{6}\cdot \sqrt{2}+2-1=7-2\sqrt{12}=\sqrt{49}-\sqrt{48}.$

Vì $\sqrt{49}>\sqrt{48}$ nên $\sqrt{49}-\sqrt{48}>0,$ do đó ${\left(\sqrt{6}-\sqrt{2}\right)}^2-1>0,$ hay ${\left(\sqrt{6}-\sqrt{2}\right)}^2>1.$

Mà $\sqrt{6}>\sqrt{2}$ hay $\sqrt{6}-\sqrt{2}>0,$ suy ra $\sqrt{6}-\sqrt{2}>1.$

Bài 46 trang 68 SBT Toán 9 Tập 1: Tốc độ lăn v (m/s) của vật thể có khối lượng m (kg) chịu tác động từ lực E_k (J) được cho bởi công thức $v=\sqrt{\frac{2E_k}{m}}.$

a) Tính tốc độ lăn của quả bóng nặng 3 kg khi một người tác động lực E_k = 18 J lên quả bóng.

b) Muốn lăn một quả bóng 3 kg với tốc độ 6 m/s thì cần tác động lực bao nhiêu jun lên quả bóng đó?

Lời giải:

a) Thay m = 3 (kg) và E_k = 18 (J) vào công thức $v=\sqrt{\frac{2E_k}{m}},$ ta có:

$v=\sqrt{\frac{2\cdot 18}{3}}=\sqrt{12}=\sqrt{2^2\cdot 3}=2\sqrt{3}$ (m/s).

Vậy tốc độ lăn của quả bóng nặng 3 kg khi một người tác động lực E_k = 18 J lên quả bóng là $2\sqrt{3}$ (m/s).

b) Từ $v=\sqrt{\frac{2E_k}{m}}$ ta có: $v^2=\frac{2E_k}{m}$ hay $E_k=\frac{v^2\cdot m}{2}.$

Thay m = 3 (kg) và v = 6 (m/s) vào biểu thức $E_k=\frac{v^2\cdot m}{2},$ ta có:

$E_k=\frac{6^2\cdot 3}{2}=54$ (J).

Vậy muốn lăn một quả bóng 3 kg với tốc độ 6 m/s thì cần tác động lực 54 jun lên quả bóng đó.

Bài 47 trang 68 SBT Toán 9 Tập 1: Rút gọn biểu thức:

Lời giải:

Bài 48 trang 69 SBT Toán 9 Tập 1: Cho biểu thức:

$A=\frac{\sqrt{x}+1}{\sqrt{x}-1}+\frac{\sqrt{x}-1}{\sqrt{x}+1}-\frac{3\sqrt{x}+1}{x-1}$với x ≥ 0, x ≠ 1.

a) Rút gọn biểu thức A.

b) Tính giá trị của biểu thức A tại x = 121.

c) Tìm giá trị của x để $A=\frac{1}{2}.$

d) Tìm giá trị của x để $A=\sqrt{x}-1.$

Lời giải:

a) Với x ≥ 0, x ≠ 1, ta có:

Vậy với x ≥ 0, x ≠ 1 thì $A=\frac{2\sqrt{x}-1}{\sqrt{x}+1}.$

b) Thay x = 121 (thỏa mãn) vào biểu thức $A=\frac{2\sqrt{x}-1}{\sqrt{x}+1},$ ta có:

$A=\frac{2\sqrt{121}-1}{\sqrt{121}+1}=\frac{2\cdot 11-1}{11+1}=\frac{21}{12}.$

Giá trị của biểu thức A tại x = 121 là $\frac{21}{12}$

c) Với x ≥ 0, x ≠ 1, để $A=\frac{1}{2}$ thì $\frac{2\sqrt{x}-1}{\sqrt{x}+1}=\frac{1}{2}$

Suy ra $\frac{2\left(2\sqrt{x}-1\right)}{2\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}+1}{2\left(\sqrt{x}+1\right)}$

x = 1 (không thoả mãn x ≥ 0, x ≠ 1).

Vậy không có giá trị nào của x để $A=\frac{1}{2}.$

d) Với x ≥ 0, x ≠ 1, để $A=\sqrt{x}-1$ thì $\frac{2\sqrt{x}-1}{\sqrt{x}+1}=\sqrt{x}-1.$

Suy ra $2\sqrt{x}-1=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)$

Suy ra $\sqrt{x}=0$ hoặc $\sqrt{x}=2.$

Vì vậy x = 0 (thoả mãn x ≥ 0, x ≠ 1) hoặc x = 4 (thoả mãn x ≥ 0, x ≠ 1).

Vậy x = 0 hoặc x = 4 thì $A=\sqrt{x}-1.$

Bài 49 trang 69 SBT Toán 9 Tập 1: Cho biểu thức:

$B=\frac{x-2}{x+2\sqrt{x}}-\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{x}+2}$ với x > 0.

a) Rút gọn biểu thức B.

b*) Tính giá trị của biểu thức B tại $x=3-2\sqrt{2}.$

c*) Tìm giá trị của x ∈ ℕ để B có giá trị là số nguyên.

Lời giải:

a) Với x > 0, ta có:

Vậy với x > 0 thì $B=\frac{\sqrt{x}-2}{\sqrt{x}}.$

b*) Ta có: $x=3-2\sqrt{2}=2-2\sqrt{2}+1={\left(\sqrt{2}-1\right)}^2>0$ thỏa mãn điều kiện.

Suy ra $\sqrt{x}=\sqrt{{\left(\sqrt{2}-1\right)}^2}=\left|\sqrt{2}-1\right|=\sqrt{2}-1.$

Thay $\sqrt{x}=3-2\sqrt{2}$ vào biểu thức $B=\frac{\sqrt{x}-2}{\sqrt{x}},$ ta có:

$\frac{\left(\sqrt{2}-1\right)-2}{\sqrt{2}-1}=\frac{\left(\sqrt{2}-3\right)\left(\sqrt{2}+1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}=\frac{2+\sqrt{2}-3\sqrt{2}-3}{2-1}=-1-2\sqrt{2}.$

Vậy giá trị của biểu thức B tại $x=3-2\sqrt{2}$ là $-1-2\sqrt{2}.$

c*) Với x > 0, ta có: $B=\frac{\sqrt{x}-2}{\sqrt{x}}=1-\frac{2}{\sqrt{x}}.$

Với x ∈ ℕ^* thì B có giá trị là số nguyên khi $2⋮\sqrt{x}$ hay $\sqrt{x}$ ∈ Ư(2) = {1; –1; 2; –2}.

Mà $\sqrt{x}>0$ với x > 0, suy ra $\sqrt{x}=1$ hoặc $\sqrt{x}=2.$

Do đó x = 1 hoặc x = 4 (đều thoả mãn x > 0).

Vậy x ∈ {1; 4} thì B có giá trị là số nguyên.

Bài 50 trang 69 SBT Toán 9 Tập 1: Cho biểu thức:

$C=\left(\frac{\sqrt{x}-2}{x-1}-\frac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right)\cdot \frac{{\left(1-x\right)}^2}{2}$ với x ≥ 0, x ≠ 1.

a) Rút gọn biểu thức C.

b*) Tìm giá trị lớn nhất của C.

c*) Tìm giá trị của x để C có giá trị là số dương.

Lời giải:

a) Với x ≥ 0, x ≠ 1, ta có:

Vậy với x ≥ 0, x ≠ 1 thì $C=\sqrt{x}-x.$

b*) Với x ≥ 0, x ≠ 1, ta có:

$C=\sqrt{x}-x=\frac{1}{4}-\left(x-\sqrt{x}+\frac{1}{4}\right)=\frac{1}{4}-{\left(\sqrt{x}-\frac{1}{2}\right)}^2.$

Với x ≥ 0, x ≠ 1, ta có: ${\left(\sqrt{x}-\frac{1}{2}\right)}^2\ge 0$ hay $\frac{1}{4}-{\left(\sqrt{x}-\frac{1}{2}\right)}^2\le \frac{1}{4}.$

Vậy giá trị lớn nhất của C là $\frac{1}{4}$ khi $\sqrt{x}-\frac{1}{2}=0$ hay $\sqrt{x}=\frac{1}{2}$ nên $x=\frac{1}{4}$ (thoả mãn x ≥ 0, x ≠ 1).

c*) Với x ≥ 0, x ≠ 1, ta có: $C=\sqrt{x}-x=\sqrt{x}\left(1-\sqrt{x}\right).$

Do $\sqrt{x}\ge 0$ với x ≥ 0 nên C > 0 khi $\sqrt{x}>0$ và $1-\sqrt{x}>0$ hay x > 0 và $\sqrt{x}<1.$

Suy ra x > 0 và x < 1.

Vậy 0 < x < 1 thì C có giá trị là số dương.

Bài 51 trang 69 SBT Toán 9 Tập 1: Tìm x, biết:

Lời giải:

a) Với x ≥ 0, ta có:

15x = 6²

15x = 36

$x=\frac{12}{5}$ (thỏa mãn x ≥ 0).

Vậy $x=\frac{12}{5}.$

b) $\sqrt{9x^2}=\left|-18\right|$

$\sqrt{{\left(3x\right)}^2}=18$

|3x| = 18

Suy ra 3x = 18 hoặc 3x = ‒18

x = 6 hoặc x = ‒6.

Vậy x = 6 hoặc x = ‒6.

c) x² – 8 = 0

x² = 8

$x^2={\left(2\sqrt{2}\right)}^2={\left(-2\sqrt{2}\right)}^2$

Suy ra $x=2\sqrt{2}$ hoặc $x=-2\sqrt{2}.$

Vậy $x=2\sqrt{2}$ hoặc $x=-2\sqrt{2}.$

d) Với x ≥ 7, ta có:

$\sqrt{x^2-49}-\sqrt{x-7}=0$

$\sqrt{\left(x-7\right)\left(x+7\right)}-\sqrt{x-7}=0$

$\sqrt{x-7}\cdot \sqrt{x+7}-\sqrt{x-7}=0$ (vì x ≥ 7 nên x – 7 ≥ 0 và x + 7 > 0)

$\sqrt{x-7}\left(\sqrt{x+7}-1\right)=0$

Suy ra $\sqrt{x-7}=0$ hoặc $\sqrt{x+7}-1=0.$

⦁ Giải phương trình $\sqrt{x-7}=0.$

$\sqrt{x-7}=0$
x – 7 = 0

x = 7 (thỏa mãn x ≥ 7).

⦁ Giải phương trình $\sqrt{x+7}-1=0.$

$\sqrt{x+7}-1=0$

$\sqrt{x+7}=1$

x + 7 = 1

x = ‒6 (không thoả mãn x ≥ 7).

Vậy x = 7.

Xem thêm Lời giải bài tập Toán 9 sách Cánh diều hay, chi tiết khác:

Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài 1: Tỉ số lượng giác của góc nhọn

Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 3: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài tập cuối chương 4