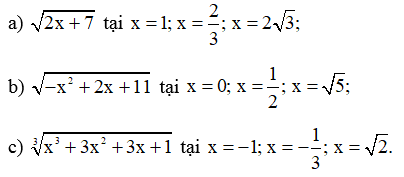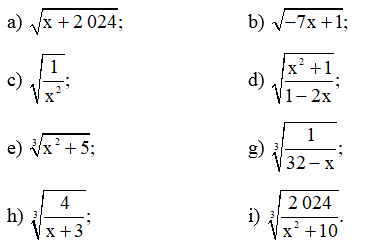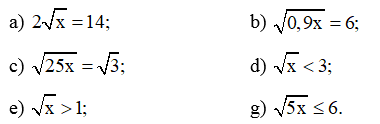Sách bài tập Toán 9 Bài 3 (Cánh diều): Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

Giải SBT Toán 9 Bài 3: Căn thức bậc hai và căn thức bậc ba của biểu thức đại số - Cánh diều

Bài 24 trang 61 SBT Toán 9 Tập 1: Tính giá trị của mỗi biểu thức sau:

Lời giải:

a) Xét biểu thức $\sqrt{2x+7}.$

Thay x = 1 vào biểu thức trên, ta được:

$\sqrt{2\cdot 1+7}=\sqrt{2+7}=\sqrt{9}=3.$

Thay $x=\frac{2}{3}$ vào biểu thức trên, ta được:

$\sqrt{2\cdot \frac{2}{3}+7}=\sqrt{\frac{4}{3}+7}=\sqrt{\frac{25}{3}}=\frac{\sqrt{25}}{\sqrt{3}}=\frac{5}{\sqrt{3}}=\frac{5\sqrt{3}}{{\left(\sqrt{3}\right)}^2}=\frac{5\sqrt{3}}{3}.$

Thay $x=2\sqrt{3}$ vào biểu thức trên, ta được:

$\sqrt{2\cdot 2\sqrt{3}+7}=\sqrt{4\sqrt{3}+7}=\sqrt{2^2+2\cdot 2\cdot \sqrt{3}+{\left(\sqrt{3}\right)}^2}=\sqrt{{\left(2+\sqrt{3}\right)}^2}=2+\sqrt{3}.$

b) Xét biểu thức $\sqrt{-x^2+2x+11}$

Thay x = 0 vào biểu thức trên, ta được:

$\sqrt{-0^2+2\cdot 0+11}=\sqrt{11}.$

Thay $x=\frac{1}{2}$ vào biểu thức trên, ta được:

$\sqrt{-{\left(\frac{1}{2}\right)}^2+2\cdot \frac{1}{2}+11}=\sqrt{-\frac{1}{4}+1+11}=\sqrt{\frac{47}{4}}=\frac{\sqrt{47}}{\sqrt{4}}=\frac{\sqrt{47}}{2}.$

Thay $x=\sqrt{5}$ vào biểu thức trên, ta được:

$\sqrt{-{\left(\sqrt{5}\right)}^2+2\cdot \sqrt{5}+11}=\sqrt{-5+2\sqrt{5}+11}=\sqrt{6+2\sqrt{5}}$

$=\sqrt{{\left(\sqrt{5}\right)}^2+2\cdot \sqrt{5}\cdot 1+1^2}=\sqrt{{\left(\sqrt{5}+1\right)}^2}=\sqrt{5}+1.$

c) Xét biểu thức $\sqrt[3]{x^3+3x^2+3x+1}=\sqrt[3]{{\left(x+1\right)}^3}=x+1.$

Thay x = ‒1 vào biểu thức trên, ta được: ‒1 + 1 = 0.

Thay $x=-\frac{1}{3}$ vào biểu thức trên, ta được: $-\frac{1}{3}+1=\frac{2}{3}.$

Thay $x=\sqrt{2}$ vào biểu thức trên, ta được: $\sqrt{2}+1.$

Bài 25 trang 61 SBT Toán 9 Tập 1: Tìm điều kiện xác định cho mỗi biểu thức sau:

Lời giải:

a) Biểu thức $\sqrt{x+2024}$ xác định khi x + 2 024 ≥ 0 hay x ≥ ‒2 024.

b) Biểu thức $\sqrt{-7x+1}$ xác định khi ‒7x + 1 ≥ 0 hay ‒7x ≥ ‒1, do đó $x\le \frac{1}{7}.$

c) Biểu thức $\sqrt{\frac{1}{x^2}}$ xác định khi $\frac{1}{x^2}\ge 0$ và x ≠ 0.

Xét $\frac{1}{x^2}\ge 0,$ ta có x² > 0. Điều này xảy ra khi và chỉ khi x ≠ 0.

Vậy $\sqrt{\frac{1}{x^2}}$ xác định khi x ≠ 0.

d) Biểu thức $\sqrt{\frac{x^2+1}{1-2x}}$ xác định khi $\frac{x^2+1}{1-2x}\ge 0$ và 1 – 2x ≠ 0.

⦁ Xét $\frac{x^2+1}{1-2x}\ge 0,$ ta có 1 – 2x > 0 (do x² + 1 ≥ 0 với mọi x), hay –2x > –1 nên $x<\frac{1}{2}.$

⦁ Xét 1 – 2x ≠ 0, ta có 2x ≠ 1 hay $x\ne \frac{1}{2}.$

Kết hợp các điều kiện, ta có biểu thức $\sqrt{\frac{x^2+1}{1-2x}}$ xác định khi $x<\frac{1}{2}.$

e) Biểu thức $\sqrt[3]{x^2+5}$ xác định với mọi số thực x vì x² + 5 xác định với mọi số thực x.

g) Biểu thức $\sqrt[3]{\frac{1}{32-x}}$ xác định khi $\frac{1}{32-x}$ xác định, hay 32 ‒ x ≠ 0 nên x ≠ 32.

h) Biểu thức $\sqrt[3]{\frac{4}{x+3}}$ xác định khi $\frac{4}{x+3}$ xác định, hay x + 3 ≠ 0 nên x ≠ ‒3.

i) Biểu thức $\sqrt[3]{\frac{2024}{x^2+10}}$ xác định khi $\frac{2024}{x^2+10}$ xác định.

Với mọi số thực x ta có x² + 10 ≥ 10 nên x² + 10 ≠ 0 với mọi số thực x.

Do đó $\frac{2024}{x^2+10}$ xác định với mọi số thực x.

Vậy biểu thức $\sqrt[3]{\frac{2024}{x^2+10}}$ xác định với mọi số thực x.

Bài 26 trang 61 SBT Toán 9 Tập 1: Điện áp U (V) yêu cầu cho một mạch điện được cho bởi công thức $U=\sqrt{P\cdot R},$ trong đó P (W) là công suất tiêu thụ của điện trở và R (Ω) là giá trị điện trở.

a) Tính điện áp để thắp sáng cho bóng đèn A có công suất tiêu thụ là 100 W và giá trị điện trở là 110 Ω (làm tròn kết quả đến hàng đơn vị của vôn).

b) Bóng đèn B có điện áp 110 V và giá trị điện trở là 88 Ω. Công suất tiêu thụ của bóng đèn B có lớn hơn công suất tiêu thụ của bóng đèn A hay không? Vì sao?

Lời giải:

a) Bóng đèn A có công suất tiêu thụ là 100 W nên P = 100 (W).

Bóng đèn A có giá trị điện trở là 110 Ω nên R = 110 (Ω).

Thay vào công thức $U=\sqrt{P\cdot R},$ ta có:

$U=\sqrt{100\cdot 110}=10\sqrt{110}\approx 105$ (V).

Vậy điện áp để thắp sáng cho bóng đèn A có công suất tiêu thụ là 100 W và giá trị điện trở là 110 Ω khoảng 105 V.

b) Bóng đèn B có điện áp là 110 V nên U = 110 (V).

Bóng đèn B có giá trị điện trở là 88 Ω nên R = 88 (Ω).

Thay U = 110 (V) và R = 88 (Ω) vào $U=\sqrt{P\cdot R},$ ta có:

$110=\sqrt{P\cdot 88}$

Suy ra 88P = 12 100, do đó P = 137,5 (W).

Do 137,5 > 100 nên công suất tiêu thụ của bóng đèn B lớn hơn công suất tiêu thụ của bóng đèn A.

Bài 27 trang 61 SBT Toán 9 Tập 1: Tốc độ v (m/s) của một chiếc ca nô được tính theo độ dài đường sóng nước sau đuôi l (m) của ca nô bởi công thức $v=5\sqrt{l}.$

a) Một ca nô để lại đường sóng nước sau đuôi dài 4 m thì tốc độ của nó là bao nhiêu kilômét trên giờ?

b) Khi ca nô di chuyển với tốc độ 54 km/h thì đường sóng nước sau đuôi dài bao nhiêu mét?

Lời giải:

a) Một ca nô để lại đường sóng nước sau đuôi dài 4 m nên l = 4 (m).

Thay l = 4 (m) vào công thức $v=5\sqrt{l},$ ta có:

$v=5\sqrt{4}=5\cdot 2=10$ (m/s) = 36 (km/h).

Vậy ca nô để lại đường sóng nước sau đuôi dài 4 m thì tốc độ của nó là 36 kilômét trên giờ.

b) Đổi 54 km/h = 15 m/s.

Ca nô di chuyển với tốc độ 15 m/s nên v = 15 (m/s).

Thay v = 15 (m/s) vào công thức $v=5\sqrt{l},$ ta có:

$15=5\sqrt{l}$ nên $\sqrt{l}=3,$ do đó l = 9 (m).

Vậy khi ca nô di chuyển với tốc độ 54 km/h thì đường sóng nước sau đuôi dài 9 mét.

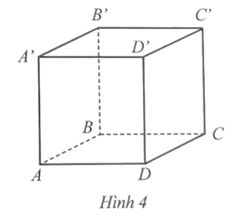
Bài 28 trang 61 SBT Toán 9 Tập 1: Một chất điểm di chuyển từ đỉnh A’ đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). Quãng đường ngắn nhất mà chất điểm đó di chuyển là bao nhiêu decimét?

Lời giải:

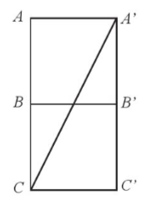
Giả sử chất điểm đó di chuyển qua các mặt ABB’A’ và BCC’B’ của hình lập phương (các trường hợp khác tương tự).

Hình vẽ trên là hình khai triển của các mặt ABB’A’ và BCC’B’.

Do tam giác AA’C vuông tại A nên theo định lí Pythagore, ta có:

A’C² = AA’ + AC²

Suy ra A’C² = AA’² + (AB + BC)² = 1² + (1 + 1)² = 5.

Do đó $A^{\text{'}}C=\sqrt{5}\left(dm\right).$

Vậy quãng đường ngắn nhất mà chất điểm đó di chuyển là $\sqrt{5}$ dm.

Bài 29 trang 61 SBT Toán 9 Tập 1: a) Tìm giá trị nhỏ nhất của biểu thức: $A=5+\sqrt{2x-1}.$

b) Tìm giá trị lớn nhất của biểu thức: $B=2024-\sqrt{5x+2}.$

Lời giải:

a) Điều kiện xác định của biểu thức A là: 2x ‒ 1 ≥ 0 hay $x\ge \frac{1}{2}.$

Khi đó, ta có $\sqrt{2x-1}\ge 0$ nên $5+\sqrt{2x-1}\ge 5$ hay A ≥ 5.

Vậy giá trị nhỏ nhất của biểu thức A là 5 khi 2x ‒ 1 = 0 hay $x=\frac{1}{2}.$

b) Điều kiện xác định biểu thức B là: 5x + 2 ≥ 0 hay $x\ge -\frac{2}{5}.$

Khi đó, ta có $\sqrt{5x+2}\ge 0$ nên $-\sqrt{5x+2}\le 0.$

Suy ra $2024-\sqrt{5x+2}\le 2024$ hay B ≤ 2 024.

Vậy giá trị lớn nhất của biểu thức B là 2 024 khi 5x + 2 = 0 hay $x=-\frac{2}{5}.$

Bài 30 trang 62 SBT Toán 9 Tập 1: Tìm x không âm, biết:

Lời giải:

Với x ≥ 0, ta có:

a) $2\sqrt{x}=14$

$\sqrt{x}=7$

x = 7²

x = 49 (thỏa mãn).

Vậy x = 49.

b) $\sqrt{0,9x}=6$

0,9x = 6²

0,9x = 36

x = 40 (thỏa mãn).

Vậy x = 40.

c) $\sqrt{25x}=\sqrt{3}$

25x = 3

x = 0,12 (thỏa mãn).

Vậy x = 0,12.

d) $\sqrt{x}<3$

0 ≤ x < 3²

0 ≤ x < 9.

Vậy 0 ≤ x < 9.

e) $\sqrt{x}>1$

x > 1² > 0

x > 1.

Kết hợp điều kiện x ≥ 0, ta có: x > 1.

g) $\sqrt{5x}\le 6$

0 ≤ 5x ≤ 6²

0 ≤ 5x ≤ 36

0 ≤ x ≤ 7,2.

Xem thêm Lời giải bài tập Toán 9 sách Cánh diều hay, chi tiết khác:

Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài tập cuối chương 3

Bài 1: Tỉ số lượng giác của góc nhọn

Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông

Bài 3: Một số hệ thức về cạnh và góc trong tam giác vuông