Lý thuyết Hình tam giác. Diện tích hình tam giác (mới 2022 + Bài Tập) - Toán lớp 5

Lý thuyết Hình tam giác - Diện tích hình tam giác lớp 5

1. Hình tam giác

a) Cấu trúc

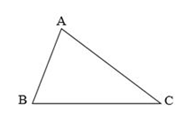
Hình tam giác ABC có:

- Ba cạnh là: cạnh AB, cạnh AC, cạnh BC.

- Ba đình là: đinh A, đnh B, đinh C.

- Ba góc là:

Góc đnh A, cạnh AB và AC (gọi tắt là góc A);

Góc đnh B, cạnh BA và BC (gọi tắt là góc B);

Góc đnh C, cạnh CA và CB(gọi tắt là góc C).

b) Các loại hình tam giác

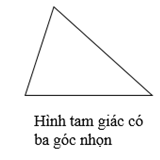
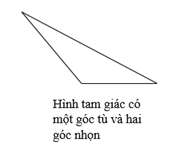
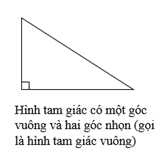
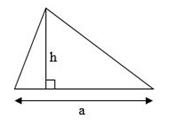
c) Cách xác định đáy và đường cao của hình tam giác

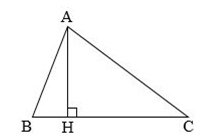
BC là đáy, AH là đường cao tương ứng với đáy BC. Độ dài AH là chiều cao

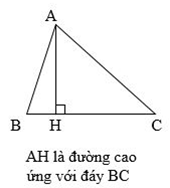
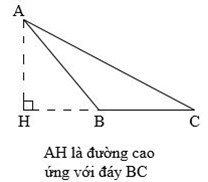
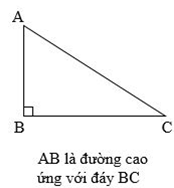
Chú ý: Trong hình tam giác, độ dài đoạn thẳng từ đỉnh vuông góc với đáy tương ứng gọi là chiều cao của hình tam giác

2. Diện tích hình tam giác

Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2

$S=\frac{a\times h}{2} hoặc S = a\times h:2$

(S là diện tích, a là độ dài đáy, h là chiều cao)

Chú ý: Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho 2.

Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là 13cm và chiều cao là 8cm.

Phương pháp giải: Độ dài đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2.

Cách giải:

Diện tích hình tam giác đó là:

13 x 8 : 2 = 52 (cm²)

Đáp số: 52cm²

Ví dụ 2: Tính diện tích hình tam giác có độ dài đáy là 2m và chiều cao là 15dm.

Phương pháp giải: Độ dài đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, 2m = 20dm, sau đó tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2

Bài giải

Đổi: 2m = 20dm

Diện tích hình tam giác đó là:

20 x 15 : 2 = 150 dm²

Đáp số: 150 dm²

3. Một số dạng bài tập

Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao

Phương pháp: Áp dụng công thức: $S=\frac{a\times h}{2} hoặc S = a\times h:2$

(S là diện tích, a là độ dài đáy, h là chiều cao)

Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao

Phương pháp: Từ công thức tính diện tích $S=\frac{a\times h}{2} hoặc S = a\times h:2$, ta có công thức tính độ dài đáy như sau: $a=\frac{S\times 2}{h} hoặc a=S\times 2:h$

Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy

Phương pháp: Từ công thức tính diện tích $S=\frac{a\times h}{2} hoặc S = a\times h:2$, ta có công thức tính chiều cao như sau: $h=\frac{S\times 2}{a}hoặc h=S\times 2:a$

Dạng 4: Toán có lời văn

Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.

Xem thêm các bài tổng hợp lý thuyết Toán lớp 5 đầy đủ, chi tiết khác:

Lý thuyết Hình thang. Diện tích hình thang

Lý thuyết Hình tròn. Đường tròn. Chu vi hình tròn

Lý thuyết Diện tích hình tròn

Lý thuyết Hình hộp chữ nhật. Hình lập phương

Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật