Lý thuyết Tổng hợp kiến thức cơ bản (mới 2022 + Bài Tập) - Toán lớp 5

Lý thuyết Tổng hợp kiến thức cơ bản Toán lớp 5

ÔN TẬP VÀ BỔ SUNG VỀ PHÂN SỐ

1. Các tính chất cơ bản của phân số

*) Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác  thì được một phân số bằng phân số đã cho.

Ví dụ: $\frac{5}{6}=\frac{5\times 3}{6\times 3}=\frac{15}{16}$

*) Nếu chia cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác  thì được một phân số bằng phân số đã cho.

Ví dụ: $\frac{15}{18}=\frac{15:3}{18:3}=\frac{5}{6}$

2. Rút gọn phân số

Phương pháp:

+ Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1. 

+ Chia tử số và mẫu số cho số đó.

+ Cứ làm như thế cho đến khi nhận được phân số tối giản.  

Ví dụ: Rút gọn phân số $\frac{12}{16}$

$\frac{12}{16}=\frac{12:2}{16:2}=\frac{6}{8}=\frac{6:2}{8:2}=\frac{3}{4}$ hay $\frac{12}{16}=\frac{12:4}{16:4}=\frac{3}{4}$

3. Quy đồng mẫu số của các phân số

Phương pháp:

+ Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

+ Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

Ví dụ: Quy đồng mẫu hai phân số $\frac{5}{6}$ và $\frac{3}{5}$

$\begin{array}{l}\frac{5}{6}=\frac{5\times 5}{6\times 5}=\frac{25}{30}\\ \frac{3}{5}=\frac{3\times 6}{6\times 6}=\frac{18}{36}\end{array}$

4. So sánh hai phân số

4.1. So sánh hai phân số cùng mẫu số

Trong hai phân số cùng mẫu số:

• Phân số nào có tử số bé hơn thì bé hơn.
• Phân số nào có tử số lớn hơn thì lớn hơn.
• Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

Ví dụ: So sánh phân số $\frac{6}{7}$ và $\frac{9}{7}$

Vì $6<9$ nên $\frac{6}{7}<\frac{9}{7}$.

4.2. So sánh hai phân số không cùng mẫu số

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

Ví dụ: So sánh hai phân số $\frac{2}{3}$ và $\frac{3}{4}$

Quy đồng mẫu số hai phân số $\frac{2}{3}$ và $\frac{3}{4}$, ta có:

$\begin{array}{l}\frac{2}{3}=\frac{2\times 4}{3\times 4}=\frac{8}{12}\\ \frac{3}{4}=\frac{3\times 3}{4\times 3}=\frac{9}{12}\end{array}$

Vì $8<9$ nên $\frac{8}{12}<\frac{9}{12}$.

Vậy $\frac{2}{3}<\frac{3}{4}$.

5. Phân số thập phân

Khái niệm: Các phân số có mẫu số là 10, 100, 1000,... được gọi là phân số thập phân

Ví dụ: $\frac{3}{10},\frac{7}{100},\frac{11}{1000},\mathrm{...}$

6. Phép cộng và trừ hai phân số có cùng mẫu số

Phương pháp: Muốn cộng (hoặc trừ) hai phân số cùng mẫu số ta cộng (hoặc trừ) hai tử số với nhau và giữ nguyên mẫu số.

Ví dụ. Tính:

1) $\frac{3}{7}+\frac{2}{7}$

2) $\frac{3}{7}-\frac{2}{7}$

Bài giải

1) $\frac{3}{7}+\frac{2}{7}=\frac{3+2}{7}=\frac{5}{7}$

2) $\frac{3}{7}-\frac{2}{7}=\frac{3-2}{7}=\frac{1}{7}$

7. Phép cộng và trừ hai phân số không cùng mẫu số

Phương pháp: Muốn cộng (hoặc trừ) hai phân số khác mẫu số ta quy đồng mẫu số, rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.
Ví dụ. Tính:

1) $\frac{8}{9}+\frac{7}{5}$

2) $\frac{7}{5}-\frac{8}{9}$

Bài giải

1) $\frac{8}{9}+\frac{7}{5}=\frac{40}{45}+\frac{63}{45}$

$=\frac{40+63}{45}=\frac{103}{45}$

2) $\frac{7}{5}-\frac{8}{9}=\frac{63}{45}-\frac{40}{45}$

$=\frac{63-40}{45}=\frac{23}{45}$

8.  Phép nhân và phép chia hai phân số

Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

Ví dụ: $\frac{2}{3}\times \frac{4}{9}=\frac{2\times 4}{3\times 9}=\frac{8}{27}$

Muốn chia hai phân số cho một phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

Ví dụ: 

$$\begin{gathered} \frac{2}{3}:\frac{9}{4}=\frac{2}{3}\times \frac{4}{9} \\ =\frac{2\times 4}{3\times 9}=\frac{8}{27} \end{gathered}$$

HỖN SỐ

1.  Khái niệm hỗn số

Hỗn số gồm hai thành phần là phân nguyên và phần phân số.

Ví dụ: Hỗn số $2\frac{1}{4}$ được đọc là “hai và một phần bốn” có phần nguyên là 2 và phần phân số là $\frac{1}{4}$

Chú ý: Phần phân số của hỗn số bao giờ cũng nhỏ hơn 1

2. Cách chuyển hỗn số thành phân số

Phương pháp:

+ Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

+ Mẫu số bằng mẫu số ở phần phân số.

Ví dụ: Chuyển các hỗn số thành phân số $3\frac{1}{4};5\frac{2}{3};7\frac{3}{7}$

Bài giải

$3\frac{1}{4}=\frac{3\times 4+1}{4}=\frac{13}{4}$

$\begin{array}{l}5\frac{2}{3}=\frac{5\times 3+2}{3}=\frac{17}{3}\\ 7\frac{3}{7}=\frac{7\times 7+3}{7}=\frac{52}{3}\end{array}$

3. Cách chuyển phân số thành hỗn số

Phương pháp:

+ Tính phép chia tử số cho mẫu số

+ Giữ nguyên mẫu số của phần phân số; Tử số bằng số dư của phép chia tử số cho mẫu số

+ Phần nguyên bằng thương của phép chia tử số cho mẫu số

Ví dụ. Viết phân số $\frac{14}{3}$ thành hỗn số

Thực hiện phép chia:

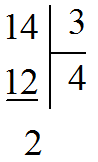
Vậy $\frac{14}{3}=4\frac{2}{3}$

4. Các phép toán với hỗn số

4.1. Phép cộng, trừ hỗn số

Cách 1. Chuyển hỗn số về phân số

Ví dụ.

a) $3\frac{1}{2}+4\frac{1}{3}=\frac{7}{2}+\frac{13}{3}$

$=\frac{21}{6}+\frac{26}{6}=\frac{47}{6}$

b) $2\frac{2}{3}-1\frac{4}{7}=\frac{8}{3}-\frac{11}{7}$

$=\frac{56}{21}-\frac{33}{21}=\frac{23}{21}$

Cách 2. Tách hỗn số thành phần nguyên và phần phân số

Ví dụ.

a) $3\frac{1}{2}+4\frac{1}{3}$

$$\begin{gathered} =\left(3+4\right)+\left(\frac{1}{2}+\frac{1}{3}\right) \\ =7+\frac{5}{6}=\frac{47}{6} \end{gathered}$$

b) $2\frac{2}{3}-1\frac{4}{7}$

$$\begin{gathered} =\left(2-1\right)+\left(\frac{2}{3}-\frac{4}{7}\right) \\ =1+\frac{2}{21}=\frac{23}{21} \end{gathered}$$

4.2. Phép nhân, chia hỗn số

Phương pháp: Muốn nhân (hoặc chia) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi nhân (hoặc chia) hai phân số vừa chuyển đổi.

Ví dụ.

a) $2\frac{2}{3}\times 5\frac{1}{4}$

$=\frac{8}{3}\times \frac{21}{4}=14$

b) $3\frac{1}{2}:2\frac{1}{4}$

$$\begin{gathered} =\frac{7}{2}:\frac{9}{4} \\ =\frac{7}{2}\times \frac{4}{9}=\frac{14}{9} \end{gathered}$$

5. So sánh hỗn số

Cách 1. Chuyển hỗn số về phân số

Ví dụ. So sánh hai hỗn số $2\frac{3}{5}$ và $2\frac{2}{3}$

$\begin{array}{l}2\frac{3}{5}=\frac{2\times 5+3}{5}=\frac{13}{5}\\ 2\frac{2}{3}=\frac{2\times 3+2}{3}=\frac{8}{3}\end{array}$

Quy đồng:

$\begin{array}{l}\frac{13}{5}=\frac{13\times 3}{5\times 3}=\frac{39}{15}\\ \frac{8}{3}=\frac{8\times 5}{3\times 5}=\frac{40}{15}\end{array}$

Vì $\frac{39}{15}<\frac{40}{15}$ nên $\frac{13}{5}<\frac{8}{3}$.

Vậy $2\frac{3}{5}<2\frac{2}{3}$.

Cách 2. So sánh phần nguyên và phần phân số

Ví dụ. So sánh hai hỗn số $5\frac{3}{8}$ và $6\frac{1}{2}$

Hỗn số $5\frac{3}{8}$ có phần nguyên là 5.

Hỗn số $6\frac{1}{2}$ có phần nguyên là 6.

Vì $6>3$ nên $6\frac{1}{2}>5\frac{3}{8}$.

Vậy $6\frac{1}{2}>5\frac{3}{8}$.

SỐ THẬP PHÂN VÀ CÁC PHÉP TÍNH VỚI SỐ THẬP PHÂN

1. Khái niệm số thập phân

Ôn lại phân số thập phân: Các phân số có mẫu số là 10, 100, 1000,… được gọi là phân số thập phân.

Ví dụ: $\frac{1}{10};\frac{3}{100};\dots$

Mỗi số thập phân gồm hai phần: Phần nguyên và phần thập phân (chúng được phân cách bởi dấu phẩy)

Ví dụ. Số thập phân 4,35 gồm hai phần: Phần nguyên (4) và phần thập phân (35)

2. Chuyển các phân số thành số thập phân

Phương pháp: Nếu phân số đã cho chưa là phân số thập phân thì ta chuyển các phân số thành phân số thập phân rồi chuyển thành số thập phân.

Ví dụ. Chuyển các phân số sau thành phân số thập phân:

a) $\frac{3}{100}$

b) $\frac{3}{2}$

Bài giải

a) $\frac{3}{100}=0,03$

b) $\frac{3}{2}=\frac{15}{10}=1,5$

3. Chuyển số thập phân thành phân số

Phương pháp: Viết số thập phân dưới dạng phân số thập phân sau đó thực hiện các bước rút gọn phân số thập phân đó.

(1, 2, 3 chữ số phần thập phân khi chuyển sang phân số thập phân có mẫu số là 10, 100, 100,…)

Ví dụ.

$0,1=\frac{1}{10} 0,12=\frac{12}{100}=\frac{3}{25}$

4. Viết các số đo độ dài, khối lượng… dưới dạng số thập phân

Phương pháp:

- Tìm mối liên hệ giữa hai đơn vị đo đã cho.

- Chuyển số đo độ dài đã cho thành phân số thập phân có đơn vị đo lớn hơn.

- Chuyển từ số đo độ dài dưới dạng phân số thập phân thành số đo độ dài tương ứng dưới dạng số thập phân có đơn vị lớn hơn.

Ví dụ. Viết số đo dưới dạng phân số thập phân và số thập phân

a) $2cm=\frac{2}{10}dm=0,2dm$

b) $7cm=\frac{7}{100}m=0,07m$

5. Viết hỗn số thành phân số thập phân

Phương pháp: Đổi hỗn số về dạng phân số thập phân, sau đó chuyển thành số thập phân

Ví dụ. Viết hỗn số thành số thập phân:

a) $3\frac{5}{10}=\frac{35}{10}=3,5$

b) $5\frac{7}{25}=5\frac{28}{100}=\frac{528}{100}=5,28$

6. Phép cộng và phép trừ các số thập phân

6.1. Phép cộng hai số thập phân

Muốn cộng hai số thập phân ta làm như sau:

- Viết số hạng này dưới số hạng kia làm sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau.

- Cộng như cộng các số tự nhiên.

- Viết dấu phẩy ở tổng thẳng cột với các dấu phẩy của các số hạng.

Ví dụ. Tính:

a) 1,87 + 2,24

b) 15,9 + 8,75

Bài giải

a) $\frac{+\begin{array}{c}1,87\\ 2,24\end{array}}{4,11}$

Vậy 1,87 + 2,24 = 4,11

b) $\frac{+\begin{array}{c}15,9\\ 8,75\end{array}}{24,65}$

Vậy 15,9 + 8,75 = 24,65

6.2. Phép trừ hai số thập phân

Muốn trừ một số thập phân cho một số thập phân ta làm như sau:

- Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột nhau.

- Thực hiện phép trừ như trừ các số tự nhiên.

- Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ.

Ví dụ. Tính:

a) 4,29 - 1,84

b) 45,8 - 19,26

Bài giải

a) $\frac{-\begin{array}{c}4,29\\ 1,84\end{array}}{2,45}$

Vậy 4,29 - 1,84 = 2,45

b) $\frac{-\begin{array}{c}45,8\\ 19,26\end{array}}{26,54}$

Vậy 45,8 - 19,26 = 26,54

6.3. Phép nhân các số thập phân

a) Nhân một số thập phân với một số tự nhiên

Muốn nhân một số thập phân với một số tự nhiên ta là như sau:

+ Nhân như nhân các số tự nhiên

+ Đếm xem trong phần thập phân của số thập phân có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.

Ví dụ. Đặt tính và tính: 1,46x12

$\begin{array}{l}\times \begin{array}{c}1,46\\ \underset{¯}{12}\end{array}\\ \begin{array}{c}292\\ \underset{¯}{146}\end{array}\\ 17,52\end{array}$

b) Nhân một số thập phân với 10, 100, 1000,…

Muốn nhân một số thập phân với 10, 100, 100,… ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba,… chữ số.

Ví dụ: $3,2\times 10=32; 3,456\times 100=345,6$

c) Nhân một số thập phân với một số thập phân

Muốn nhân một số thập phân với một số thập phân ta làm như sau:

+ Thực hiện phép nhân như nhân các số tự nhiên

+ Đếm xem trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái

Ví dụ. Đặt tính và tính: 4,75x1,3

Bài giải

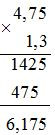
Vậy $4,75\times 1,3=6,175$.

(hai thừa số có tất cả ba chữ số ở phần thập phân, ta dùng dấu phẩy tách ở tích ra ba chữ số kể từ trái sang phải)

d) Nhân một số thập phân với 0,1; 0,01; 0,001;…

Muốn nhân một số thập phân với 0,1; 0,01; 0,001;… ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba,… chữ số.

Ví dụ: 

$$\begin{gathered} 579,8\times 0,1 \\ =57,98; 805,13\times 0,01 \\ =8,0513 \end{gathered}$$

6.4. Tính chất của phép nhân

a) Tính chất giao hoán: $a\times b=b\times a$

b) Nhân với 0 và 1: $a\times 0=0\times a=0;$$a\times 1=1\times a=a$

b) Tính chất kết hợp: $\left(a\times b\right)\times c=a\times \left(b\times c\right)$

c) Tính chất phân phối của phép nhân và phép cộng: $\left(a+b\right)\times c=a\times c+b\times c$

6.5. Phép chia các số thập phân

a) Chia một số thập phân cho một số tự nhiên

Muốn chia một số thập phân cho một số tự nhiên ta làm như sau:

- Chia phần nguyên của số bị chia cho số chia.

- Viết dấu phẩy vào bên phải thương đã tìm được trước khi lấy chữ số đầu tiên ở phần thập phân của số bị chia đẻ thực hiện phép chia.

- Tiếp tục chia với từng chữ số thập phân của số bị chia.

Ví dụ. Đặt tính rồi tính

a) 5,28:4

b) 0,36:9

Bài giải

a)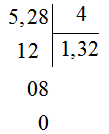 

Vậy 5,28:4=1,32

b)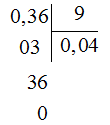 

Vậy 0,36:9= 0,04

b) Chia một số thập phân cho 10, 100, 1000,…

Muốn chia một số thập phân cho 10, 100, 1000,… ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba,… chữ số.

Ví dụ: 

$\begin{array}{l}89,13:100=0,8913\\ 213,8:10=21,38\end{array}$

c) Chia một số tự nhiên cho một số tự nhiên mà thương tìm được là một số thập phân

Khi chia một số tự nhiên cho một số tự nhiên mà còn dư, ta tiếp tục chia như sau:

+ Viết dấu phẩy vào bên phải số thương.

+ Biết thêm vào bên phải số dư một chữ số 0 rồi chia tiếp.

+ Nếu còn dư nữa, ta lại viết thêm vào bên phải số dư mới một chữ số 0 rồi tiếp tục chia, và có thể cứ làm như thế mãi.

Ví dụ. Đặt tính rồi tính:

a) 12:5

b) 43:52

Bài giải

a)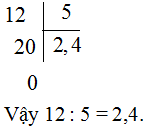

b)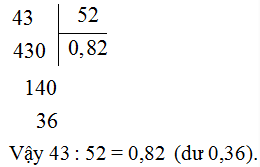

d) Chia một số tự nhiên cho một số thập phân

Muốn chia một số tự nhiên cho một số thập phân ta làm như sau:

- Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì viết thêm vào bên phải số bị chia bấy nhiêu chữ số 0.

- Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia các số tự nhiên.

Ví dụ. Đặt tính rồi tính:

a) 57:9,5

b) 99:8,25

Bài giải

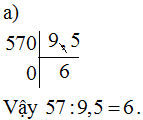
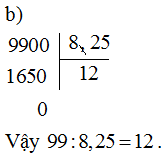
e) Chia một số thập phân cho 0,1; 0,01; 0,001…

Muốn chia một số thập phân cho 0,1; 0,01; 0,001… ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba,… chữ số.

Ví dụ:

$\begin{array}{l}89,13:0,01=8913\\ 213,8:0,1=2138\end{array}$

f) Chia một số thập phân cho một số thập phân

Muốn chia một số thập phân cho một thập phân ta làm như sau:

+ Đếm xem có bao nhiêu chữ số ở phần thập phân của số chia thì chuyển dấu phẩy ở số bị chia sang bên phải bấy nhiêu chữ số.

+ Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia cho số tự nhiên.

Ví dụ. Đặt tính rồi tính:

a) 17,55:3,9

b) 0,3068:0,26

Bài giải

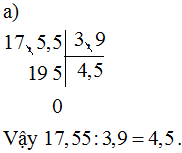
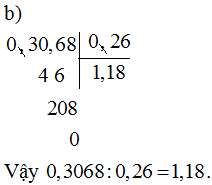
TỈ SỐ PHẦN TRĂM

1. Khái niệm Tỉ số phần trăm

$\frac{a}{100}$ có thể viết dưới dạng là a%, hay $\frac{a}{100}=a\%$

+ Tỉ số phần trăm là tỉ số của hai số mà trong đó ta đưa mẫu của tỉ số về .

+ Tỉ số phần trăm thường được dùng để biểu thị độ lớn tương đối của một lượng này so

với lượng khác.

Ví dụ: $\frac{3}{100}=3\%; \frac{2}{5}=\frac{40}{100}=40\%$

2. Các phép tính với tỉ số phần trăm

a) Phép cộng: $a\%+b\%=\left(a+b\right)\%$

b) Phép trừ: $a\%-b\%=\left(a-b\right)\%$

c) Phép nhân tỉ số phần trăm với một số: $a\%\times b=\left(a\times b\right)\%$

d) Phép chia tỉ số phần trăm cho một số: $a\%:b=\left(a:b\right)\%$

Ví dụ.

a) $12\%+15\%=\left(12+15\right)\%=27\%$ viết gọn $12\%+15\%=27\%$

b) $57\%-13\%=47\%$

c) $13\%\times 3=39\%$

d) $28\%:4=7\%$

3. Các bài toán cơ bản của tỉ số phần trăm

Bài toán 1: Tìm tỉ số phần trăm của hai số

Muốn tìm tỉ số phần trăm của hai số ta làm như sau:

- Tìm thương của hai số đó dưới dạng số thập phân.

- Nhân thương đó với 100 và viết thêm kí hiệu phần trăm (%) vào bên phải tích tìm được

Ví dụ: Tìm tỉ số phần trăm của 315 và 600

Bài giải

Tỉ số phần trăm của 315 và 600 là:

ĐS: 52,5 %

Bài toán 2: Tìm giá trị phần trăm của một số cho trước

Muốn tìm giá trị phần của một số cho trước ta lấy số đó chia cho 100 rồi nhân với số phần trăm hoặc lấy số đó nhân với số phần trăm rồi chia cho 100.

Ví dụ. Trường Đại Từ có 600 học sinh. Số học sinh nữ chiếm 45% số học sinh toàn trường. Tính số học sinh nữ của trường.

Bài giải

Số học sinh của trường đó là:

$600:100\times 45=270$ (học sinh) hoặc $600\times 45:100=270$ (học sinh)

Đáp số: 270 học sinh

Bài toán 3: Tìm một số, biết giá trị một tỉ số phần trăm của số đó

Muốn tìm một số khi biết giá trị phần trăm của số đó ta lấy giá trị phần trăm của số đó chia cho số phần trăm rồi nhân với 100 hoặc ta lấy giá trị phần trăm của số đó nhân với 100 rồi chia cho số phần trăm.

Ví dụ. Tìm một số biết 30% của nó bằng 72.

Bài giải

Giá trị của số đó là:

$72:30\times 100=240$

Đáp số: 240

ĐẠI LƯỢNG VÀ ĐO ĐẠI LƯỢNG

1. Bảng đơn vị đo độ dài

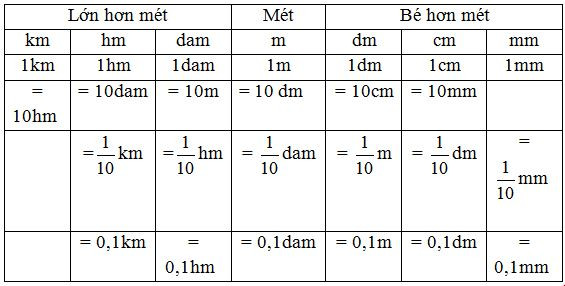
Nhận xét

- Hai đơn vị đo độ dài liền nhau gấp ( hoặc kém) nhau 10 lần.

Ví dụ: $1m=10dm;$$1cm=\frac{1}{10}dm=0,1\text{d}m$

- Mỗi đơn vị đo độ dài ứng với một chữ số.

Ví dụ: $1245m =1km2hm4dam5m$

2. Bảng đơn vị đo khối lượng

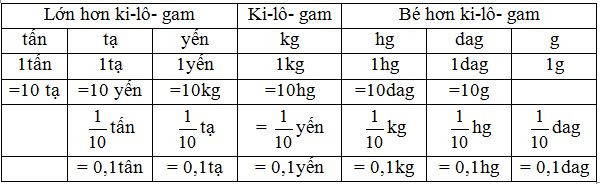
Nhận xét:

- Hai đơn vị đo khối lượng liền nhau gấp (hoặc kém) nhau 10 lần.

- Mỗi đơn vị đo khối lượng ứng với một chữ số.

Ví dụ: 

3. Bảng đơn vị đo diện tích

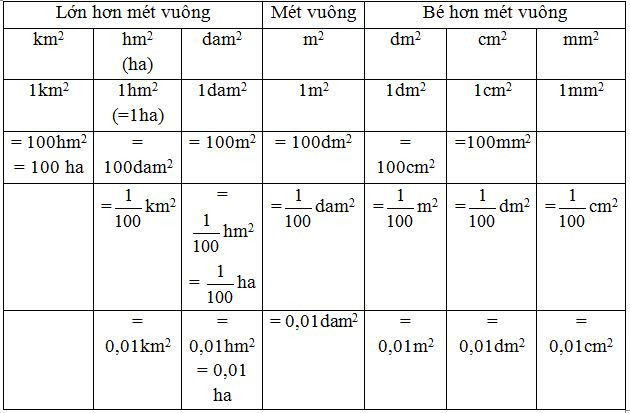
Nhận xét:

- Hai đơn vị đo diện tích liền nhau gấp (hoặc kém) nhau 100 lần.

Ví dụ: $1m^2=100d{m}^2;$$1c{m}^2 =\frac{1}{100}d{m}^2=0,01d{m}^2$

- Mỗi đơn vị đo độ dài ứng với hai chữ số.

Ví dụ: $1245m^2 =12da{m}^{2}45m^2$

4. Bảng đơn vị đo thể tích

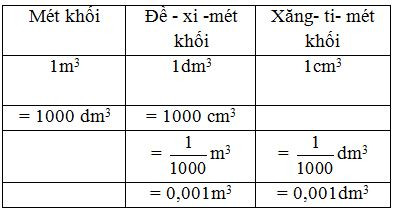
Nhận xét:

- Hai đơn vị đo thể tích liền nhau gấp (hoặc kém) nhau 1000 lần.

Ví dụ: $1m^3=1000d{m}^{3 };$$1c{m}^3 =\frac{1}{1000}d{m}^3=0,001d{m}^3$

-  Mỗi đơn vị đo diện tích ứng với ba chữ số.

Ví dụ: $1245d{m}^3 =1m{}_{3}245d{m}^3$

Lưu ý: 1dm³ = 1 lít

HÌNH TAM GIÁC

1. Hình tam giác

Hình tam giác ABC có:

- Ba cạnh là: cạnh AB, cạnh AC, cạnh BC.

- Ba đỉnh là: đỉnh A, đỉnh B, đỉnh C.

- Ba góc là: 

Góc đỉnh A, cạnh AB và AC (gọi tắt là góc A);

Góc đỉnh B, cạnh BA và BC (gọi tắt là góc B);

Góc đỉnh C, cạnh AC và CB (gọi tắt là góc C).

Vậy hình tam giác có 3 cạnh, 3 góc, 3 đỉnh.

2. Một số loại hình tam giácCó 3 loại hình tam giác:

- Hình tam giác có ba góc nhọn

- Hình tam giác có một góc tù và hai góc nhọn

- Hình tam giác có một góc vuông và hai góc nhọn (gọi là hình tam giác vuông)

*) Hình vẽ minh họa

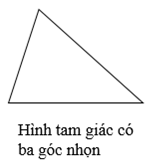
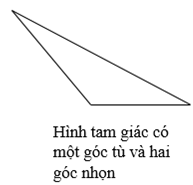
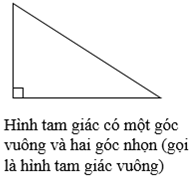
3. Cách xác định đáy và đường cao của hình tam giác

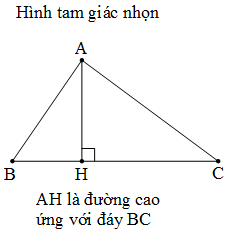
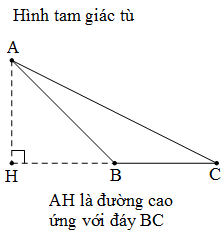
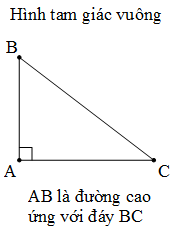
4. Diện tích hình tam giác

Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.

$S = a\times h:2$

Ví dụ. Tính diện tích hình tam giác có độ dài đáy là 13cm và chiều cao là 4cm.

Bài giải

Diện tích hình tam giác đó là:

$13\times 4:2=26\left(c{m}^2\right)$

Đáp số: 26 cm²

HÌNH THANG

1. Định nghĩa: Hình thang có một cặp cạnh đối diện song song.

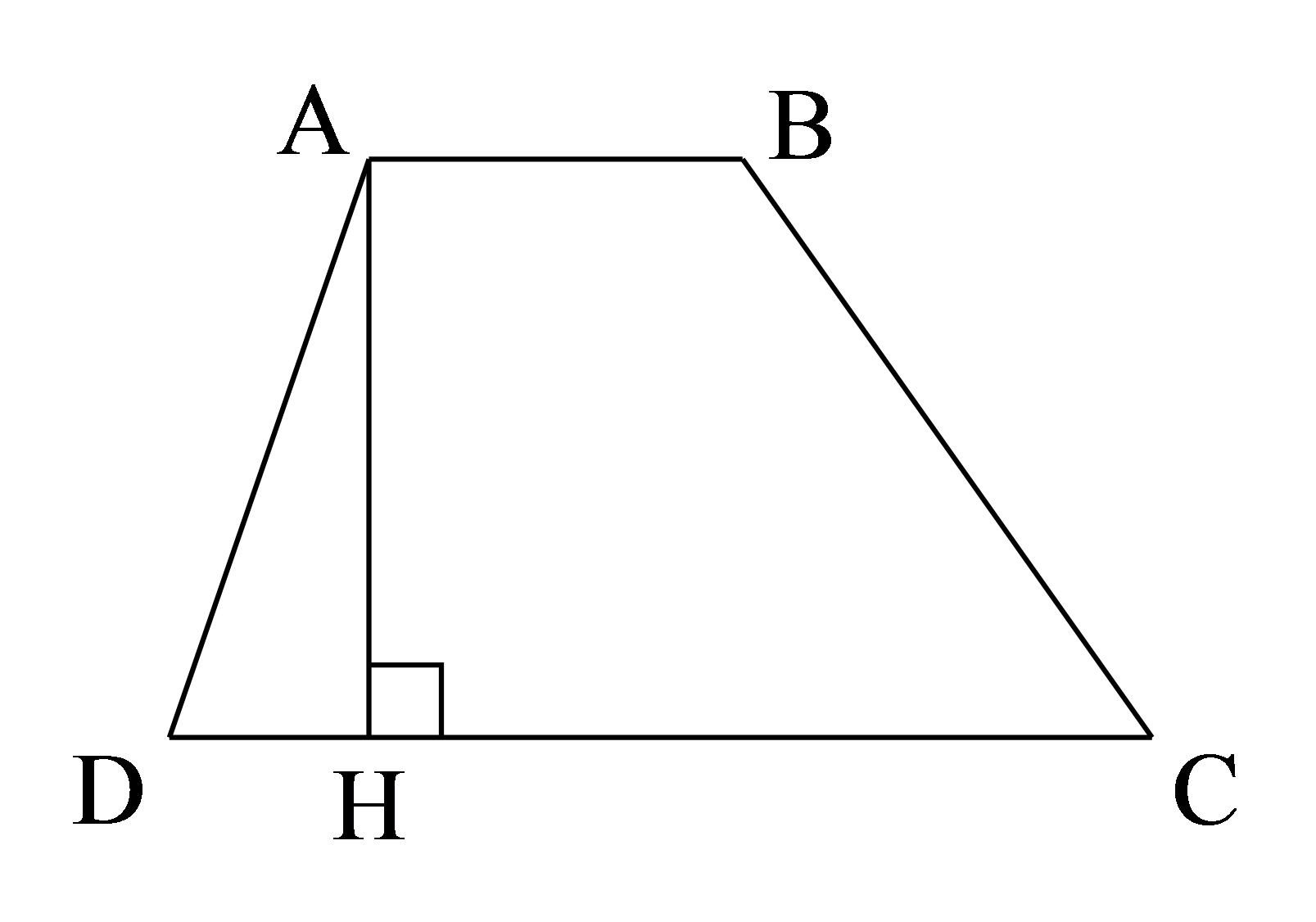Hình thang ABCD có:

Cạnh đáy AB và cạnh đáy DC.  Cạnh bên AD và cạnh bên BC.

AB song song với DC.

AH là đường cao, độ dài AH là chiều cao  

*) Hình thang vuông:

AD vuông góc với hai đáy AB, DC.

AD là đường cao của hình thang của ABCD.

2. Diện tích hình thang: Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.

$S=\left(a+b\right)\times h:2$

Trong đó,

a là đáy nhỏ

b là đáy lớn

h là chiều cao

Ví dụ. Tính diện tích hình thang biết độ dài hai đáy lần lượt là 18cm, 14cm và chiều cao 9cm.

Bài giải

Diện tích hình thang đó là

$\left(18+14\right)\times 9:2=144\left(c{m}^2\right)$

Đáp số: 144cm²

HÌNH TRÒN

1. Hình tròn. Đường tròn.

Vẽ đường tròn tâm O, các điểm A, điểm B, điểm M, điểm C nằm trên đường tròn.

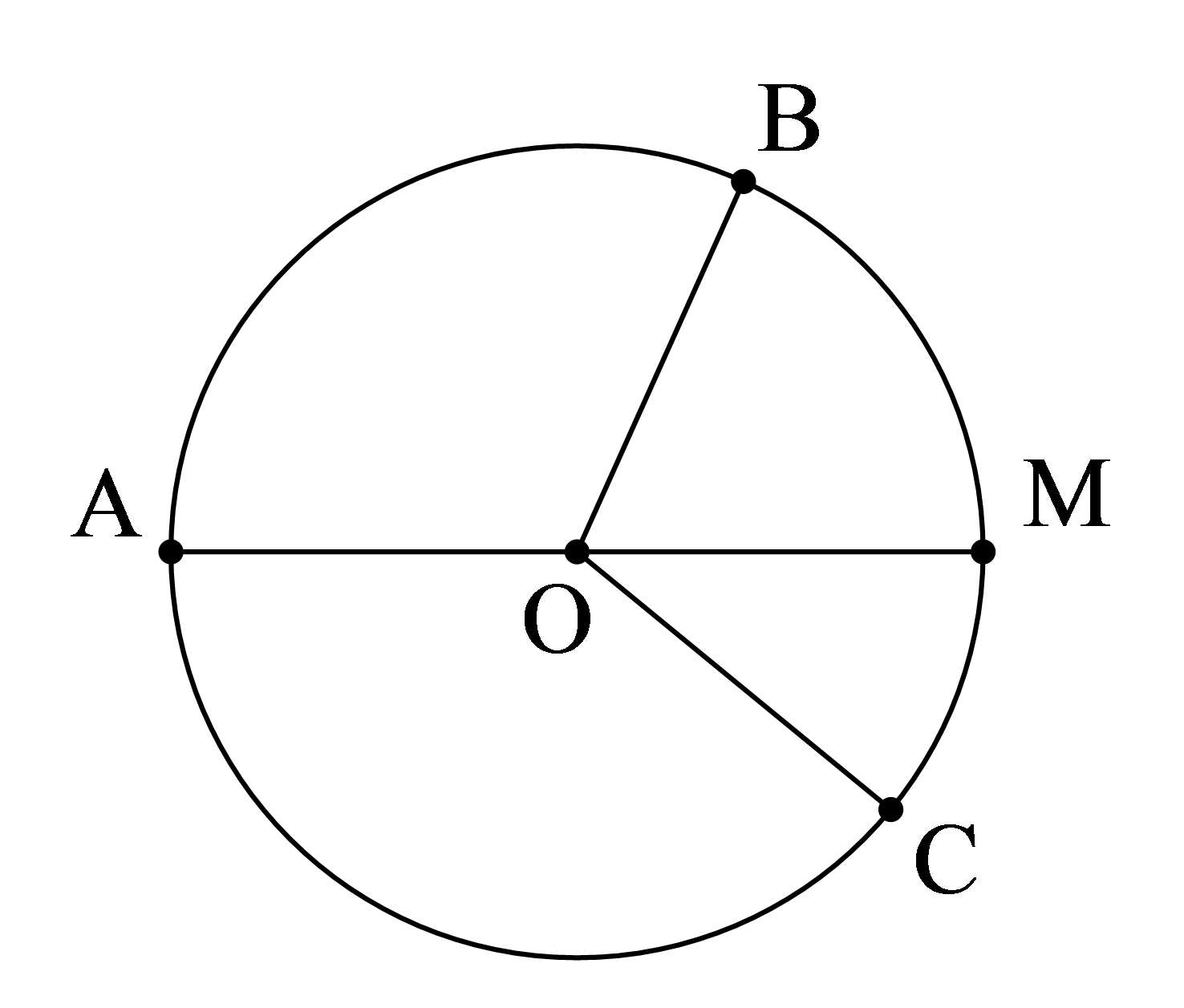
*) Bán kính

- Nối tâm O với một điểm A trên đường tròn. Đoạn thẳng OA là bán kính của đường tròn. Tất cả các bán kính của hình tròn đều bằng nhau OA=OB=OC=OM.

- Bán kính được kí hiệu là r.

*) Đường kính

Đoạn thẳng AM nối hai điểm M, N của đường tròn và đi qua tâm O là đường kính của hình tròn.  

Đường kính được kí hiệu là d

Trong một hình tròn, đường kính dài gấp hai lần bán kính (d=2r)

*) Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong hình tròn đó.

2. Chu vi hình tròn

*) Muốn tính chu vi hình tròn ta lấy đường kính nhân với 3,14:

$C=d\times 3,14$

(C là chu vi hình tròn, d là đường kính hình tròn)

Ví dụ. Tính chu vi hình tròn có đường kính là 8cm

Bài giải

Chu vi hình tròn là:

$8\times 3,14=25,12\left(cm\right)$

Đáp số: 25,12 cm

*) Muốn tính chu vi hình tròn ta lấy 2 lần bán kính nhân với 3,14.

$C=2\times r\times 3,14$

Ví dụ. Tính chu vi hình tròn có bán kính là 3cm

Bài giải

Chu vi hình tròn là:

$3\times 2\times 3,14=18,84\left(cm\right)$

Đáp số: 18,84cm

3. Diện tích hình tròn

Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với 3,14.

$S=r\times r\times 3,14$

(S là diện tích hình tròn, r là bán kính hình tròn)

Ví dụ. Tính diện tích hình tròn có bán kính

Bài giải

Diện tích hình tròn là:

$2\times 2\times 3,14=12,56\left(d{m}^2\right)$

Đáp số: 12,56 dm²

HÌNH HỘP CHỮ NHẬT

1. Định nghĩa

Hình hộp chữ nhật là một hình không gian có 6 mặt đều là hình chữ nhật.

Hai mặt đối diện nhau của hình chữ nhật được xem là hai mặt đáy của hình chữ nhật. Các mặt còn lại đều là mặt bên của hình chữ nhật.

Hình hộp chữ nhật ba chiều: chiều dài, chiều rộng, chiều cao

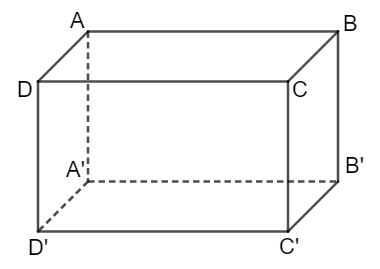
Hình hộp chữ nhật có:

+ 12 cạnh: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’, AA’, BB’, CC’, DD’

+ 8 đỉnh: đỉnh A, đỉnh B, đỉnh C, đỉnh D, đỉnh A’, đỉnh B’, đỉnh C, đỉnh D’

+ 6 mặt: ABCD, BCC’B’, A’B’C’D’, DCD’C’, ADD’C’, ABB’A’.

2. Công thức

Cho hình vẽ:

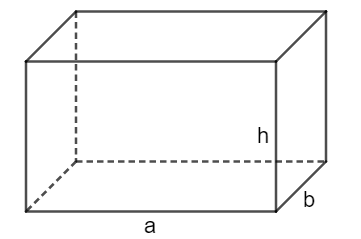
Trong đó:

a: Chiều dài

b: Chiều rộng

h: Chiều cao

2.1. Công thức tính diện tích xung quanh hình hộp chữ nhật

Diện tích xung quanh hình hộp chữ nhật bằng tích của chu vi đáy và chiều cao:

$S_{xq}=\left(a+b\right)\times h\times 2$

Ví dụ: Tính diện tích xung quanh của hình hộp chữ nhật, biết chiều dài 20 m, chiều rộng 7 m, chiều cao 10 m.

Bài giải

Diện tích xung quanh của hình hộp chữ nhật là:

$\left(20+7\right)\times 2\times 10=540\left(c{m}^2\right)$

Đáp số: 540 cm²

2.2. Công thức tính diện tích toàn phần hình hộp chữ nhật

Diện tích toàn phần hình hộp chữ nhật bằng tổng diện tích xung quanh hình hộp chữ nhật và diện tích hai mặt còn lại.

$S_{tp}=S_{xq}+2\times a\times b$

Ví dụ: Một cái thùng hình chữ nhật có chiều cao là 3 cm, chiều dài là 5,4 cm, chiều rộng là 2 cm. Tính diện tích toàn phần của cái thùng đó.

Bài giải

Diện tích xung quanh của hình hộp chữ nhật là:

$\left(5,4+2\right)\times 2\times 3=44,4\left(c{m}^2\right)$

Diện tích đáy của hình hộp chữ nhật là:

$5,4\times 2=10,8\left(c{m}^2\right)$

Diện tích toàn phần của hình hộp chữ nhật là:

$44,4+10,8\times 2=66\left(c{m}^2\right)$

Đáp số: 66m²

2.3. Công thức tính thể tích hình hộp chữ nhật

Thể tích của hình hộp chữ nhật bằng tích của diện tích đáy và chiều cao.

$V=a\times b\times h$

Ví dụ: Tính thể tích hình hộp chữ nhật có chiều dài 9cm, chiều rộng 5cm và chiều cao .

Bài giải

Thể tích của hình hộp chữ nhật là:

$9\times 5\times 6=270\left(c{m}^3\right)$

Đáp số: 270 cm³

HÌNH LẬP PHƯƠNG

1. Định nghĩa

Hình lập phương là hình khối có chiều rộng, chiều dài và chiều cao đều bằng nhau.

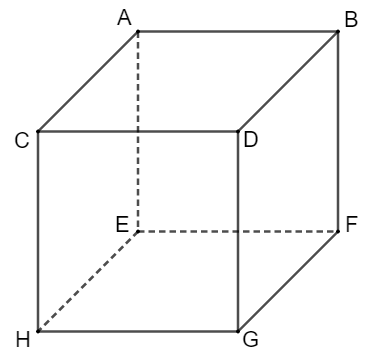
Hình lập phương có:

+ 8 đỉnh: đỉnh A, đỉnh C, đỉnh B, đỉnh D, đỉnh E, đỉnh F, đỉnh G, đỉnh H

+ 12 cạnh bằng nhau: AB = BD = DC = CA = CH = AE = DG = BF = FG = FE = EH = HG

+ 6 mặt là hình vuông bằng nhau

2. Công thức

Cho hình vẽ:

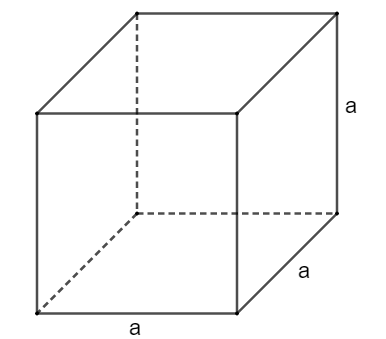
Trong đó: a là độ dài cạnh của hình lập phương

2.1. Công thức tính diện tích xung quanh hình lập phương

Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 4.

$S_{xq}=a\times a\times 4$

Ví dụ: Tính diện tích xung quanh của hình lập phương có cạnh 6cm.

Bài giải

Diện tích xung quanh của hình lập phương là:

$6\times 6\times 4=144\left(c{m}^2\right)$

Đáp số: $144c{m}^2$

2.2. Công thức tính diện tích toàn phần hình lập phương

Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân với 6.

$S_{tp}=a\times a\times 6$

Ví dụ: Tính diện tích toàn phần của hình lập phương có cạnh 5cm.

Bài giải

Diện tích toàn phần của hình lập phương đó là:

$5\times 5\times 6=150\left(c{m}^2\right)$

Đáp số: 150 cm²

2.3. Công thức tính thể tích hình lập phương

Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh nhân rồi nhân với cạnh.

$V=a\times a\times a$

Ví dụ: Tính thể tích lập phương có cạnh 3 cm.

Bài giải

Thể tích của hình hộp chữ nhật là:

$3\times 3\times 3=27\left(c{m}^3\right)$

Đáp số: 270cm³

SỐ ĐO THỜI GIAN – CHUYỂN ĐỘNG ĐỀU

1. Bảng đơn vị đo thời gian

Các đơn vị đo thời gian

Tháng 1, 3, 5, 7, 8, 10, 12 có 31 ngày.

Tháng 4, 6, 9, 11 có 30 ngày.

Tháng 2 có 28 ngày (vào năm nhuận có 29 ngày)

Ví dụ:  

+) Một năm rưỡi = 1,5 năm = 12 tháng × 1,5 = 1,8 tháng

+) $\frac{2}{3}$ giờ = 60 phút $\times \frac{2}{3}$ = 40 phút

+) 0,5 giờ = 60 phút × 0,5 = 30 phút

+) 216 phút = 3 giờ 36 phút = 3,6 giờ (thực hiện phép chia 216 cho 60)

2. Phép toán với số đo thời gian

a) Cộng số đo thời gian

Phương pháp:

- Đặt tính thẳng hàng và thực hiện tính như đối với phép cộng các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số đo thời gian ở đơn vị bé có thể chuyển đổi sang đơn vị lớn thì ta thực hiện chuyển đổi sang đơn vị lớn hơn.

Ví dụ. Đặt tính rồi tính:

a) 2 giờ 15 phút + 4 giờ 22 phút

b) 5 phút 38 giây + 3 phút 44 giây

Bài giải

a) 

Vậy 2 giờ 15 phút + 4 giờ 22 phút = 6 giờ 37 phút

b)

8 phút 82 giây = 9 phút 22 giây (82 giây = 1 phút 22 giây)

Vậy 5 giờ 38 giây + 3 giờ 44 giây = 9 phút 22 giây

b) Trừ số đo thời gian

Phương pháp:

- Đặt tính thẳng hàng và thực hiện tính như đối với phép trừ các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số đo theo đơn vị nào đó ở số bị trừ bé hơn số đo tương ứng ở số trừ thì cần chuyển đổi 1 đơn vị hàng lớn hơn liền kề sang đơn vị nhỏ hơn rồi thực hiện phép trừ như bình thường.

Ví dụ. Đặt tính rồi tính:

a) 9 giờ 45 phút – 3 giờ 12 phút

b) 14 phút 15 giây – 8 phút 39 giây

Bài giải

a)

b)

đổi thành 

c) Nhân số đo thời gian

Phương pháp:

- Đặt tính thẳng hàng và thực hiện tính như đối với phép nhân các số tự nhiên.

- Khi tính sau mỗi kết quả ta phải ghi đơn vị đo tương ứng.

- Nếu số đo thời gian ở đơn vị bé ta có thể chuyển đổi sang đơn vị lớn thì ta thực hiện chuyển đổi sang đơn vị lớn hơn.

Ví dụ. Đặt tính rồi tính:

a)     3 giờ 12 phút × 3

b)    5 năm 9 tháng × 2

Bài giải

a)

b)

(18 tháng = 1 năm 6 tháng)

Vậy 5 năm 9 tháng × 2 = 11 năm 6 tháng.

TOÁN CHUYỂN ĐỘNG ĐỀU

1.  Vận tốc: Muốn tính vận tốc ta lấy quãng đường chia cho thời gian.

v = s  : t

2.  Quãng đường: Muốn tính quãng đường ta lấy vận tốc nhân với thời gian.

s  =   v  × t

3.  Thời gian: Muốn tính thời gian ta lấy quãng đường chia cho vận tốc

t = s : v

Hai chuyển động ngược chiều gặp nhau

a) Tìm tổng vận tốc của hai chuyển động 

$\left(v_1+v_2\right)=s:t$

b) Tìm quãng đường của hai chuyển động

$s=\left(v_1+v_2\right)\times t$

c) Tìm thời gian của hai chuyển động

$t=s:\left(v_1+v_2\right)$

Ví dụ. Cùng một lúc, ô tô đi từ A đến B với vận tốc là 50km/giờ và xe máy đi từ B đến A với vận tốc là 36km/giờ. Biết độ dài quãng đường AB là 215km. Hỏi kể từ lúc bắt đầu đi, sau mấy giờ hai xe đó gặp nhau?

Bài giải

Tổng vận tốc của hai xe là:

50 + 36 = 86 (km/giờ)

Thời gian đi để hai xe gặp nhau là:

215 : 86 = 2,5 (giờ)

Đáp số: 2,5 giờ

Hai chuyển động cùng chiều gặp nhau

a) Tìm hiệu vận tốc của hai chuyển động

$\left(v_1-v_2\right)=s:t$

b) Tìm quãng đường của hai chuyển động

$s=\left(v_1-v_2\right)\times t$

c) Tìm thời gian của hai chuyển động

$t=s:\left(v_1-v_2\right)$

Ví dụ. Cùng một lúc, ô tô đi từ A đến B với vận tốc 50km/giờ đuổi theo một xe máy đi từ B đến C với vận tốc là 38km/giờ. Biết độ dài quãng đường AB là 18km. Hỏi kể từ lúc bắt đầu đi, sau mấy giờ ô tô đuổi kịp xe máy?

Bài giải

Hiệu vận tốc của hai xe là:

50 – 38 = 12 (km/giờ)

Thời gian đi để ô tô đuổi kịp xe máy là:

18 : 12 = 1,5 (giờ)

Đáp số: 1,5 giờ

Chuyển động trên dòng nước

*)  Một số kiến thức cần nhớ

Vận tốc thực của thuyền = (vận tốc xuôi dòng + vận tốc ngược dòng) : 2

Vận tốc dòng nước = (vận tốc xuôi dòng – vận tốc ngược dòng) : 2

Vận tốc xuôi dòng – vận tốc ngược dòng = vận tốc dòng nước × 2

* Chú ý

Vận tốc thực của thuyền chính là vận tốc của thuyền khi dòng nước đứng yên (hay dòng nước yên lặng).

Trên cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.

Ví dụ. Vận tốc ca nô khi nước lặng là 25km/giờ. Vận tốc dòng nước là 3km/giờ. Tính:

a) Vận tốc của ca nô khi đi xuôi dòng.

b) Vận tốc của ca nô khi đi ngược dòng

Bài giải

a) Vận tốc của ca nô khi đi xuôi dòng là:

25 + 3 = 28 (km/giờ)

b) Vận tốc của ca nô khi đi ngược dòng là:

25 – 3 = 22 (km/giờ)

Đáp số:

a) 28 km/giờ

b) 22 km/giờ

Xem thêm các bài tổng hợp lý thuyết Toán lớp 5 đầy đủ, chi tiết khác:

Lý thuyết Ôn tập: So sánh hai phân số

Lý thuyết Ôn tập: So sánh hai phân số (tiếp theo)

Lý thuyết Phân số thập phân

Lý thuyết Ôn tập: Phép cộng và phép trừ hai phân số

Lý thuyết Ôn tập: Phép nhân và phép chia hai phân số