25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ứng dụng của tích phân có đáp án (Phần 1)

Trắc nghiệm Ứng dụng của tích phân có đáp án (Phần 1)

Đề số 1

Trắc nghiệm Ứng dụng của tích phân có đáp án (Phần 1)

811 lượt thi
25 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x $(1 \leq x \leq 3)$ thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và $\sqrt{3 x^{2} - 2}$

A. $V = 32 + 2 \sqrt{15}$

B. $V = \frac{124 π}{3}$

C. $V = \frac{124}{3}$

D. $V = (32 + 2 \sqrt{15}) π$

Câu 2:

Thể tích vật thể nằm giữa hai mặt phẳng x = 0 và x = 2, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x $(0 \leq x \leq 2)$ là một nửa đường tròn đường kính bằng:

A. $2 π$

B. $5 π$

C. $4 π$

D. $3 π$

Câu 3:

Cho hình phẳng giới hạn bởi $D = \{y = \tan x; y = 0; x = 0; x = \frac{π}{3}\}$ . Thể tích vật tròn xoay khi D quay quanh trục Ox là: $V = π (a - \frac{π}{b})$ với $a, b \in R$ . Tính $T = a^{2} + 2 b$

A. T = 6

B. T = 9

C. T = 12

D. T = 3

Câu 4:

Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi đường tròn có phương trình $x^{2} + y^{2} = 1$ và mỗi thiết diện vuông góc với trục Ox là một hình vuông (tham khảo hình bên)

A. $\frac{16}{3}$

B. $\frac{14}{3}$

C. $\frac{17}{3}$

D. $\frac{13}{3}$

Câu 5:

Cho hình phẳng (H) giới hạn bởi parabol $y = a x^{2} + 1 (a > 0),$ trục tung và đường thẳng x = 1. Quay (H) quanh trục Ox được một khối tròn xoay có thể tích bằng $\frac{28}{15} π$ . Mệnh đề nào dưới đây đúng?

A. 2 < a < 3

B. 0 < a < 2

C. 5 < a < 8

D. 3 < a < 5

Câu 6:

Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y=tanx, trục Ox, đường thẳng x = 0, đường thẳng $x = \frac{π}{3}$ quanh trục Ox là:

A. $V = \sqrt{3} - \frac{π}{3}$

B. $V = \sqrt{3} + \frac{π}{3}$

C. $V = π \sqrt{3} + \frac{π^{2}}{3}$

D. $V = π \sqrt{3} - \frac{π^{2}}{3}$

Câu 7:

Tính thể tích khi $S = \{y = x^{2} - 4 x + 6; y = - x^{2} - 2 x + 6\}$ quay quanh trục Ox

A. 3

B. $\frac{π}{3}$

C. $π$

D. $3 π$

Câu 8:

Gọi H là hình phẳng giới hạn bởi parabol $y = x^{2}$ và đường thẳng y = 2x. Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành

A. $V = \frac{64 π}{15}$

B. $V = \frac{16 π}{15}$

C. $V = \frac{20 π}{3}$

D. $V = \frac{4 π}{3}$

Câu 9:

Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a; b] với a < b. Kí hiệu $S_{1}$ là diện tích hình phẳng giới hạn bởi các đường y = 3f(x), y = 3g(x), x = a, x = b, $S_{2}$ là diện tích hình phẳng giới hạn bởi các đường y = f(x) − 2, y = g(x) − 2, x = a, x = b. Khẳng định nào sau đây đúng?

A. $S_{1} = 2 S_{2} - 2$

B. $S_{1} = 2 S_{2} + 2$

C. $S_{1} = 2 S_{2}$

D. $S_{1} = 3 S_{2}$

Câu 10:

Thể tích khối tròn xoay sinh ra bởi phép quay xung quanh Ox của hình giới hạn bởi trục Ox và parabol (P): $y = x^{2} - a x$ (a>0) bằng V = 2. Khẳng định nào dưới đây đúng?

A. $a \in (\frac{1}{2}; 1)$

B. $a \in (1; \frac{3}{2})$

C. $a \in (\frac{3}{2}; 2)$

D. $a \in (2; \frac{5}{2})$

Câu 11:

Cho hai hàm số $y = f_{1} (x)$ và $y = f_{2} (x)$ liên tục trên đoạn [a;b] và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x = a, x = b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây?

A. $V = π \int_{a}^{b} ({f_{1}}^{2} (x) - {f_{2}}^{2} (x)) dx$

B. $V = π \int_{a}^{b} (f_{1} (x) - f_{2} (x)) dx$

C. $V = \int_{a}^{b} ({f_{1}}^{2} (x) - {f_{2}}^{2} (x)) dx$

D. $V = π \int_{a}^{b} {(f_{1} (x) - f_{2} (x))}^{2} dx$

Câu 12:

Cho hai hàm số $f (x) = m x^{3} + n x^{2} + p x - \frac{5}{2}$ (m, n, p thuộc R) và $g (x) = x^{2} + 2 x - 1$ có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là −3; −1; 1( tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số f(x)và g(x) bằng

A. $\frac{9}{2}$

B. $\frac{18}{5}$

C. 4

D. 5

Câu 13:

Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh 40(cm) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình $4 x^{2} = y^{4}$ và $4 (| x | - 1)^{3} = y^{2}$ để tạo hoa văn cho viên gạch. Diện tích phần màu vàng gần nhất với giá trị nào dưới đây?

A. 506 $(c m^{2})$

B. 747 $(c m^{2})$

C. 507 $(c m^{2})$

D. 746 $(c m^{2})$

Câu 14:

Cho hàm số $y = x^{4} - 3 x^{2} + m$ có đồ thị là $(C_{m})$ (m là tham số thực). Giả sử $(C_{m})$ cắt trục Ox tại 4 điểm phân biệt. Gọi $S_{1}, S_{2}$ là diện tích của hai hình phẳng nằm dưới trục Ox và $S_{3}$ là diện tích của hình phẳng nằm trên trục Ox được tạo bởi $(C_{m})$ với trục Ox. Biết rằng tồn tại duy nhất giá trị $m = \frac{a}{b}$ (với a, b thuộc N* và tối giản) để $S_{1} + S_{2} = S_{3}$ . Giá trị của 2a − b bằng:

A. 3

B. -4

C. 6

D. -2

Câu 15:

Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là $S_{1}$ và $S_{2}$ (tham khảo hình vẽ).

Tỉ số $\frac{S_{1}}{S_{2}}$ bằng:

A. $\frac{1}{2}$

B. $\frac{3}{5}$

C. $\frac{2}{5}$

D. $\frac{1}{3}$

Câu 16:

Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh A, B, C, D và hai đường parabol có các đỉnh lần lượt là E, F (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng AB, đối xứng với nhau qua trục CD, hai parabol cắt elip tại các điểm M, N, P, Q. Biết AB = 8m, CD = 6m, $M N = P Q = 3 \sqrt{3} m$ , EF = 2m. Chi phí để trồng hoa trên vườn là $300.000 đ / m^{2}$ . Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây

A. 4.477.800 đồng

B. 4.477.000 đồng

C. 4.477.815 đồng

D. 4.809.142 đồng

Câu 17:

Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(−1) > 0 > f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = 1 và x = −1. Mệnh đề nào sau đây là đúng?

A. $S = \int_{0}^{- 1} f (x) d x + \int_{0}^{1} |f (x)| d x$

B. $S = \int_{- 1}^{1} |f (x)| d x$

C. $S = \int_{- 1}^{1} f (x) d x$

D. $S = |\int_{- 1}^{1} f (x) d x|$

Câu 18:

Cho parabol (P) có đồ thị như hình vẽ:

Tính diện tích giới hạn bởi (P) và trục hoành.

A. $\frac{8}{3}$

B. $\frac{4}{3}$

C. 4

D. 2

Câu 19:

Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y = x^{2} - 2 x$ và $y = - x^{2} + 4 x$

A. 12

B. 9

C. $\frac{11}{3}$

D. 27

Câu 20:

Tính diện tích hình phẳng giới hạn bởi hai đường: $y = | x^{2} - 4 x + 3 |; y = x + 3$

A. $\frac{107}{6}$

B. $\frac{109}{6}$

C. $\frac{109}{7}$

D. $\frac{109}{8}$

Câu 21:

Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số $y = x^{2} - 4 x + 4$ , trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua A (0; 4) có hệ số góc k chia (H) thành 2 phần có diện tích bằng nhau là

A. K = -6

B. K = -2

C. K = -8

D. K = -4

Đáp án đúng là A

Lời giải

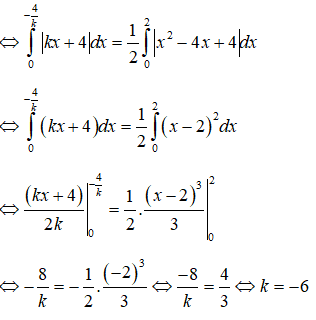
*Phương pháp giải:

Cho hai hàm số $y = f (x)$ và $y = g (x)$ liên tục trên $[a; b]$ . Khi đó thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi hai đồ thị số $y = f (x)$ , $y = g (x)$ và hai đường thẳng $x = a; y = b$ quanh trục $O x$ là:

$V = π \int_{a}^{b} | f^{2} (x) - g^{2} (x) | d x$

*Lý thuyết:

Khối tròn xoay là một khối hình được tạo bằng cách quay một mặt phẳng quanh một trục cố định. Trong chương trình toán học phổ thông các bạn sẽ được tiếp xúc với một số khối tròn xoay như khối nón tròn xoay, khối trụ tròn xoay, khối cầu tròn xoay,...

2. Công thức tính thể tích khối tròn xoay

* Quay quanh trục Ox:

Hình giới hạn bởi đường cong y = f(x), trục Ox và hai đường thẳng x = a, x = b (trong đó f(x) liên tục trên đoạn [a;b]) quay quanh trục Ox, ta được khối tròn xoay.

Thể tích của khối tròn xoay được tính theo công thức: $V = π \int_{a}^{b} {[f (x)]}^{2} d x$

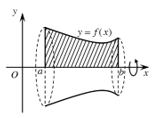
Hình giới hạn bởi hai đường cong y = f(x), y = g(x) và hai đường thẳng x = a, x = b (trong đó f(x), g(x) liên tục trên đoạn [a;b]) quay quanh trục Ox.

Thể tích của khối tròn xoay được tính theo công thức: $V = π \int_{a}^{b} |f^{2} (x) - g^{2} (x)| d x$

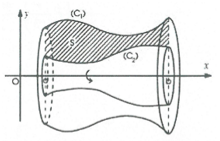
* Quay quanh trục Oy:

Hình giới hạn bởi đường cong x = f(y), trục Oy và hai đường thẳng y = c; y = d (trong đó f(x) liên tục trên đoạn [c; d]) quay quanh trục Oy, ta được khối tròn xoay.

Thể tích của khối tròn xoay được tính theo công thức: $V = π \int_{a}^{b} {[f (y)]}^{2} d y$

Xem thêm

Công thức tính thể tích khối tròn xoay (đầy đủ, chính xác nhất)

50 bài toán về ứng dụng của tích phân tính thể tích khối tròn xoay (có đáp án 2024) – Toán 12

Câu 22:

Ông B có một khu vườn giới hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ Oxy như hình vẽ bên thì parabol có phương trình $y = x^{2}$ và đường thẳng là y = 25. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua O và điểm M trên parabol để trồng hoa. Hãy giúp ông B xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vường nhỏ bằng 92.

A. $O M = 2 \sqrt{5}$

B. $O M = 3 \sqrt{10}$

C. OM = 15

D. OM = 10

Câu 23:

Cho (H) là hình phẳng giới hạn bởi parabol $y = \sqrt{3} x^{2}$ , cung tròn có phương trình $y = \sqrt{4 - x^{2}}$ (với 0 ≤ x ≤ 2) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

A. $\frac{4 π + \sqrt{3}}{12}$

B. $\frac{4 π - \sqrt{3}}{6}$

C. $\frac{4 π + 2 \sqrt{3} - 3}{6}$

D. $\frac{5 \sqrt{3} - 2 π}{3}$

Câu 24:

Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y = - x^{2} + 2 x + 1$ và $y = 2 x^{2} - 4 x + 1$ là:

A. 4

B. 5

C. 8

D. 10

Câu 25:

Diện tích S của hình phẳng giới hạn bởi các đường $y = - x^{2} + 2 x, y = - 3, x = 1, x = 2$ được tính bởi công thức nào dưới đây?

A. $S = π \int_{1}^{2} {(- x^{2} + 2 x + 3)}^{2} dx$

B. $S = \int_{1}^{2} (- x^{2} + 2 x - 3) dx$

C. $S = \int_{1}^{2} (- x^{2} + 2 x + 3) dx$

D. $S = \int_{1}^{2} (x^{2} - 2 x - 3) dx$

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương