Câu hỏi:
22/11/2024 981Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y=x2-4x+4, trục tung, trục hoành. Giá trị của k để đường thẳng d đi qua A (0; 4) có hệ số góc k chia (H) thành 2 phần có diện tích bằng nhau là
A. K = -6
B. K = -2
C. K = -8
D. K = -4
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là A
Lời giải
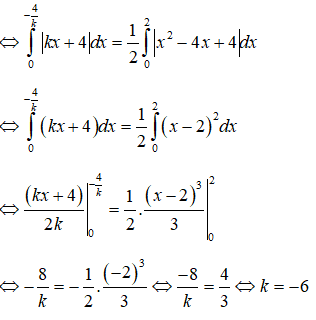
*Phương pháp giải:
Cho hai hàm số y = f(x) và y = g(x) liên tục trên [a;b]. Khi đó thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi hai đồ thị số y = f(x), y = g(x) và hai đường thẳng x = a; y = b quanh trục Ox là:
V= π∫ba|f2(x)−g2(x)|dx
*Lý thuyết:
Khối tròn xoay là một khối hình được tạo bằng cách quay một mặt phẳng quanh một trục cố định. Trong chương trình toán học phổ thông các bạn sẽ được tiếp xúc với một số khối tròn xoay như khối nón tròn xoay, khối trụ tròn xoay, khối cầu tròn xoay,...
2. Công thức tính thể tích khối tròn xoay
* Quay quanh trục Ox:
Hình giới hạn bởi đường cong y = f(x), trục Ox và hai đường thẳng x = a, x = b (trong đó f(x) liên tục trên đoạn [a;b]) quay quanh trục Ox, ta được khối tròn xoay.
Thể tích của khối tròn xoay được tính theo công thức: V=πb∫a[f(x)]2dx
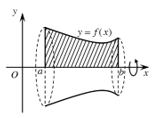
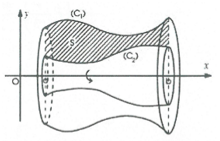
Hình giới hạn bởi hai đường cong y = f(x), y = g(x) và hai đường thẳng x = a, x = b (trong đó f(x), g(x) liên tục trên đoạn [a;b]) quay quanh trục Ox.
Thể tích của khối tròn xoay được tính theo công thức: V=πb∫a|f2(x)−g2(x)|dx
* Quay quanh trục Oy:
Hình giới hạn bởi đường cong x = f(y), trục Oy và hai đường thẳng y = c; y = d (trong đó f(x) liên tục trên đoạn [c; d]) quay quanh trục Oy, ta được khối tròn xoay.
Thể tích của khối tròn xoay được tính theo công thức: V=πb∫a[f(y)]2dy
Xem thêm
Công thức tính thể tích khối tròn xoay (đầy đủ, chính xác nhất)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Gọi H là hình phẳng giới hạn bởi parabol y=x2 và đường thẳng y = 2x. Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành
Câu 2:
Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y=x2-2x và y=-x2+4x
Câu 3:
Cho hình phẳng (H) giới hạn bởi paraboly=ax2+1(a>0), trục tung và đường thẳng x = 1. Quay (H) quanh trục Ox được một khối tròn xoay có thể tích bằng 2815π. Mệnh đề nào dưới đây đúng?
Câu 4:
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1≤x≤3) thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và √3x2-2
Câu 5:
Diện tích S của hình phẳng giới hạn bởi các đường y=-x2+2x,y=-3,x=1,x=2 được tính bởi công thức nào dưới đây?
Câu 6:
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là S1 và S2 (tham khảo hình vẽ).
Tỉ số S1S2 bằng:
Câu 7:
Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(−1) > 0 > f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = 1 và x = −1. Mệnh đề nào sau đây là đúng?
Câu 8:
Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y=tanx, trục Ox, đường thẳng x = 0, đường thẳng x=π3 quanh trục Ox là:
Câu 9:
Ông B có một khu vườn giới hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ Oxy như hình vẽ bên thì parabol có phương trình y=x2 và đường thẳng là y = 25. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua O và điểm M trên parabol để trồng hoa. Hãy giúp ông B xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vường nhỏ bằng 92.
Câu 10:
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a; b] với a < b. Kí hiệu S1 là diện tích hình phẳng giới hạn bởi các đường y = 3f(x), y = 3g(x), x = a, x = b, S2 là diện tích hình phẳng giới hạn bởi các đường y = f(x) − 2, y = g(x) − 2, x = a, x = b. Khẳng định nào sau đây đúng?
Câu 11:
Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi đường tròn có phương trình x2+y2=1 và mỗi thiết diện vuông góc với trục Ox là một hình vuông (tham khảo hình bên)
Câu 13:
Cho hàm số có đồ thị là (m là tham số thực). Giả sử cắt trục Ox tại 4 điểm phân biệt. Gọi là diện tích của hai hình phẳng nằm dưới trục Ox và là diện tích của hình phẳng nằm trên trục Ox được tạo bởi với trục Ox. Biết rằng tồn tại duy nhất giá trị (với a, b thuộc N* và tối giản) để . Giá trị của 2a − b bằng:
Câu 14:
Cho parabol (P) có đồ thị như hình vẽ:
Tính diện tích giới hạn bởi (P) và trục hoành.


