Trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường tròn (Phần 2) có đáp án
Trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường tròn (Phần 2) có đáp án (Vận dụng)
-
922 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Với giá trị nào của m thì đường thẳng ∆: 4x + 3y + m = 0 tiếp xúc với đường tròn (C): x2 + y2 – 9 = 0?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Đường tròn (C) có tâm O(0; 0), bán kính R = 3.
Vì ∆ tiếp xúc với (C) nên ta có d(O, ∆) = R.
\( \Leftrightarrow \frac{{\left| {4.0 + 3.0 + m} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 3\)
⇔ |m| = 15
⇔ m = 15 hoặc m = –15.
Vậy m = 15 hoặc m = –15 thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án D.
Câu 2:
23/07/2024Cho đường tròn (C): x2 + y2 – 4x – 6y + 5 = 0. Đường thẳng d đi qua điểm A(3; 2) và cắt (C) theo một dây cung ngắn nhất có phương trình là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
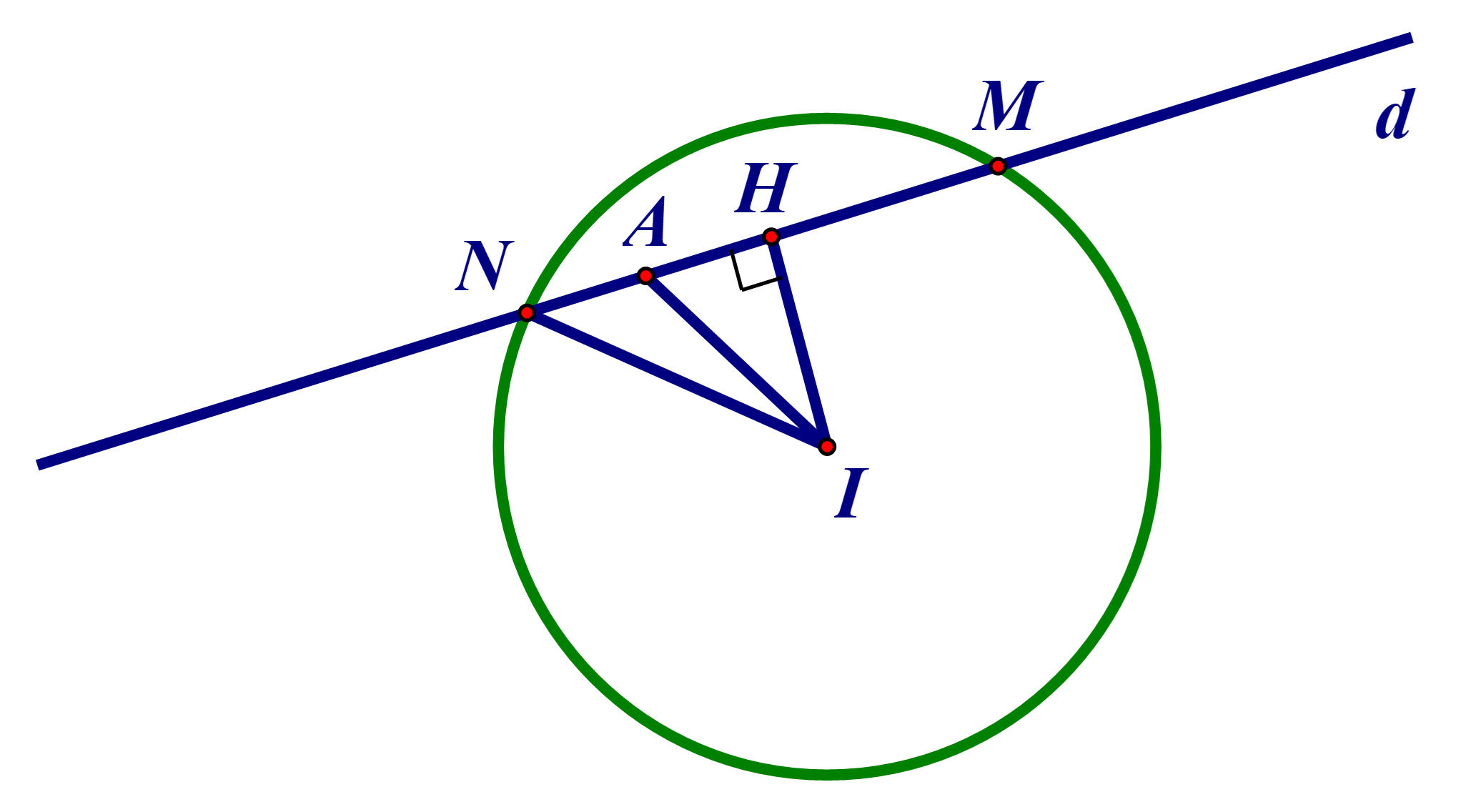
Đường tròn (C) có tâm I(2; 3), bán kính \(R = 2\sqrt 2 \).
Gọi M, N là giao điểm của đường thẳng d và đường tròn (C).
Kẻ IH ⊥ d. Suy ra H là trung điểm MN. Khi đó \(HN = \frac{1}{2}MN\).
∆IHN vuông tại H: IN2 = IH2 + HN2 (Định lí Pytago)
\( \Leftrightarrow {R^2} = I{H^2} + {\left( {\frac{{MN}}{2}} \right)^2}\)
\( \Leftrightarrow {\left( {\frac{{MN}}{2}} \right)^2} = {R^2} - I{H^2}\)
Dây cung MN ngắn nhất khi và chỉ khi IH lớn nhất. Tức là IA ≡ IH hay A ≡ H.
Khi đó IA ⊥ d.
Suy ra d nhận \(\overrightarrow {IA} = \left( {1; - 1} \right)\) làm vectơ pháp tuyến.
Đường thẳng d đi qua A(3; 2) và có vectơ pháp tuyến \(\overrightarrow {IA} = \left( {1; - 1} \right)\).
Suy ra phương trình d: 1(x – 3) – 1(y – 2) = 0
⇔ x – y – 1 = 0.
Vậy ta chọn phương án C.
Câu 3:
22/07/2024Cho đường tròn (C): x2 + y2 + 2x – 6y + 5 = 0. Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y – 15 = 0 là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đường tròn (C) có tâm I(–1; 3), bán kính \(R = \sqrt {{{\left( { - 1} \right)}^2} + {3^2} - 5} = \sqrt 5 \).
Gọi ∆ là tiếp tuyến cần tìm.
Đường thẳng d có vectơ pháp tuyến \({\vec n_d} = \left( {1;2} \right)\).
Vì ∆ // d nên ∆ nhận \({\vec n_d} = \left( {1;2} \right)\) làm vectơ pháp tuyến.
Suy ra phương trình ∆ có dạng: x + 2y + c = 0.
Vì d là tiếp tuyến của (C) nên d(I, ∆) = R.
\( \Leftrightarrow \frac{{\left| { - 1 + 2.3 + c} \right|}}{{\sqrt {{1^2} + {2^2}} }} = \sqrt 5 \)
⇔ |c + 5| = 5
⇔ c + 5 = 5 hoặc c + 5 = –5
⇔ c = 0 hoặc c = –10.
Vậy có 2 phương trình tiếp tuyến d thỏa mãn yêu cầu bài toán có phương trình là: x + 2y = 0 hoặc x + 2y – 10 = 0.
Do đó ta chọn phương án A.
Câu 4:
23/11/2024Đường tròn (C) đi qua hai điểm A(1; 3), B(3; 1) và có tâm nằm trên đường thẳng d: 2x – y + 7 = 0 có phương trình là:
Xem đáp án
Đáp án đúng là: B
Lời giải
Gọi I(a; b) là tâm của đường tròn (C).
Ta có IA2 = IB2 = R2.
\( \Leftrightarrow {\left( {1 - a} \right)^2} + {\left( {3 - b} \right)^2} = {\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2}\)
⇔ 4a = 4b
⇔ a = b.
Khi đó tọa độ I(a; a).
Vì I(a; a) ∈ d nên 2a – a + 7 = 0
⇔ a = –7.
Suy ra I(–7; –7).
Ta có \(R = IA = \sqrt {{{\left( {1 + 7} \right)}^2} + {{\left( {3 + 7} \right)}^2}} = 2\sqrt {41} \).
Vậy phương trình đường tròn (C): (x + 7)2 + (y + 7)2 = 164.
*Phương pháp giải:
1.Gọi I là tâm dựa vào hàm số đè bài để tìm I
2.Suy ra r và viết phương trình đường tròn
*Lý thuyết:
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
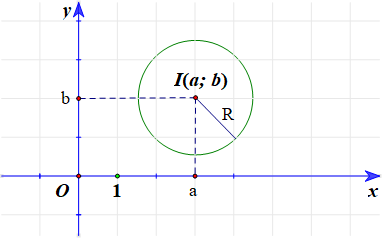Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạoCâu 5:
19/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Phương trình (Cm) có dạng: x2 + y2 – 2ax – 2y + c = 0, với \(\left\{ \begin{array}{l} - 2a = m + 2\\ - 2b = - \left( {m + 4} \right)\\c = m + 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{{m + 2}}{2}\\b = \frac{{m + 4}}{2}\\c = m + 1\end{array} \right.\)
Để (Cm) là phương trình đường tròn thì a2 + b2 – c > 0.
\( \Leftrightarrow {\left( { - \frac{{m + 2}}{2}} \right)^2} + {\left( {\frac{{m + 4}}{2}} \right)^2} - m - 1 > 0\)
⇔ m2 + 4m + 4 + m2 + 8m + 16 – 4m – 4 > 0
⇔ 2m2 + 8m + 16 > 0, ∀m ∈ ℝ.
Khi đó (Cm) luôn là đường tròn, với mọi giá trị của m.
Đường tròn (Cm) có tâm I có tọa độ là \(\left\{ \begin{array}{l}x = - \frac{{m + 2}}{2}\\y = \frac{{m + 4}}{2}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2x = - m - 2\,\,\,\,\left( 1 \right)\\2y = m + 4\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Lấy (1) + (2) vế theo vế, ta được 2x + 2y = –m – 2 + m + 4
⇔ 2x + 2y – 2 = 0
⇔ x + y – 1 = 0.
Vậy khi m thay đổi, tâm của đường tròn (Cm) luôn nằm trên đường thẳng có phương trình x + y – 1 = 0.
Do đó ta chọn phương án B.