Câu hỏi:
23/07/2024 8,723Cho đường tròn (C): x2 + y2 – 4x – 6y + 5 = 0. Đường thẳng d đi qua điểm A(3; 2) và cắt (C) theo một dây cung ngắn nhất có phương trình là:
A. 2x – y + 2 = 0;
B. x + y – 1 = 0;
C. x – y – 1 = 0;
D. x – y + 1 = 0.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
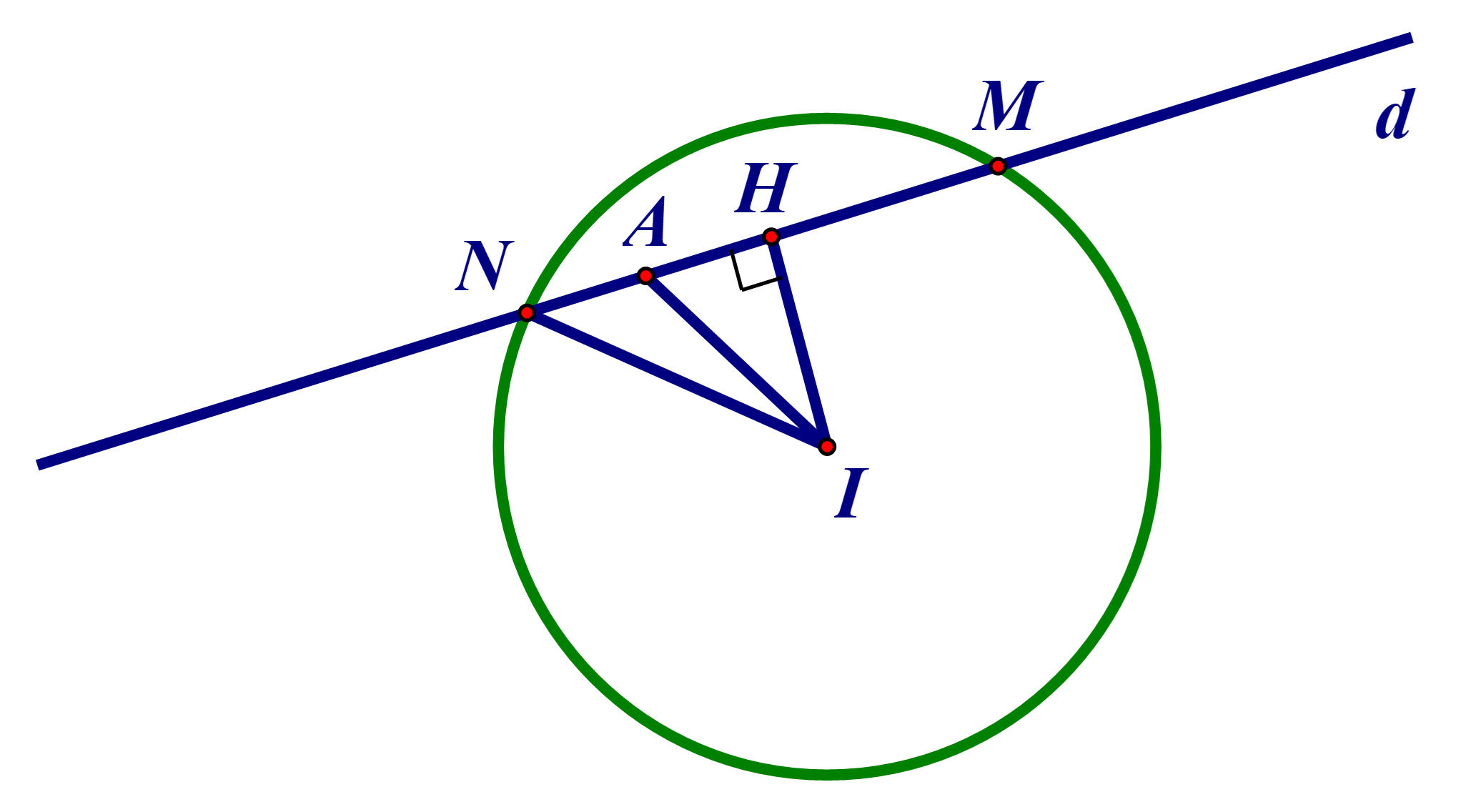
Đường tròn (C) có tâm I(2; 3), bán kính R=2√2.
Gọi M, N là giao điểm của đường thẳng d và đường tròn (C).
Kẻ IH ⊥ d. Suy ra H là trung điểm MN. Khi đó HN=12MN.
∆IHN vuông tại H: IN2 = IH2 + HN2 (Định lí Pytago)
⇔R2=IH2+(MN2)2
⇔(MN2)2=R2−IH2
Dây cung MN ngắn nhất khi và chỉ khi IH lớn nhất. Tức là IA ≡ IH hay A ≡ H.
Khi đó IA ⊥ d.
Suy ra d nhận →IA=(1;−1) làm vectơ pháp tuyến.
Đường thẳng d đi qua A(3; 2) và có vectơ pháp tuyến →IA=(1;−1).
Suy ra phương trình d: 1(x – 3) – 1(y – 2) = 0
⇔ x – y – 1 = 0.
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là: C

Đường tròn (C) có tâm I(2; 3), bán kính R=2√2.
Gọi M, N là giao điểm của đường thẳng d và đường tròn (C).
Kẻ IH ⊥ d. Suy ra H là trung điểm MN. Khi đó HN=12MN.
∆IHN vuông tại H: IN2 = IH2 + HN2 (Định lí Pytago)
⇔R2=IH2+(MN2)2
⇔(MN2)2=R2−IH2
Dây cung MN ngắn nhất khi và chỉ khi IH lớn nhất. Tức là IA ≡ IH hay A ≡ H.
Khi đó IA ⊥ d.
Suy ra d nhận →IA=(1;−1) làm vectơ pháp tuyến.
Đường thẳng d đi qua A(3; 2) và có vectơ pháp tuyến →IA=(1;−1).
Suy ra phương trình d: 1(x – 3) – 1(y – 2) = 0
⇔ x – y – 1 = 0.
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Đường tròn (C) đi qua hai điểm A(1; 3), B(3; 1) và có tâm nằm trên đường thẳng d: 2x – y + 7 = 0 có phương trình là:
Câu 2:
Cho đường tròn (C): x2 + y2 + 2x – 6y + 5 = 0. Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y – 15 = 0 là:
Câu 3:
Với giá trị nào của m thì đường thẳng ∆: 4x + 3y + m = 0 tiếp xúc với đường tròn (C): x2 + y2 – 9 = 0?


