Câu hỏi:
23/11/2024 12,886Đường tròn (C) đi qua hai điểm A(1; 3), B(3; 1) và có tâm nằm trên đường thẳng d: 2x – y + 7 = 0 có phương trình là:
A. (x – 7)2 + (y – 7)2 = 102;
B. (x + 7)2 + (y + 7)2 = 164;
C. (x – 3)2 + (y – 5)2 = 25;
D. (x + 3)2 + (y + 5)2 = 25.
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Lời giải
Gọi I(a; b) là tâm của đường tròn (C).
Ta có IA2 = IB2 = R2.
\( \Leftrightarrow {\left( {1 - a} \right)^2} + {\left( {3 - b} \right)^2} = {\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2}\)
⇔ 4a = 4b
⇔ a = b.
Khi đó tọa độ I(a; a).
Vì I(a; a) ∈ d nên 2a – a + 7 = 0
⇔ a = –7.
Suy ra I(–7; –7).
Ta có \(R = IA = \sqrt {{{\left( {1 + 7} \right)}^2} + {{\left( {3 + 7} \right)}^2}} = 2\sqrt {41} \).
Vậy phương trình đường tròn (C): (x + 7)2 + (y + 7)2 = 164.
*Phương pháp giải:
1.Gọi I là tâm dựa vào hàm số đè bài để tìm I
2.Suy ra r và viết phương trình đường tròn
*Lý thuyết:
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
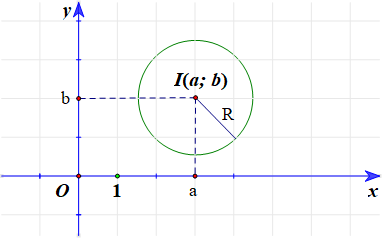Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạoCÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho đường tròn (C): x2 + y2 – 4x – 6y + 5 = 0. Đường thẳng d đi qua điểm A(3; 2) và cắt (C) theo một dây cung ngắn nhất có phương trình là:
Câu 2:
Cho đường tròn (C): x2 + y2 + 2x – 6y + 5 = 0. Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y – 15 = 0 là:
Câu 3:
Với giá trị nào của m thì đường thẳng ∆: 4x + 3y + m = 0 tiếp xúc với đường tròn (C): x2 + y2 – 9 = 0?
