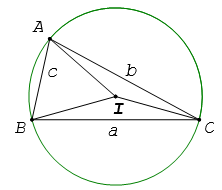
Trắc nghiệm Toán 10 Bài 2. Định lí côsin và định lí sin có đáp án
Trắc nghiệm Toán 10 Bài 2. Định lí côsin và định lí sin có đáp án
-
6144 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Tam giác ABC có BC=5√5,AC=5√2,AB=5. Số đo góc ˆA là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
cosA=AB2+AC2−BC22.AB.AC=52+(5√2)2−(5√5)22.5.5√2=−√22
⇒ˆA=135°
Vậy
Câu 2:
16/07/2024Tam giác ABC có , AC = 10. Độ dài cạnh AB là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác ABC có ta có:
(định lí tổng ba góc trong tam giác)
Áp dụng định lí sin trong tam giác ABC ta có:
Vậy
Câu 3:
22/07/2024Tam giác ABC có AB = 3, BC = 6. Số đo góc B là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
Câu 4:
10/11/2024Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải
Trong tam giác ABC có là góc tù nên là góc nhọn.
Áp dụng định lí sin trong tam giác ABC ta có:
(vì là góc nhọn)
Xét tam giác ABC có ta có:
(định lí tổng ba góc trong tam giác)
Vậy
*Phương pháp giải:
Sử dụng định lí Sin trong tam giác
tính góc B, C. Chú ý điều kiện B là góc tù.
Tính góc A = 1800 – (B + C).
*Lý thuyết:
Định lí sin:
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
Trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.
Từ định lí sin, ta có hệ quả sau đây:
Hệ quả:
a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;
Xem thêm
Tất tần tật về Định lí Sin (2024) chi tiết nhất
Lý thuyết Định lí côsin và định lí sin – Toán 10 Chân trời sáng tạo
Câu 5:
03/12/2024Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải:
Góc nhỏ nhất ứng với cạnh đối diện có độ dài nhỏ nhất.
Giả sử tam giác ABC có AB = 2, AC = 3, BC = 4. Khi đó góc nhỏ nhất là góc C ứng với cạnh đối diện AB.
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
Vậy côsin của góc nhỏ nhất trong tam giác bằng
*Phương pháp giải:
- giả sử ba cạnh lần lượt tương ứng để tính cho dễ
- Áp dụng định lý cosin trong tam giác để tìm ra ra góc
* Các lý thuyết cần nắm về các công thức trong hệ thức lượng tam giác:
Định lí côsin
Cho tam giác ABC có BC = a, AC = b và AB = c. Ta có
a2 = b2 + c2 – 2bc.cosA;
b2 = c2 + a2 – 2ca.cosB;
c2 = a2 + b2 – 2ab.cosC.
Hệ quả
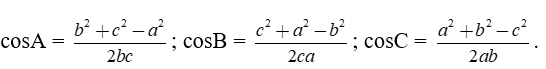
Định lí sin
Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.
Ta có
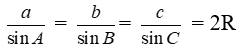
Xem thêm các bài viết liên quan hay, chi tiết:
Tất tần tật về Định lí Côsin và hệ quả chi tiết nhất
Giải Toán 10 Bài 2 (Chân trời sáng tạo): Định lí côsin và định lí sin
Trắc nghiệm Định lí côsin và định lí sin (Chân trời sáng tạo) có đáp án - Toán 10
Câu 6:
23/07/2024Diện tích của tam giác ABC với AB = 20, AC = 10 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Diện tích tam giác ABC là:
(đơn vị diện tích).
Vậy (đơn vị diện tích).Câu 7:
23/07/2024Diện tích tam giác có ba cạnh lần lượt là và 1 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Nửa chu vi tam giác có độ dài ba cạnh , 1 là:
Diện tích tam giác theo công thức Heron là:
Vậy
Câu 8:
22/07/2024Nếu tam giác ABC có BC2 < AB2 + AC2 thì:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:
Nếu BC2 < AB2 + AC2 thì AB2 + AC2 ‒ BC2 > 0
Do đó hay cosA > 0
Mà
Þ Góc là góc nhọn.
Câu 9:
22/07/2024Tam giác ABC có và BC = a. Tính bán kính đường tròn ngoại tiếp tam giác.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Xét tam giác ABC có ta có:
(định lí tổng ba góc trong tam giác)
Áp dụng định lí sin trong tam giác ABC ta có:
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là:
Câu 10:
23/07/2024Tam giác ABC có AB = 10, AC = 24, diện tích bằng 120. Độ dài đường trung tuyến AM là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Diện tích tam giác ABC là:
Mà
Þ DABC vuông tại A
Xét tam giác ABC vuông tại A, theo định lí Py – ta – go ta có:
BC2 = AB2 + AC2 Þ BC2 = 102 + 242 = 676
Þ BC = 26.
Do đó trung tuyến AM ứng với cạnh huyền BC có độ dài là:
Vậy độ dài đường trung tuyến AM bằng 13.
Câu 11:
20/07/2024Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Diện tích tam giác GEC là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
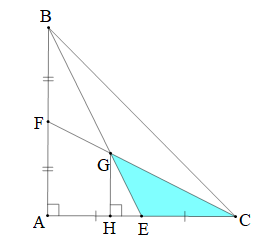
Vì BE là trung tuyến của tam giác ABC nên E là trung điểm của AC.
Do đó
Hai đường trung tuyến BE và CF cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Khi đó (tính chất trọng tâm của tam giác)
Hay
Gọi H là chân đường vuông góc kẻ từ G xuống AC.
Suy ra GH // AB.
Do đó (định lí Ta – let trong tam giác ABE)
Hay
Diện tích tam giác GEC là:
Vậy diện tích tam giác GEC là 75 cm2.
Câu 12:
19/07/2024Bán kính đường tròn nội tiếp tam giác có ba cạnh lần lượt là 5, 12, 13 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét tam giác có độ dài ba cạnh là 5, 12, 13 ta có: 52 + 122 = 169 và 132 = 169.
Do đó 52 + 122 = 132 nên tam giác này là tam giác vuông (định lí Py – ta – go đảo)
Diện tích tam giác này là: (đơn vị diện tích)
Nửa chu vi tam giác này là:
Mặt khác S = pr
Vậy bán kính đường tròn nội tiếp tam giác bằng 2.
Câu 13:
18/07/2024Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có diện tích ban đầu của tam giác ABC là: .
Diện tích của tam giác mới sau khi thay đổi kích thước là:
.
Vậy diện tích của tam giác mới được tạo thành là 6S.
Câu 14:
19/07/2024Hình bình hành có một cạnh là 4, hai đường chéo là 6 và 8. Độ dài cạnh kề với cạnh có độ dài bằng 4 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là B:
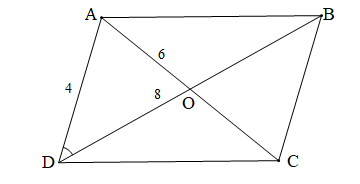
Hình bình hành có một cạnh là 4, hai đường chéo là 6 và 8 được mô tả như hình vẽ, do đó AD = 4, AC = 6, BD = 8.
Gọi O là giao điểm của hai đường chéo.
Khi đó O là trung điểm của AC và BD (tính chất hình bình hành).
Þ AO = 3 và DO = 4.
Áp dụng hệ quả định lí côsin vào tam giác ADO ta có:
Áp dụng định lí côsin vào tam giác ABD ta có:
AB2 = AD2 + BD2 – 2.AD.BD.
Þ AB2 = 42 + 82 – 2.4.8. = 34
Vậy độ dài cạnh kề với cạnh có độ dài bằng 4 của hình bình hành đó là
Câu 15:
24/11/2024Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Lời giải
Xét tam giác ABC vuông cân tại A, giả sử AB = AC = a, theo định lí Py – ta – go ta có:
BC2 = AB2 + AC2 = a2 + a2 = 2a2
Do đó nửa chu vi tam giác ABC là
Tam giác ABC vuông tại A nên diện tích tam giác ABC là:
(đơn vị diện tích)
Mặt khác
và
Do đó
Vậy
*Phương pháp giải:
Sử dụng công thức tính diệc tích tam giác để tính
*Lý thuyết:
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
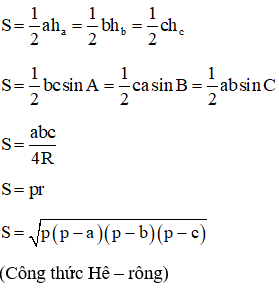
+ Phương pháp giải: Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
Xem thêm
Các công thức tính diện tích tam giác (2024) đầy đủ, chi tiết nhất
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 2. Định lí côsin và định lí sin có đáp án (6143 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 2. Định lí côsin và định lí sin có đáp án (Phần 2) (692 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 Bài 3. Giải tam giác và ứng dụng thực tế có đáp án (636 lượt thi)
- Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án (550 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án (Phần 2) (538 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài tập ôn tập chương 4 có đáp án (Phần 2) (496 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 3. Giải tam giác và ứng dụng thực tế có đáp án (Phần 2) (446 lượt thi)
- Trắc nghiệm Toán 10 Bài tập cuối chương 4 có đáp án (346 lượt thi)