Trắc nghiệm Tính chất ba đường trung tuyến trong tam giác (có đáp án)
Trắc nghiệm Toán 7 Bài 4: Tính chất ba đường trung tuyến trong tam giác
-
337 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
18/07/2024Cho tam giác ABC có G là trọng tâm tam giác, N là trung điểm AC. Khi đo BG = ... BN. Số thích hợp điền vào chỗ trống là:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
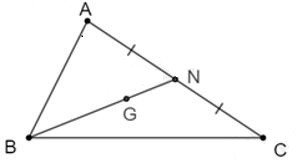
Vì G là trọng tâm của nên
Số thích hợp điền vào chỗ trống là
Câu 2:
21/07/2024Tam giác ABC có trung tuyến và G là trọng tâm. Độ dài đoạn AG là
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên
(tính chất ba đường trung tuyến của tam giác)
Do đó
Câu 3:
22/07/2024Điền số thích hợp vào chỗ chấm: "Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng ... độ dài đường trung tuyến đi qua đỉnh ấy"
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Định lý: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.
Số cần điền là
Câu 4:
18/07/2024Chọn câu sai
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
+ Một tam giác chỉ có một trọng tâm nên đáp án D sai.
Câu 5:
22/07/2024Cho hình vẽ sau
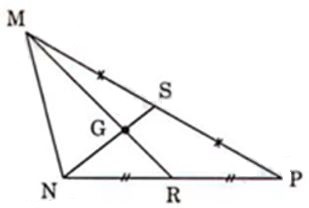
Biết MG = 3cm. Tính MR
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Ta có: MR, NS là hai đường trung tuyến của tam giác MNP và chúng cắt nhau tại G nên G là trọng tâm tam giác MNP
Theo tính chất ba đường trung tuyến của tam giác ta có:
Vậy MR = 4,5cm
Câu 6:
18/07/2024Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
- Đường trung tuyến của tam giác là đoạn thẳng nối đỉnh của tam giác với trung điểm của cạnh đối diện nên A đúng.
- Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó nên B, C đúng.
Câu 7:
21/07/2024Cho tam giác MNP, hai đường trung tuyến ME, NF cắt nhau tại O. Tính diện tích tam giác MNP, biết diện tích tam giác MNO là
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
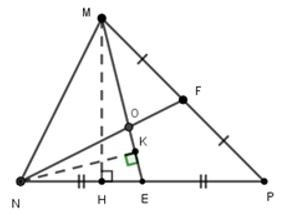
Gọi MH là đường cao kẻ từ M xuống cạnh BC, NK là đường cao kẻ từ N xuống cạnh ME.
Hai đường trung tuyến ME và NF cắt nhau tại O nên O là trọng tâm tam giác MNP, do đó
Có ME là trung tuyến ứng với cạnh NP nên E là trung điểm của NP, suy ra
Ta có:
Từ đó suy ra:
Câu 8:
18/07/2024Cho tam giác ABC có hai đường trung tuyến BD; CE sao cho . Khi đó tam giác ABC
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
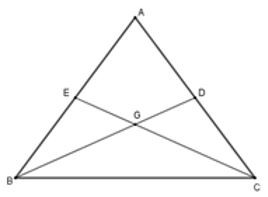
Hai đường trung tuyến BD và CE cắt nhau tại G suy ra G là trọng tâm tam giác ABC
Suy ra ; mà .
Từ đó:
Xét tam giác BGE và tam giác CGD có:
BG = CG
GD = GE
(đối đỉnh)
Do đó hay tam giác ABC cân tại A
Câu 9:
20/07/2024Tam giác ABC có trung tuyến và G là trọng tâm. Độ dài đoạn AG là
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Vì G là trọng tâm tam giác ABC và AM là đường trung tuyến nên
(tính chất ba đường trung tuyến của tam giác)
Do đó
Câu 10:
18/07/2024Cho tam giác ABC, có G là trọng tâm và các đường trung tuyến AM, BN, CP. Trên tia AG kéo dài lấy điểm D sao cho G là trung điểm của AD. So sánh các cạnh của tam giác BGD với các đường trung tuyến của tam giác ABC
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
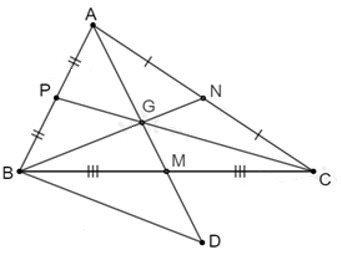
có G là trọng tâm và các đường trung tuyến AM, BN, CP nên theo tính chất ba đường trung tuyến của tam giác ta có:
Vì G là trung điểm của AD nên mà (cmt), do đó
Ta có: (tính chất ba đường trung tuyến của tam giác)
Mà
Xét và có:
GM = MD
(hai góc đối đỉnh)
BM = MC (vì AM là đường trung tuyến của )
(hai cạnh tương ứng) mà (cmt) nên (cmt)
Vậy
Câu 11:
18/07/2024Cho tam giác ABC vuông tại A có ; . Ba đường trung tuyến AM, BN, CE cắt nhau tại O. Độ dài trung tuyến CE là
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
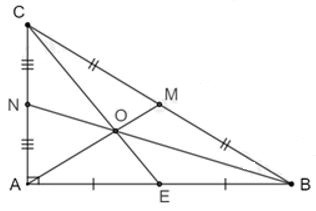
vuông tại A nên theo định lí Pytago ta có:
Ta có AM, BN, CE là các đường trung tuyến ứng với các cạnh BC, AC, AB của tam giác vuông ABC
Suy ra M, N, E lần lượt là trung điểm của các cạnh BC, AC, AB
Áp dụng định lí Pytago vào tam giác ACE vuông tại A ta có:
Câu 12:
23/07/2024Cho tam giác ABC có hai đường trung tuyến BD và CE vuông góc với nhau. Tính độ dài cạnh BC biết ;
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
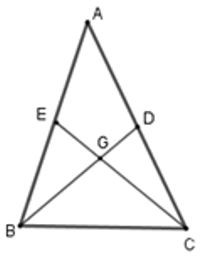
Gọi giao điểm của hai đường trung tuyến BD và CE là G thì G là trọng tâm tam giác ABC
Theo tính chất đường trung tuyến của tam giác ta có:
Mà ;
;
Xét tam goác BGC vuông tại G, theo định lí Pytago ta có:
Hay BC = 10cm
Vậy BC = 10cm
Câu 13:
18/07/2024Cho tam giác ABC, đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho . Gọi M, N theo thứ tự là trung điểm của BC; CE. Gọi I; K theo thứ tự là giao điểm của AM, AN và BE. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
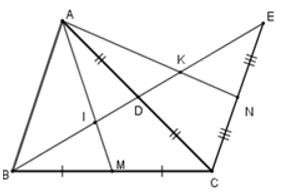
Vì AM, DB là hai đường trung tuyến của tam giác ABC và chúng cắt nhau tại I nên I là trọng tâm tam giác ABC
Khi đó: (1)
Vì AN, ED là hai đường trung tuyến của tam giác ACE và chúng cắt nhau tại K nên K là trọng tâm tam giác ACE nên
(2)
Từ (1) và (2) suy ra từ đó
Câu 14:
22/07/2024Cho tam giác ABC vuông tại A có: ; . Ba đường trung tuyến AM, BN, CE cắt nhau tại O
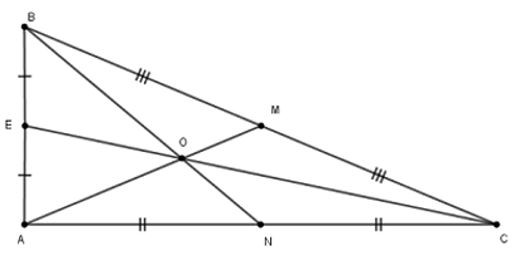
Độ dài trung tuyến BN là:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
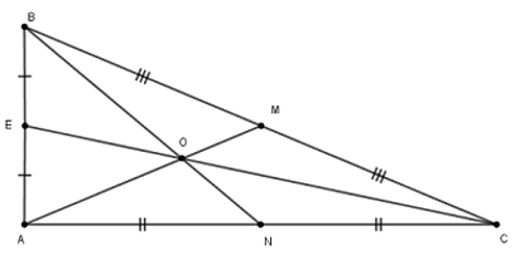
vuông tại A nên theo định lí Pytago ta có:
Ta có AM, BN, CE là các đường trung tuyến ứng với các cạnh BC, AC, AB của tam giác vuông ABC
Suy ra M, N, E lần lượt là trung điểm của các cạnh BC, AC, AB
Áp dụng định lí Pytago vào tam giác ABN vuông tại A ta có:
Câu 15:
20/07/2024Cho tam giác ABC có hai đường trung tuyến BD và CE vuông góc với nhau. Tính độ dài cạnh BC biết ;
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
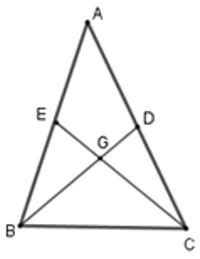
Gọi giao điểm của hai đường trung tuyến BD và CE là G thì G là trọng tâm tam giác ABC
Theo tính chất đường trung tuyến của tam giác ta có:
Mà ;
;
Xét tam goác BGC vuông tại G, theo định lí Pytago ta có:
Hay BC = 5cm
Vậy BC = 5cm
Câu 16:
22/07/2024Cho G là trọng tâm của tam giác đều. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
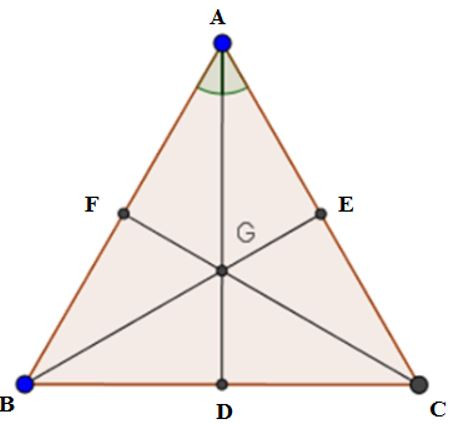
Các tia AG, BG và CG cắt BC, AC, AB lần lượt tại D, E, F thì D, E, F theo thứ tự lần lượt là trung điểm của BC, AC, AB
Mà (do tam giác ABC là tam giác đều), do đó
Xét và ta có:
AB = AC
chung
AE = AF
(1)
Chứng minh tương tự ta có:
(2)
Từ (1) và (2) ta có: (3)
Theo đề bài G là trọng tâm của tam giác ABC nên ta có:
; ;
Vì thế từ (3) ta suy ra
Câu 17:
18/07/2024Cho tam giác ABC, đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho . Gọi M, N theo thứ tự là trung điểm của BC; CE. Gọi I; K theo thứ tự là giao điểm của AM, AN và BE. Tính BE biết
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
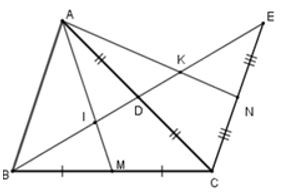
Ta có: mà
Vì AM, DB là hai đường trung tuyến của tam giác ABC và chúng cắt nhau tại I nên I là trọng tâm tam giác ABC
Khi đó: (1)
Vì AN, ED là hai đường trung tuyến của tam giác ACE và chúng cắt nhau tại K nên K là trọng tâm tam giác ACE nên
(2)
Mặt khác kết hợp với (1);(2) suy ra
Do đó:
Câu 18:
22/07/2024Tam giác ABC, các đường trung tuyến BD và CE. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
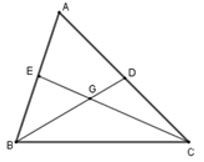
Gọi G là giao điểm của BD và CE. Trong ta có
Ta lại có: ; (tính chất các đường trung tuyến của tam giác ABC)
Từ đó:
Câu 19:
22/07/2024Cho G là trọng tâm của tam giác đều. D, E, F lần lượt là trung điểm của BC, AC, AB.Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
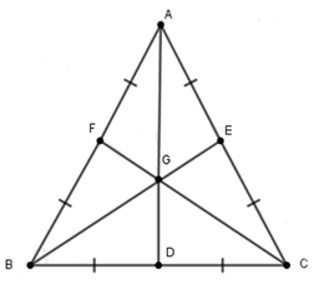
Vì D, E, F lần lượt là trung điểm của BC, AC, AB nên
Mặt khác (do tam giác ABC là tam giác đều), do đó
Xét và ta có:
AB = AC
chung
AE = AF
(1)
Chứng minh tương tự ta có
(2)
Từ (1) và (2) ta có: (3)
Theo đề bài G là trọng tâm của tam giác ABC nên ta có:
Kết hợp với (3) ta được:
Có thể bạn quan tâm
Các bài thi hot trong chương
- Trắc nghiệm Tính chất ba đường trung trực của tam giác (có đáp án) (518 lượt thi)
- Trắc nghiệm Tính chất đường trung trực của một đoạn thẳng (có đáp án) (356 lượt thi)
- Trắc nghiệm Tính chất ba đường cao của tam giác (có đáp án) (355 lượt thi)
- Trắc nghiệm Quan hệ giữa góc và cạnh đối diện trong tam giác (có đáp án) (351 lượt thi)
- Trắc nghiệm Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức trong tam giác (có đáp án) (347 lượt thi)
- Trắc nghiệm Tính chất ba đường phân giác của tam giác (có đáp án) (334 lượt thi)
- Trắc nghiệm Tính chất tia phân giác của một góc (có đáp án) (327 lượt thi)
- Trắc nghiệm Quan hệ giữa đường vuông góc và đường xiên. Đường xiên và hình chiếu của đường xiên (có đáp án) (311 lượt thi)
- Trắc nghiệm ôn tập chương 3 (có đáp án) (271 lượt thi)
