25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)

Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.

A. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 25$

B. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 4$

C. $(S) : {(x + 3)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 20$

D. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 5$

Xem đáp án

Câu 3:

19/07/2024

Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3) và đường thẳng d có phương trình $\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z + 3}{- 1}$ . Tính đường kính của mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d.

A. $5 \sqrt{2}$

B. $10 \sqrt{2}$

C. $2 \sqrt{5}$

D. $4 \sqrt{5}$

Xem đáp án

Câu 4:

Trong không gian Oxyz, cho điểm A(1;-2;3) và đường thẳng d có phương trình $\{\begin{matrix} x = - 1 + 2 t \\ y = 2 + t \\ z = - 3 - t \end{matrix} (t \in R)$ . Mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d có bán kính là:

A. $5 \sqrt{2}$

B. $10 \sqrt{2}$

C. $2 \sqrt{5}$

D. $4 \sqrt{5}$

Xem đáp án

Câu 5:

Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm $I (2; 0; 1)$ và tiếp xúc với đường thẳng $d : \frac{x - 1}{1} = \frac{y}{2} = \frac{z - 2}{1}$ là:

A. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 2$

B. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 9$

C. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 4$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 24$

Xem đáp án

Câu 6:

Lý thuyết Ôn tập chương 3 (mới 2024 + Bài Tập) – Toán 12

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $Δ$ có phương trình x=y=z. Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu không có hai điểm chung phân biệt với $Δ$ là:

A. $x^{2} + y^{2} + z^{2} + x + y + z - 6 = 0$

B. $x^{2} + y^{2} + z^{2} + 2 x - 4 y + 2 z - 3 = 0$

C. $x^{2} + y^{2} + z^{2} - 2 x + 3 y + 5 z + 3 = 0$

D. $x^{2} + y^{2} + z^{2} - 7 x - 2 z + 6 = 0$

Xem đáp án

Câu 7:

06/11/2024

Trong không gian Oxyz, cho đường thẳng

$d : \frac{x - 1}{1} = \frac{y + 1}{1} = \frac{z - m}{2}$ và mặt cầu $(S) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 9$ . Tìm m để đường thẳng d cắt mặt cầu (S) tại hai điểm phân biệt E, F sao cho độ dài đoạn thẳng EF lớn nhất.

A. m = 1

B. $m = - \frac{1}{3}$

C. m = 0

D. $m = \frac{1}{3}$

Xem đáp án

Đáp án đúng: C

*Lời giải:

*Phương pháp giải:

- từ phương trình mặt cầu: xác định tâm I(1,-1,m) và bán kính R

- đường thẳng (d) cắt mặt cầu (S) tại 2 điểm phân biệt E,F nên d(I,(d))min = EF min. Từ đó tìm ra điểm m

*Cách giải và các dạng bài toán về hệ trục tọa độ trong không gian:

Hệ tọa độ

Trong không gian, xét ba trục tọa độ x’Ox; y’Oy; z’Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi $\vec{i}; \vec{j}; \vec{k}$ lần lượt là các vectơ đơn vị, trên các trục x’Ox; y’Oy; z’Oz.

Hệ ba trục như vậy gọi là hệ trục tọa độ Đề- các vuông góc Oxyz trong không gian, hay đơn giản gọi là hệ trục tọa độ Oxyz. Điểm O được gọi là gốc tọa độ. Các mặt phẳng (Oxy); (Oyz); (Ozx) đôi một vuong góc với nhau được gọi là các mặt phẳng tọa độ. Không gian với hệ tọa độ Oxyz còn gọi là không gian Oxyz.

- Vì $\vec{i}; \vec{j}; \vec{k}$ là các vecto đơn vị đôi một vuông góc với nhau nên: ${\vec{i}}^{2} = {\vec{j}}^{2} = {\vec{k}}^{2} = 1$ và $\vec{i} . \vec{j} = \vec{j} . \vec{k} = \vec{k} . \vec{i} = 0$

Tọa độ của một điểm

- Trong không gian Oxyz, cho một điểm M tùy ý. Vì ba vecto $\vec{i}; \vec{j}; \vec{k}$ không đồng phẳng nên có một bộ ba số (x; y; z) duy nhất sao cho: $\vec{O M} = x . \vec{i} + y . \vec{j} + z . \vec{k}$

- Ngược lại, với bộ ba số (x; y; z) ta có một điểm M duy nhất trong không gian thỏa mãn hệ thức $\vec{O M} = x . \vec{i} + y . \vec{j} + z . \vec{k}$

- Ta gọi bộ ba số (x; y; z) là tọa độ của điểm M đối với hệ trục tọa độ Oxyz đã cho và viết: M = ( x; y; z) hoặc M (x; y; z).

Tọa độ của vecto

- Trong không gian Oxyz cho vecto $\vec{a}$ , khi đó luôn tồn tại duy nhất bộ ba số (a1; a2; a3) sao cho $\vec{a} = a_{1} . \vec{i} + a_{2} . \vec{j} + a_{3} . \vec{k}$

Ta gọi bộ ba số (a1; a2 ; a3) là tọa độ của vecto $\vec{a}$ đối với hệ tọa độ Oxyz cho trước và viết $\vec{a}$ (a1; a2 ; a3) hoặc $\vec{a}$ (a1; a2 ; a3).

- Nhận xét : Trong hệ tọa độ Oxyz, tọa độ của điểm M chính là tọa độ của vecto $\vec{O M}$

Ta có: M(x; y; z) $\Leftrightarrow \vec{O M} (x; y; z)$

Biểu thức tọa độ của các phép toán của vecto

- Định lí: Trong không gian Oxyz, cho hai vecto $\Leftrightarrow \vec{O M} (x; y; z)$

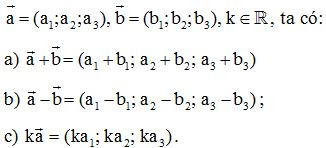
Biểu thức tọa độ của tích vô hướng.

Trong không gian Oxyz, tích vô hướng của hai vecto $\vec{a} = (a_{1}; a_{2}; a_{3}),$ $\vec{b} = (b_{1}; b_{2}; b_{3})$ được xác định bởi công thức: $\vec{a} . \vec{b} = a_{1} . b_{1} + a_{2} . b_{2} + a_{3} . b_{3}$

Ứng dụng

a) Độ dài của một vecto.

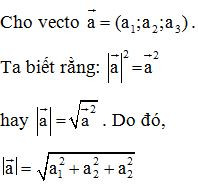
b) Khoảng cách giữa hai điểm.

Trong khong gian Oxyz, cho hai điểm A(xA ; yA ; zA) và B(xB; yB ; zB). Khi đó, khoảng cách giữa hai điểm A và B chính là độ dài của vecto $\vec{A B}$ . Do đó, ta có:

c) Góc giữa hai vecto.

Nếu là góc góc giữa hai vecto $\vec{a} = (a_{1}; a_{2}; a_{3})$ và $\vec{b} = (b_{1}; b_{2}; b_{3})$ với $\vec{a}; \vec{b} \neq \vec{0}$ thì

$\vec{a} . \vec{b} = a_{1} . b_{1} + a_{2} . b_{2} + a_{3} . b_{3}$

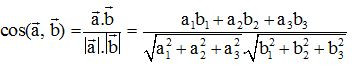
Từ đó, suy ra $\vec{a} ⊥ \vec{b} \Leftrightarrow$ $a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} = 0$ $\vec{a} . \vec{b} = a_{1} . b_{1} + a_{2} . b_{2} + a_{3} . b_{3}$

Xem thêm các bài viết liên quan hay, chi tiết

TOP 40 câu Trắc nghiệm Ôn tập Chương 3: Phương pháp tọa độ trong không gian (có đáp án 2024) - Toán 12

50 Bài tập Ôn tập Chương 3 Toán 12 mới nhất

Câu 8:

Trong bốn phương trình mặt cầu dưới đây, phương trình mặt cầu có điểm chung với trục Oz là:

A. $x^{2} + y^{2} + z^{2} + 4 x - 8 y + 2 z + 2 = 0$

B. $x^{2} + y^{2} + z^{2} + 2 x - 4 y - 2 z + 2 = 0$

C. $x^{2} + y^{2} + z^{2} + x - 2 y + z + 1 = 0$

D. $x^{2} + y^{2} + z^{2} - 2 x + 4 y + 4 z + 4 = 0$

Xem đáp án

Câu 9:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + {(y + 2)}^{2} + z^{2} = 5$ . Tìm tất cả các giá trị thực của tham số m để đường thẳng $Δ : \frac{x - 1}{2} = \frac{y + m}{1} = \frac{z - 2 m}{- 3}$ cắt (S) tại hai ddiemr phân biệt A, B sao cho A, B có độ dài AB lớn nhất

A. $m = - \frac{1}{2}$

B. $m = \pm \frac{1}{3}$

C. $m = \frac{1}{3}$

D. m = 0

Xem đáp án

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 50$ . Trong số các đường thẳng sau. Mặt cầu (S) tiếp xúc với đường nào.

A. $\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z + 3}{- 1}$

B. Trục Ox

C. Trục Oy

D. Trục Oz

Xem đáp án

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho điểm I(3;4;-2). Lập phương trình mặt cầu tâm I và tiếp xúc với trục Oz.

A. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 25$

B. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 4$

C. $(S) : {(x + 3)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 20$

D. $(S) : {(x - 3)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 5$

Xem đáp án

Câu 12:

14/07/2024

Xét đường thẳng d có phương trình $\{\begin{matrix} x = 1 + t \\ y = 2 \\ z = 3 + 2 t \end{matrix}$ và mặt cẩu (S) có phương trình ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 4$ . Nhận xét nào sau đây đúng.

A. d cắt (S) tại hai điểm phân biệt A, B và AB < 2R.

B. d không có điểm chung với (S)

C. d tiếp xúc với (S)

D. D cắt (S) tại hai điểm phân biệt A, B và AB đạt GTNN

Xem đáp án

Câu 13:

Có bao nhiêu mặt cầu (S) có tâm thuộc đường thẳng $Δ : \frac{x - 3}{2} = \frac{y - 1}{- 1} = \frac{z - 1}{- 2}$ đồng thời tiếp xúc với hai mặt phẳng $(α_{1}) : 2 x + 2 y + z - 6 = 0$ và $(α_{2}) : x - 2 y + 2 z = 0$

A. 1

B. 0

C. Vô số

D. 2

Xem đáp án

Câu 14:

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 9$ và đường thẳng $d : x - 1 = \frac{y - 2}{2} = \frac{z - 4}{3}$ . (d) cắt (S) tại hai điểm phân biệt A và B. Khi đó AB bằng:

A. $A B = \frac{\sqrt{126}}{7}$

B. $A B = \frac{\sqrt{123}}{7}$

C. $A B = \sqrt{\frac{126}{7}}$

D. $A B = \sqrt{\frac{129}{7}}$

Xem đáp án

Câu 15:

Trong không gian với hệ tọa độ Oxyz, phương trình mặt cầu (S) có tâm I(3;-2;0) và cắt trục Oy tại hai điểm A, B mà AB = 8 là:

A. ${(x - 3)}^{2} + {(y + 2)}^{2} + z^{2} = 9$

B. ${(x + 3)}^{2} + {(y - 2)}^{2} + z^{2} = 25$

C. ${(x - 3)}^{2} + {(y + 2)}^{2} + z^{2} = 64$

D. ${(x - 3)}^{2} + {(y + 2)}^{2} + z^{2} = 25$

Xem đáp án

Câu 16:

Trong không gian Oxyz, cho mặt cầu $(S) : {(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 6$ tiếp xúc với hai mặt phẳng $(P) : x + y + 2 z + 5 = 0$ , $(Q) : 2 x - y + z - 5 = 0$ lần lượt tại các điểm A, B. Độ dài đoạn thẳng AB là:

A. $2 \sqrt{3}$

B. $\sqrt{3}$

C. $2 \sqrt{6}$

D. $3 \sqrt{2}$

Xem đáp án

Câu 17:

23/07/2024

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng $d : \{\begin{matrix} x = 2 t \\ y = t \\ z = 4 \end{matrix}$ và $d' : \{\begin{matrix} x = t' \\ y = 3 - t' \\ z = 0 \end{matrix}$ . Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của hai đường thẳng d và d’là:

A. ${(x - 2)}^{2} + y^{2} + z^{2} = 4$

B. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 2$

C. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$

D. ${(x + 2)}^{2} + {(y + 1)}^{2} + z^{2} = 4$

Xem đáp án

Câu 18:

Trong không gian Oxyz, mặt phẳng $(P) : 2 x + 6 y + z - 3 = 0$ cắt trục Oz và đường thẳng $d : \frac{x - 5}{1} = \frac{y}{2} = \frac{z - 6}{- 1}$ lần lượt tại A và B. Phương trình mặt cầu đường kính AB là:

A. ${(x + 2)}^{2} + {(y - 1)}^{2} + {(z + 5)}^{2} = 36$

B. ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 5)}^{2} = 9$

C. ${(x + 2)}^{2} + {(y - 1)}^{2} + {(z + 5)}^{2} = 9$

D. ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 5)}^{2} = 36$

Xem đáp án

Câu 19:

18/07/2024

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình ${(x + 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$ . Phương trình nào sau đây là phương trình của mặt cầu đối xứng với mặt cầu (S) qua trục Oz

A. ${(x - 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4$

B. ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 4$

C. ${(x + 1)}^{2} + {(y + 1)}^{2} + {(z - 2)}^{2} = 4$

D. ${(x + 1)}^{2} + {(y - 1)}^{2} + {(z + 2)}^{2} = 4$

Xem đáp án

Câu 20:

Trong không gian với hệ tọa độ Oxyz. Hãy viết phương trình mặt cầu (S) có tâm $I (2; 0; 1)$ và tiếp xúc với đường thẳng $d : \frac{x - 1}{1} = \frac{y}{2} = \frac{z - 2}{1}$

A. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 2$

B. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 9$

C. ${(x - 2)}^{2} + y^{2} + {(z - 1)}^{2} = 4$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 1)}^{2} = 24$

Xem đáp án

Câu 21:

21/07/2024

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d : \frac{x - 1}{- 1} = \frac{y - 2}{1} = \frac{z + 1}{2}$ , điểm $A (2; - 1; 1)$ . Gọi I là hình chiếu vuông góc của A lên d. Viết phương trình mặt cầu (C) có tâm I và đi qua A.

A. $x^{2} + {(y - 3)}^{2} + {(z - 1)}^{2} = 20$

B. $x^{2} + {(y + 1)}^{2} + {(z + 2)}^{2} = 5$

C. ${(x - 2)}^{2} + {(y - 1)}^{2} + {(z + 3)}^{2} = 20$

D. ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 14$

Xem đáp án

Câu 22:

23/07/2024

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 4 y + 4 z - 16 = 0$ và đường thẳng $d : \frac{x - 1}{1} = \frac{y + 3}{2} = \frac{z}{2}$ . Mặt phẳng nào trong các mặt phẳng sau chứa d và tiếp xúc với mặt cầu (S)

A. $(P) : 2 x - 2 y + z - 8 = 0$

B. $(P) : - 2 x + 11 y - 10 z - 105 = 0$

C. $(P) : 2 x - 11 y + 10 z - 35 = 0$

D. $(P) : - 2 x + 2 y - z + 11 = 0$

Xem đáp án

Câu 23:

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 6 x + 4 y - 2 z + 5 = 0$ . Phương trình mặt phẳng (Q) chứa trục Ox và cắt (S) theo giao tuyến là một đường tròn bán kính bằng 2 là:

A. $(Q) : 2 y + z = 0$

B. $(Q) : 2 y - z = 0$

C. $(Q) : y - 2 z = 0$

D. $(Q) : 2 y - z = 0$

Xem đáp án

Câu 24: