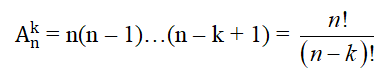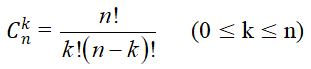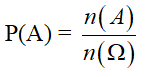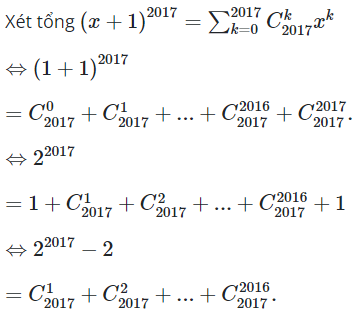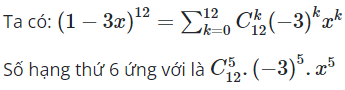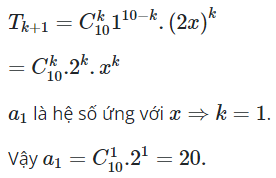Trắc nghiệm Toán 11 Ôn tập chương 2
-
627 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
23/07/2024Sắp xếp năm bạn học sinh An, Bình, Chi, Dũng, Lệ vào một chiếc ghế dài có 5 chỗ ngồi. Số cách sắp xếp sao cho bạn Chi luôn ngồi chính giữa là
 Xem đáp án
Xem đáp án
Chọn C.
Xếp bạn Chi luôn ngồi chính giữa: có 1 cách.
Xếp bốn bạn còn lại vào bốn vị trí còn lại: có 4!4! cách.
Vậy: có 1.4! = 24 cách.
Câu 3:
17/07/2024Một hộp chứa chín chiếc thẻ được đánh số từ 1 đến 9. Lấy ngẫu nhiên (đồng thời) hai thẻ. Số phần tử của không gian mẫu là
 Xem đáp án
Xem đáp án
Chọn C.
Lấy ngẫu nhiên (đồng thời) hai thẻ trong chín thẻ có: C29=36 cách.
Vậy số phần tử của không gian mẫu là C29=36
Câu 4:
18/07/2024Cho A={1;2;3;5;7}. Từ tập A có thể lập được bao nhiêu số tự nhiên gồm ba chữ số đôi một khác nhau?
 Xem đáp án
Xem đáp án
Chọn D.
Số các số tự nhiên gồm ba chữ số đôi một khác nhau được lập từ tập A là A35=60 số.
Vậy có: 60 số cần tìm.
Câu 5:
26/11/2024Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau?
 Xem đáp án
Xem đáp án
Đáp án đúng C.
*Lời giải:
Coi 4 nữ sinh là X .
Số cách sắp xếp X và nam sinh là 7!
Số cách sắp xếp 4 nữ sinh trong X là 4!
Số cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau: 7!.4! = 120960
*Phương pháp giải:
- Gộp 3 bạn nữ thành 1 phần tử lớn tìm số cách xếp cho 4 vị trí
- số cách xếp 3 bạn nam vào 3 vị tí
*Lý thuyết
-
Định nghĩa
Cho tập hợp A gồm n phần tử (n ∈ ℕ*).
Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.
1. Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m+n cách thực hiện.
2. Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.
3. Hoán vị:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử.
- Số các hoán vị của n phần tử là: Pn = n(n-1)...2.1 = n!
4. Chỉnh hợp:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
- Số các chỉnh hợp chập k của n phần tử là:
5. Tổ hợp:
Giả sử A có n phần tử (n ≥ 1).
- Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).
Số các tổ hợp chập k của n phần tử là:
6. Công thức nhị thức Niu-tơn:
(a + b)n = Cn0an + Cn1an - 1b + … + Cnkan - kbk + … + Cnn-1abn-1 + Cnnbn
7. Phép toán trên các biến cố:
- Giả sử A là biến cố liên quan đến một phép thử.
Khi đó, tập Ω\A được gọi là biến cố đối của biến cố A, kí hiệu là A−.
- Giả sử A và B là hai biến cố liên quan đến một phép thử:
+ Tập A ⋃ B được gọi là hợp của các biến cố A và B.
+ Tập A ⋂ B được gọi là giao của các biến cố A và B.
+ Nếu A ⋂ B = ∅ thì ta nói A và B xung khắc.
8. Xác suất của biến cố:
Giả sử A là biến cố liên quan đến phép thử chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, xác suất của biến cố A là:
trong đó: n(A) là số phần tử của A; còn n(Ω) là số các kết quả có thể xảy ra của phép thử.
9. Tính chất của xác suất:
Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện.
P(∅) = 0, P(Ω) = 1
0 ≤ P(A) ≤ 1, với mọi biến cố A.
Nếu A và B xung khắc, thì P(AB) = P(A) + P(B) (công thức cộng xác suất)
Với mọi biến cố A, ta có: P(A−) = 1 – P(A).
A và B là hai biến cố độc lập khi và chỉ khi P(A.B) = P(A).P(B).
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Tổ hợp - xác suất hay, chi tiết
Câu 6:
20/07/2024Từ một hộp đựng 30 thẻ được đánh số từ 1 đến 30, rút ngẫu nhiên 10 thẻ. Gọi A là biến cố rút được 5 thẻ đánh số lẻ, 5 thẻ đánh số chẵn và có đúng hai thẻ có số chia hết cho 10. Tìm số phần tử của A .
 Xem đáp án
Xem đáp án
Chọn C.
Chọn 3 thẻ chia hết cho 10 từ các số {10;20;30} có C23C23 cách chọn.
Chọn 3 thẻ chẵn nhưng không chia hết cho 10 có C312 cách chọn.
Chọn 5 thẻ lẻ có C515
Suy ra có 3.C312.C515 cách chọn số phần tử của A .
Câu 7:
23/07/2024Cho hai đường thẳng song song d1, . Trên lấy 5 điểm phân biệt tô màu xanh, trên lấy 8 điểm phân biệt tô màu đỏ. Xét tất cả các tam giác có đỉnh lấy từ các điểm trên. Chọn ngẫu nhiên một tam giác. Tính xác suất để tam giác được chọn có đúng hai đỉnh màu xanh.
 Xem đáp án
Xem đáp án
Chọn D.
Số cách chọn tam giác có đỉnh lấy từ các điểm trên là
A: Biến cố tam giác được chọn có đúng hai đỉnh màu xanh
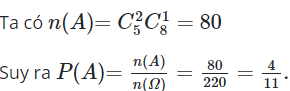
Câu 8:
20/07/2024Đội học sinh giỏi cấp trường môn Tiếng Anh của trường THPT chuyên Vĩnh Phúc gồm 8 học sinh khối 10, 8 học sinh khối 11 và 8 học sinh khối 12. Nhà trường cần chọn 10 học sinh tham gia câu lạc bộ tiếng Anh của trường. Tính số cách chọn sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10.
 Xem đáp án
Xem đáp án
Chọn B.
Chọn sao cho có học sinh cả ba khối và có nhiều nhất 2 học sinh khối 10 có các khả năng sau.
TH1: Có 1 học sinh khối 10.
Số cách chọn trong trường hợp này là
TH2: Có 2 học sinh khối 10.
Số cách chọn trong trường hợp này là
Vậy áp dụng quy tắc cộng ta có ![]()
Câu 9:
20/07/2024Có 3 xạ thủ bắn độc lập vào bia. Xác suất bắn trúng của mỗi xạ thủ lần lượt là 0,6; 0,8 và 0,9. Tính xác suất để trong 3 xạ thủ có đúng 2 xạ thủ bắn trúng bia.
 Xem đáp án
Xem đáp án
Chọn D.
Gọi với là các biến cố xạ thủ thứ i bắn trúng bia.
Theo giả thiết, ta có ![]()
Khi đó, xác suất để trong 3 xạ thủ có đúng 2 xạ thủ bắn trúng bia là
Câu 10:
23/07/2024Hệ số của trong khai triển là
 Xem đáp án
Xem đáp án
Chọn D.
Số hạng tổng quát của khai triển:
![]()
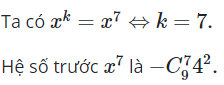
Câu 11:
17/07/2024Từ các chữ số 0 ; 1; 2 ; 3 ; 5 lập được bao nhiêu số gồm có 4 chữ số khác nhau và không chia hết cho 5 ?
 Xem đáp án
Xem đáp án
Chọn A.

Câu 12:
21/07/2024Giải bóng đá ngoại hạng Anh có 20 đội bóng tham gia thi đấu vòng tròn 2 lượt. Hỏi có bao nhiêu trận đấu sẽ được tổ chức?
 Xem đáp án
Xem đáp án
Chọn C.
Cứ hai đội gặp nhau cho ta một trận đấu nên số trận đấu một lượt là
Số trận đấu hai lượt là trận.
Câu 13:
21/07/2024Trong 1 hộp đựng 4 viên bi đỏ và 3 viên bi xanh, lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy ra 2 viên cùng màu?
 Xem đáp án
Xem đáp án
Chọn C.

Câu 16:
18/07/2024Trên giá sách của bạn Minh có 4 quyển truyện khác nhau và 6 quyển tạp chí khác nhau. Bạn Minh chọn một quyển truyện hoặc một quyển tạp chí để cho bạn Sáng mượn. Hỏi bạn Minh có bao nhiêu cách chọn.
 Xem đáp án
Xem đáp án
Chọn B.
Số cách bạn Minh chọn một quyển truyện cho bạn Sáng mượn là 4 cách.
Số cách bạn Minh chọn một quyển tạp chí cho bạn Sáng mượn là 6 cách.
Vậy bạn Minh có 4+6=10 cách chọn một quyển truyện hoặc một quyển tạp chí để cho bạn Sáng mượn.
Câu 17:
23/07/2024Có bao nhiêu cách sắp xếp năm bạn An, Bình, Châu, Dung và Đức đứng thành một hàng ngang?
 Xem đáp án
Xem đáp án
Chọn C.
Số cách sắp xếp năm bạn thành một hàng ngang là các hoán vị của năm phần tử có 5! = 120 cách.
Câu 18:
20/07/2024Cho tập hợp M có 12 phần tử. Số tập con gồm 3 phần tử của M là
 Xem đáp án
Xem đáp án
Chọn B.
Số tập con gồm 3 phần tử của M là số cách chọn 3 phần tử không phân biệt thứ tự từ 12 phần tử.
Vậy có tập hợp.
Câu 21:
17/11/2024Số cách sắp xếp 4 nam sinh và 3 nữ sinh vào một dãy ghế hàng ngang có 7 chỗ ngồi là
 Xem đáp án
Xem đáp án
Đáp án đúng là A.
Lời giải
Số cách sắp xếp 7 học sinh vào dãy ghế hang ngang có 7!
*Phương pháp giải:
Sử dụng lý thuyết hoán vị P=n!
*Lý thuyết:
1. Định nghĩa
Cho tập hợp A gồm n phần tử (n ∈ ℕ*).
Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.
Ví dụ: Từ 3 chữ số 3, 5, 7 có thể lập được bao nhiêu số có ba chữ số khác nhau ?
Hướng dẫn giải
Mỗi cách sắp xếp ba chữ số đã cho để lập thành một số có ba chữ số khác nhau là một hoán vị của ba chữ số đó.
Ta có các số sau : 357 ; 375 ; 537 ; 573 ; 735 ; 753.
Vậy có 6 số có ba chữ số khác nhau lập từ ba chữ số 3, 5, 7.
2. Số các hoán vị
Kí hiệu Pn là số các hoán vị của n phần tử. Ta có Pn = n . (n – 1) … 2.1
Quy ước : Tích 1.2…n được viết là n! (đọc là n giai thừa), tức là n! = 1 . 2 … n.
Như vậy Pn = n!.
Ví dụ: Có ba bạn học sinh Nam, Long, Vinh. Giáo viên muốn xếp ba bạn này vào 3 vị trí chỗ ngồi. Hỏi có bao nhiêu cách xếp.
Hướng dẫn giải
Xếp ba bạn Nam, Long, Vinh vào 3 vị trí chỗ ngồi là một hoán vị của 3 bạn.
Ta có P3 = 3! = 1.2.3 = 6.
Vậy có 6 cách xếp 3 bạn Nam, Long, Vinh vào ba vị trí chỗ ngồi.
Xem thêm
Câu 23:
20/11/2024Một hộp chứa 6 viên bi gồm 3 viên bi xanh, 2 viên bi vàng và 1 viên bi trắng. Lấy ngẫu nhiên 3 viên bi từ hộp đó. Tính xác suất để lấy được ba viên bi có đủ ba màu.
 Xem đáp án
Xem đáp án
Đáp án đúng là D.
Lời giải
Số phần tử không gian mẫu
Gọi A là biến cố lấy được ba viên bi có đủ ba màu.
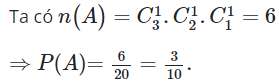
*Phương pháp giải:
Bước 1: Liệt kê kết quả có thể xảy ra và viết không gian mẫu Ω.
Bước 2: Đếm số kết quả thuận lợi cho biến cố.
Bước 3: Tính xác suất
*Lý thuyết:
Một tổ hợp chập k của n là một cách chọn k phần tử từ một tập hợp n phần tử (với k, n là các số tự nhiên, 0 ≤ k ≤ n).
Số các tổ hợp chập k của n, kí hiệu là , được tính bằng công thức :
Chú ý :
+) <
+) Chỉnh hợp và tổ hợp có điểm giống nhau là đều chọn một số phần tử trong một tập hợp, nhưng khác nhau ở chỗ, chỉnh hợp là chọn có xếp thứ tự, còn tổ hợp là chọn không xếp thứ tự.
Ví dụ : Một tổ có 10 người, bạn tổ trưởng muốn cử ra 5 bạn đi trực nhật. Hỏi có bao nhiêu cách chọn ?
Hướng dẫn giải
Mỗi cách chọn lần lượt 5 bạn trong 10 bạn đi trực nhật là một tổ hợp chập 5 của 10.
Ta có
Vậy có 252 cách chọn 5 trong 10 bạn đi trực nhật.
Sử dụng công thức xác suất cổ điển
Cho phép thử T có không gian mẫu là Ω. Giả thiết rằng các kết quả có thể của T là đồng khả năng. Khi đó nếu E là một biến cố liên quan đến phép thử T thì xác suất của E được cho bởi công thức.
P(E) = , trong đó n(Ω) và n(E) tương ứng là số phần tử của tập Ω và tập E.
Xem thêm
Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - Toán 10 Kết nối tri thức
Câu 24:
18/07/2024Gieo hai con súc sắc cân đối đồng chất. Tính xác suất để hiệu số chấm xuất hiện của hai con súc sắc bằng 1.
 Xem đáp án
Xem đáp án
Chọn C.
Số phần tử không gian mẫu
Gọi A là biến cố hiệu số chấm xuất hiện của hai con súc sắc bằng 1.
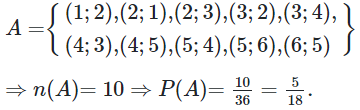
Câu 25:
23/07/2024Có ba chiếc hộp mỗi hộp đựng 2 viên bi xanh và 8 viên bi đỏ. Lấy ngẫu nhiên từ mỗi hộp một viên bi. Tính xác suất để trong 3 viên bi lấy được có ít nhất 1 viên bi xanh?
 Xem đáp án
Xem đáp án
Chọn B.
Gọi là không gian mẫu của phép thử.
Số cách lấy mỗi hộp một viên bi: (cách).
Suy ra, số phần tử của ![]()
Gọi A là biến cố: “Trong 3 viên bi lấy được có ít nhất 1 viên bi xanh”
Suy ra là biến cố: “Trong 3 viên bi lấy được không có viên bi xanh”
Số cách lấy mỗi hộp một viên bi sao cho không có bi xanh: 8.8.8 = 512 (cách).
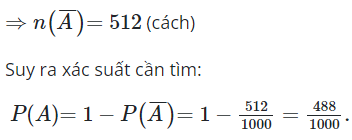
Câu 26:
23/07/2024Cho đa giác đều có 14 đỉnh. Chọn ngẫu nhiên 3 đỉnh trong 14 đỉnh của đa giác. Tính xác suất để 3 đỉnh được chọn là 3 đỉnh của một tam giác vuông.
 Xem đáp án
Xem đáp án
Chọn B.
Chọn ngẫu nhiên 3 đỉnh trong 14 đỉnh của đa giác
![]()
Gọi A là biến cố: "3 đỉnh được chọn là 3 đỉnh của tam giác vuông"
Chọn một đường chéo đi qua tâm, có 7 cách chọn.
Tương ứng với mỗi đường kính ấy, mỗi đỉnh còn lại sẽ tạo với đường kính một tam giác vuông. Khi đó, số tam giác vuông được tạo ra là
![]()
Vậy xác suất cần tính là ![]()
Câu 27:
19/11/2024Một tổ học sinh có 6 nam và 4 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ.
 Xem đáp án
Xem đáp án
Đáp án đúng là B.
Lời giải
Chọn 2 học sinh bất kì từ 10 học sinh có (cách chọn).
Chọn 2 học sinh nữ từ 4 học sinh nữ có (cách chọn).
Vậy xác suất cần tính là
*Phương pháp giải:
Tính không gian mẫu
Tính biến cố A
Tính xác suất
*Lý thuyết:
3. Tổ hợp
Một tổ hợp chập k của n là một cách chọn k phần tử từ một tập hợp n phần tử (với k, n là các số tự nhiên, 0 ≤ k ≤ n).
Số các tổ hợp chập k của n, kí hiệu là , được tính bằng công thức :
Chú ý :
+) <
+) Chỉnh hợp và tổ hợp có điểm giống nhau là đều chọn một số phần tử trong một tập hợp, nhưng khác nhau ở chỗ, chỉnh hợp là chọn có xếp thứ tự, còn tổ hợp là chọn không xếp thứ tự.
Xem thêm
Lý thuyết Hoán vị, chỉnh hợp và tổ hợp - Toán 10 Kết nối tri thức
Câu 28:
19/07/2024Một bình đựng 8 viên bi xanh và 4 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi trong bình. Xác suất để có được ít nhất hai viên bi xanh là
 Xem đáp án
Xem đáp án
Chọn C.
Lấy ngẫu nhiên 3 viên bi trong bình thì số phần tử của không gian mẫu là
Gọi A là biến cố “được ít nhất hai viên bi xanh”.
Ta có số phần tử thuận lợi cho biến cố A là
Vậy xác suất của A là ![]()
Câu 29:
17/07/2024Một trường THPT có 4 học sinh giỏi toán là nam, 5 học sinh giỏi văn là nam và 3 học sinh giỏi văn là nữ. Cần chọn 3 em đi dự đại hội ở Tỉnh. Tính xác suất để trong 3 em được chọn có cả nam lẫn nữ, có cả học sinh giỏi toán và học sinh giỏi văn.
 Xem đáp án
Xem đáp án
Chọn C.
Chọn 3 trong tổng số 12 học sinh: ![]()
Trong 3 em được chọn có cả nam lẫn nữ, có cả học sinh giỏi toán và học sinh giỏi văn:
+ Chọn 1 toán nam, 2 văn nữ: ![]()
+ Chọn 1 toán nam, 1 văn nam, 1 văn nữ: ![]()
+ Chọn 2 toán nam, 1 văn nữ:
![]()
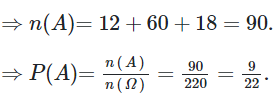
Câu 30:
20/07/2024Tìm hệ số lớn nhất trong khai triển biết tổng các hệ số bằng 4096.
 Xem đáp án
Xem đáp án
Chọn C.
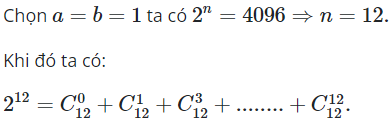
Hệ số của số hạng thứ 7 là hệ số lớn nhất bằng
Có thể bạn quan tâm
- Trắc nghiệm Ôn chương 2 (có đáp án) (626 lượt thi)
- 100 câu trắc nghiệm Tổ hợp - Xác suất cơ bản (P1) (2310 lượt thi)
- 100 câu trắc nghiệm Tổ hợp - Xác suất nâng cao (P1) (1769 lượt thi)
- Trắc nghiệm tổng hợp Chương 2 : Tổ hợp - Xác suất có đáp án (Phần 1) (769 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Nhị thức Niu-tơn (có đáp án) (1046 lượt thi)
- Trắc nghiệm Hoán vị - Chỉnh hợp - Tổ hợp (có đáp án) (1037 lượt thi)
- Trắc nghiệm Nhị thức Niu-tơn có đáp án (Thông hiểu) (926 lượt thi)
- Trắc nghiệm Hoán vị - Chỉnh hợp - Tổ hợp có đáp án (Thông hiểu) (893 lượt thi)
- Trắc nghiệm Quy tắc đếm có đáp án (Thông hiểu) (862 lượt thi)
- Trắc nghiệm Phép thử và biến cố (có đáp án) (834 lượt thi)
- Trắc nghiệm Quy tắc đếm (có đáp án) (814 lượt thi)
- Trắc nghiệm Xác suất của biến cố (có đáp án) (749 lượt thi)
- Trắc nghiệm Biến ngẫu nhiên rời rạc có đáp án (Nhận biết) (680 lượt thi)
- Trắc nghiệm Xác suất của biến cố có đáp án (Phần 2) (558 lượt thi)