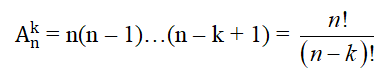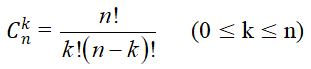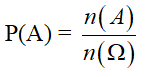Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau?

Đáp án đúng C.

*Lời giải:      

Coi 4 nữ sinh là X .

Số cách sắp xếp X và nam sinh là $\mathrm{7!}$

Số cách sắp xếp 4 nữ sinh trong X là $\mathrm{4!}$

Số cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau: $7!.4!\; =\; 120960$

$*Phương\; pháp\; giải:$

• Gộp 3 bạn nữ thành 1 phần tử lớn tìm số cách xếp cho 4 vị trí
• số cách xếp 3 bạn nam vào 3 vị tí

$*Lý\; thuyết$

• Định nghĩa

  Cho tập hợp A gồm n phần tử (n ∈ ℕ^*).

  Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.

  1. Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m+n cách thực hiện.

  2. Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.

  3. Hoán vị:

  Cho tập hợp A gồm n phần tử (n ≥ 1).

  - Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử.

  - Số các hoán vị của n phần tử là: Pn = n(n-1)...2.1 = n!

  4. Chỉnh hợp:

  Cho tập hợp A gồm n phần tử (n ≥ 1).

  - Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.

  - Số các chỉnh hợp chập k của n phần tử là:

  

  5. Tổ hợp:

  Giả sử A có n phần tử (n ≥ 1).

  - Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).

  Số các tổ hợp chập k của n phần tử là:

  

  6. Công thức nhị thức Niu-tơn:

      (a + b)n = Cn0an + Cn1an - 1b + … + Cnkan - kbk + … + Cnn-1abn-1 + Cnnbn

  7. Phép toán trên các biến cố:

  - Giả sử A là biến cố liên quan đến một phép thử.

  Khi đó, tập Ω\A được gọi là biến cố đối của biến cố A, kí hiệu là A−.

  - Giả sử A và B là hai biến cố liên quan đến một phép thử:

      + Tập A ⋃ B được gọi là hợp của các biến cố A và B.

      + Tập A ⋂ B được gọi là giao của các biến cố A và B.

      + Nếu A ⋂ B = ∅ thì ta nói A và B xung khắc.

  8. Xác suất của biến cố:

  Giả sử A là biến cố liên quan đến phép thử chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, xác suất của biến cố A là: 

  trong đó: n(A) là số phần tử của A; còn n(Ω) là số các kết quả có thể xảy ra của phép thử.

  9. Tính chất của xác suất:

  Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện.

      P(∅) = 0, P(Ω) = 1

      0 ≤ P(A) ≤ 1, với mọi biến cố A.

      Nếu A và B xung khắc, thì P(AB) = P(A) + P(B) (công thức cộng xác suất)

      Với mọi biến cố A, ta có: P(A−) = 1 – P(A).

      A và B là hai biến cố độc lập khi và chỉ khi P(A.B) = P(A).P(B).

  Xem thêm các bài viết liên quan hay, chi tiết

  Lý thuyết Tổ hợp - xác suất hay, chi tiết 

  Giải Toán 11 Chương 2: Tổ hợp – xác suất 

  Các dạng bài tập Tổ hợp - Xác suất