Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (Vận dụng)
Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (Vận dụng)
-
385 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 3:
23/11/2024Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB và CD. Mặt phẳng qua MN cắt AD,BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?
Xem đáp án
Đáp án đúng: B
* Lời giải:
* Phương pháp giải:
- Nắm kỹ lại lý thuyết và hai đường thẳng chéo nhau
*Một số lý thuyết và dạng bài tập về hai đường thẳng chéo nhau và hai đường thẳng song song:
Vị trí tương đối của hai đường thẳng trong không gian.
Cho hai đường thẳng a và b trong không gian. Khi đó có thể xảy ra một trong các trường hợp sau:
- Trường hợp 1. Có một mặt phẳng chứa a và b.
Khi đó, ta nói a và b đồng phẳng. Theo kết quả của hình học phẳng có 3 khả năng xảy ra:
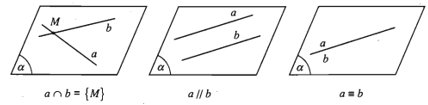
i) a và b có điểm chung duy nhất M. Ta nói a và b cắt nhau tại M và kí hiệu . Ta có thể viết .
ii) a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b.
iii) a trùng b, kí hiệu là .
- Trường hợp 2. Không có mặt phẳng nào chứa a và b.
Khi đó ta nói a và b chéo nhau hay a chéo với b.
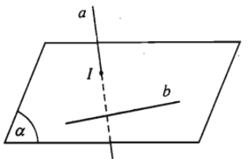
Tính chất
- Định lí. Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
- Định lí (về giao tuyến của ba mặt phẳng).
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
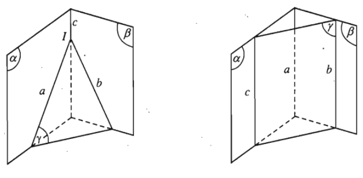
- Hệ quả. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hai đường thẳng chéo nhau và hai đường thẳng song song
Toán 11 Bài 2 giải vở bài tập: Hai đường thẳng chéo nhau và hai đường thẳng song song
Câu 7:
12/10/2024Cho tứ giác ABCD có AC và BD giao nhau tại O và một điểm S không thuộc mặt phẳng ABCD. Trên đoạn SC lấy một điểm M không trùng với S và C. Giao điểm của đường thẳng SD với mặt phẳng (ABM) là
Xem đáp án
*Phương pháp giải:
Muốn tìm giao điểm của đường thẳng d và mặt phẳng (P), có hai cách làm như sau:
* Cách 1:
+ Những bài đơn giản, có sẵn một mặt phẳng (Q) chứa đường thẳng d và một đường thẳng a nào đó thuộc mặt phẳng (P)
+ Trong mp( Q), 2 đường thẳng a và d cắt nhau tai điểm A. Khi đó điểm A chính là giao điểm của đường thẳng d và mp(P)
* Cách 2: Chọn mặt phẳng phụ:
+ Tìm một mặt phẳng (Q) chứa đường thẳng d, sao cho dễ dàng tìm giao tuyến của mp (Q) với mp (P)
+ Tìm giao tuyến của mp(P) và (Q) - gọi là đường thẳng d.
+ Tìm giao điểm của đường thẳng a và đường thẳng d - gọi là điểm A
Khi đó: điểm A chính là giao điểm của đường thẳng d và mp (P)
*Lời giải:
* Một số lý thuyết liên quan:
- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
- Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.
- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu hoặc .
- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu .
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.
Xem thêm các bài viết liên quan hay, chi tiết:
100 câu trắc nghiệm Đường thẳng, Mặt phẳng trong không gian nâng cao (phần 1)
50 bài tập Đại cương về đường thẳng (có đáp án 2024) và cách giải
Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Vận dụng)
