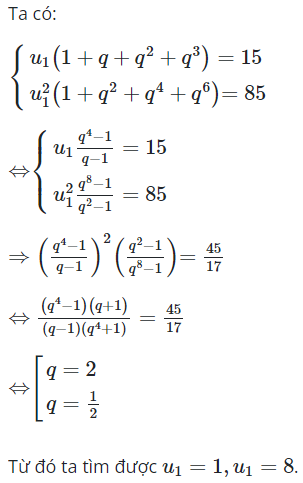30 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 11 Bài 4: Cấp số nhân

Tìm x biết : $1, x^{2}, 6 - x^{2}$ lập thành cấp số nhân.

A. $x = \pm 1$

B. $x = \pm \sqrt{2}$

C. $x = \pm 2$

D. $x = \pm \sqrt{3}$

Xem đáp án

Chọn B.

Ta có: $1, x^{2}, 6 - x^{2}$ lập thành cấp số nhân

$\Leftrightarrow x^{4} = 6 - x^{2}$

$\Leftrightarrow x = \pm \sqrt{2}$

Câu 2:

Các số $x + 6 y, 5 x + 2 y, 8 x + y$ lập thành cấp số cộng và các số $x + \frac{5}{3} y, y - 1, 2 x - 3 y$ lập thành cấp số nhân.

A.

B.

C.

D.

Xem đáp án

Chọn A.

Ta có hệ: $\{\begin{cases} x + 6 y + 8 x + y = 2 (5 x + 2 y) \\ (x + \frac{5}{3} y) (2 x - 3 y) = {(y - 1)}^{2} \end{cases}$

giải hệ này ta tìm được $(x; y) = (- 3; - 1); (\frac{3}{8}; \frac{1}{8})$

Câu 3:

Cho cấp số nhân $(u_{n})$ có các số hạng khác không, tìm $u_{1}$ biết:

$\{\begin{cases} u_{1} + u_{2} + u_{3} + u_{4} + u_{5} = 11 \\ u_{1} + u_{5} = \frac{82}{11} \end{cases}$

A. $u_{1} = \frac{1}{11}, u_{1} = \frac{81}{11}$

B. $u_{1} = \frac{1}{12}, u_{1} = \frac{81}{12}$

C. $u_{1} = \frac{1}{13}, u_{1} = \frac{81}{13}$

D. $u_{1} = \frac{2}{11}, u_{1} = \frac{81}{11}$

Xem đáp án

Chọn A

Ta có:

$\{\begin{cases} u_{1} (1 + q + q^{2} + q^{3} + q^{4}) = 11 \\ u_{1} (1 + q^{4}) = \frac{82}{11} \end{cases}$

$\Leftrightarrow \{\begin{cases} u_{1} q (1 + q + q^{2}) = \frac{39}{11} \\ u_{1} (1 + q^{4}) = \frac{82}{11} \end{cases}$

$\Rightarrow \frac{q^{4} + 1}{q^{3} + q^{2} + q} = \frac{82}{39}$

$\Leftrightarrow q = 3, q = \frac{1}{3}$
Với q = 3 thì $u_{1} (1 + 3^{4}) = \frac{82}{11}$

$\Leftrightarrow u_{1} .82 = \frac{82}{11}$

$\Leftrightarrow u_{1} = \frac{1}{11}$
Với $q = \frac{1}{3}$ thì $u_{1} [1 + {(\frac{1}{3})}^{4}] = \frac{82}{11}$

$\Leftrightarrow u_{1} . \frac{82}{81} = \frac{82}{11}$

$\Leftrightarrow u_{1} = \frac{81}{11}$

Câu 4:

Dãy số $(u_{n})$ có phải là cấp số nhân không? Nếu phải hãy xác định số công bội ? Biết: $u_{n} = 2 n$

A. $q = 3$

B. $q = 2$

C. $q = 4$

D. $q = \emptyset$

Xem đáp án

Chọn D.

Ta có: $\frac{u_{n + 1}}{u_{n}} = \frac{n + 1}{n}$ phụ thuộc vào n suy ra dãy $(u_{n})$ không phải là cấp số nhân.

Câu 5:

Dãy số $(u_{n})$ có phải là cấp số nhân không ? Nếu phải hãy xác định số công bội ?

Biết: $u_{n} = {4.3}^{n}$

A. $q = 3$

B. $q = 2$

C. $q = 4$

D. $q = \emptyset$

Xem đáp án

Chọn A.

Ta có: $\frac{u_{n + 1}}{u_{n}} = \frac{{4.3}^{n + 1}}{{4.3}^{n}} = 3$ không phụ thuộc vào n suy ra dãy $(u_{n})$ là một cấp số nhân với công bội $q = 3$ .

Câu 6:

Dãy số $(u_{n})$ có phải là cấp số nhân không ? Nếu phải hãy xác định số công bội ?

Biết: $u_{n} = \frac{2}{n}$ .

A. $q = 3$

B. $q = \frac{1}{2}$

C. $q = 4$

D. $q = \emptyset$

Xem đáp án

Chọn D.

Ta có: $\frac{u_{n + 1}}{u_{n}} = \frac{2}{n + 1} : \frac{2}{n} = \frac{n}{n + 1}$ phụ thuộc vào n.

Suy ra dãy $(u_{n})$ không phải là cấp số nhân.

Câu 7:

Cho dãy số $\frac{- 1}{\sqrt{2}}; \sqrt{b}; \sqrt{2}$ . Chọn b để dãy số đã cho lập thành cấp số nhân?

A. $b = - 1$

B. $b = 1$

C. $b = 2$

D. Không có giá trị nào của b.

Xem đáp án

Chọn D.
Dãy số đã cho lập thành cấp số nhân khi $\{\begin{cases} b \geq 0 \\ b = - \frac{1}{\sqrt{2}} . \sqrt{2} = - 1 \end{cases} .$

Vậy không có giá trị nào của b.

Câu 8:

Cho cấp số nhân: $\frac{- 1}{5}; a; \frac{- 1}{125}$ . Giá trị của a là:

A. $a = \pm \frac{1}{\sqrt{5}}$

B. $a = \pm \frac{1}{25}$

C. $a = \pm \frac{1}{5}$

D. $a = \pm 5$

Xem đáp án

Chọn B.

Ta có: $a^{2} = (- \frac{1}{5}) . (- \frac{1}{125}) = \frac{1}{625}$

$\Leftrightarrow a = \pm \frac{1}{25}$

Câu 9:

Cho dãy số: $- 1; x; 0, 64$ . Chọn x để dãy số đã cho theo thứ tự lập thành cấp số nhân?

A. Không có giá trị nào của x

B. $x = - 0, 008$

C. $x = 0, 008$

D. $x = 0, 004$

Xem đáp án

Chọn A.

Dãy số: $-1; x; 0,64$ theo thứ tự lập thành cấp số nhân

$\Leftrightarrow x^{2} = - 0, 64$ ( Phương trình vô nghiệm)

Câu 10:

Hãy chọn cấp số nhân trong các dãy số được cho sau đây:

A.

B.

C.

D.

Xem đáp án

Chọn B.

Ta có: $u_{n} = \frac{1}{4^{n - 2}} \Rightarrow u_{n - 1} = \frac{1}{4^{n - 3}}$ .

Suy ra $\frac{u_{n}}{u_{n - 1}} = \frac{1}{4}$ ( Không đổi).

Vậy $u_{n} = \frac{1}{4^{n - 2}}$ là một cấp số nhân có công bội $q = \frac{1}{4} .$

Câu 11:

Cho dãy số: –1; 1; –1; 1; –1; … Khẳng định nào sau đây là đúng?

A. Dãy số này không phải là cấp số nhân

B. Số hạng tổng quát un = 1n =1

C. Dãy số này là cấp số nhân có $u_{1}$ = –1, q = –1

D. Số hạng tổng quát $u_{n}$ = (–1)2n.

Xem đáp án

Chọn C.

Ta có $1 = - 1 (- 1); - 1 = 1 (- 1)$ .

Vậy dãy số trên là cấp số nhân với $u_{1} = - 1; q= - 1$ .

Câu 12:

Cho dãy số : $1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16}, . . .$ Khẳng định nào sau đây là sai?

A. Dãy số này là cấp số nhân có $u_{1} = 1, q = \frac{1}{2}$

B. Số hạng tổng quát $u_{n} = \frac{1}{2^{n - 1}}$

C. Số hạng tổng quát $u_{n} = \frac{1}{2^{n}}$

D. Dãy số này là dãy số giảm

Xem đáp án

Chọn C.

Ta có $\frac{1}{2} = 1. \frac{1}{2}; \frac{1}{4} = \frac{1}{2} . \frac{1}{2};$

$\frac{1}{8} = \frac{1}{4} . \frac{1}{2}; \frac{1}{16} = \frac{1}{8} . \frac{1}{2}; ....$

Vậy daỹ số trên là cấp số nhân với $u_{1} = 1; q= \frac{1}{2}$ .
Áp dụng công thức số hạng tổng quát cấp số nân ta có :

$u_{n} = u_{1} q^{n - 1} = {(\frac{1}{2})}^{n - 1} = \frac{1}{2^{n - 1}}$

Câu 13:

Cho dãy số: –1; –1; –1; –1; –1; … Khẳng định nào sau đây là đúng?

A. Dãy số này không phải là cấp số nhân.

B. Là cấp số nhân có $u_{1} = - 1, q = 1$

C. Số hạng tổng quát $u_{n} = {(- 1)}^{n}$

D. Là dãy số giảm.

Xem đáp án

Chọn B.

Các số hạng trong dãy giống nhau nên gọi là cấp số nhân với $u_{1} = - 1; q=1.$

Câu 14:

Cho dãy số : $- 1; \frac{1}{3}; \frac{- 1}{9}; \frac{1}{27}; \frac{- 1}{81}$ . Khẳng định nào sau đây là sai?

A. Dãy số không phải là một cấp số nhân.

B. Dãy số này là cấp số nhân có $u_{1} = - 1, q = \frac{- 1}{3}$

C. Số hạng tổng quát $u_{n} = {(- 1)}^{n} . \frac{1}{3^{n - 1}}$

D. Là dãy số không tăng, không giảm.

Xem đáp án

Chọn A.

Ta có:

$\frac{1}{3} = - 1. (- \frac{1}{3}); - \frac{1}{9} = - \frac{1}{3} . (- \frac{1}{3});$

$\frac{1}{27} = - \frac{1}{9} . (- \frac{1}{3}); .......$

Vậy dãy số trên là cấp số nhân với $u_{1} = - 1; q=- \frac{1}{3}$ .
Áp dụng công thức số hạng tổng quát cấp số nhân ta có

$u_{n} = u_{1} q^{n - 1} = - 1 {(- \frac{1}{3})}^{n - 1}$

$= {(- 1)}^{n} . \frac{1}{3^{n - 1}}$

Câu 15:

Cho cấp số nhân $(u_{n})$ với $u_{1} = \frac{- 1}{2}, u_{7} = - 32$ . Tìm q ?

A. $q = \pm \frac{1}{2}$

B. $q = \pm 2$

C. $q = \pm 4$

D. $q = \pm 1$

Xem đáp án

Chọn B.

Áp dụng công thức số hạng tổng quát cấp số nhân ta có

$u_{n} = u_{1} q^{n - 1} \Rightarrow u_{7} = u_{1} . q^{6}$

$\Rightarrow q^{6} = 64 \Rightarrow [\begin{array}{l} q = 2 \\ q = - 2 \end{array}$

Câu 16:

Cho cấp số nhân $(u_{n})$ với $u_{1} = - 2; q=-5$ . Viết 3 số hạng tiếp theo và số hạng tổng quát $u_{n}$ ?

A.

B.

C.

D.

Xem đáp án

Chọn D

Ta có

$u_{2} = u_{1} . q = (- 2) . (- 5) = 10;$

$u_{3} = u_{2} . q = 10. (- 5) = - 50;$

$u_{4} = u_{3} . q = - 50. (- 5) = 250$

Số hạng tổng quát $u_{n} = u_{1} . q^{n - 1} = (- 2) . {(- 5)}^{n - 1}$ .

Câu 17:

Xét xem dãy số $u_{n} = - \frac{3^{n - 1}}{5}$ có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội.

A. $q = 3$

B. $q = 2$

C. $q = 4$

D. $q = \emptyset$

Xem đáp án

Chọn A.

Ta có: $\frac{u_{n + 1}}{u_{n}} = 3 \Rightarrow (u_{n})$ là CSN với công bội $q = 3$

Câu 18:

Cho cấp số nhân $(u_{n})$ với $u_{1} = - 1, q = 0, 00001$ . Tìm q và $u_{n}$ ?

A.

B.

C.

D.

Xem đáp án

Chọn D.

Ta có $u_{6} = u_{1} . q^{5}$

$\Rightarrow 0, 00001 = - 1. q^{5}$

$\Rightarrow q = - \frac{1}{10}$
Số hạng tổng quát

$u_{n} = u_{1} . q^{n - 1}$

$= - 1. {(- \frac{1}{10})}^{n - 1} = \frac{{(- 1)}^{n}}{10^{n - 1}}$

Câu 19:

Cho cấp số nhân $(u_{n})$ với $u_{1} = - 1, q = \frac{- 1}{10}$ . Số $\frac{1}{10^{103}}$ là số hạng thứ mấy của $(u_{n})$ ?

A. Số hạng thứ 103

B. Số hạng thứ 104

C. Số hạng thứ 105

D. Không là số hạng của cấp số đã cho.

Xem đáp án

Chọn B.

Ta có $u_{n} = u_{1} . q^{n - 1}$

$\Rightarrow \frac{1}{10^{103}} = - 1. {(- \frac{1}{10})}^{n - 1}$

$\Rightarrow n - 1 = 103 \Rightarrow n = 104$

Câu 20:

Cho cấp số nhân $(u_{n})$ với $u_{1} = 3, q = - 2$ . Số 192 là số hạng thứ mấy của $(u_{n})$ ?

A. Số hạng thứ 5.

B. Số hạng thứ 6.

C. Số hạng thứ 7.

D. Không là số hạng của cấp số đã cho.

Xem đáp án

Chọn C.

Ta có $u_{n} = u_{1} . q^{n - 1}$

$\Rightarrow \frac{1}{10^{103}} = - 1. {(- \frac{1}{10})}^{n - 1}$

$\Rightarrow n - 1 = 103 \Rightarrow n = 104$

Câu 21:

Cho cấp số nhân $(u_{n})$ với $u_{1} = 3, q = \frac{- 1}{2}$ . Số 222 là số hạng thứ mấy của $(u_{n})$ ?

A. Số hạng thứ 11

B. Số hạng thứ 12

C. Số hạng thứ 9

D. Không là số hạng của cấp số đã cho

Xem đáp án

Chọn D.

Ta có $u_{n} = u_{1} . q^{n - 1}$

$\Rightarrow 222 = 3. {(- \frac{1}{2})}^{n - 1}$

$\Rightarrow {(- \frac{1}{2})}^{n - 1} = 74$

Vậy 222 không là số hạng của cấp số đã cho.

Câu 22:

Cho cấp số nhân ( $u_{n}$ ) có các số hạng khác không, tìm $u_{1}$ biết: $\{\begin{cases} u_{1} + u_{2} + u_{3} + u_{4} = 15 \\ {u_{1}}^{2} + {u_{2}}^{2} + {u_{3}}^{2} + {u_{4}}^{2} = 85 \end{cases}$

A. $u_{1} = 1, u_{1} = 2$

B. $u_{1} = 1, u_{1} = 8$

C. $u_{1} = 1, u_{1} = 5$

D. $u_{1} = 1, u_{1} = 9$

Xem đáp án

Chọn B.

Câu 23:

Xét xem dãy số sau có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội.

$u_{n} = 3 n - 1$

A. $q = 3$

B. $q = 2$

C. $q = 4$

D. $q = \emptyset$

Xem đáp án

Chọn D.

Ta có: $\frac{u_{n + 1}}{u_{n}} = \frac{3 n + 2}{3 n - 1}$

$\Rightarrow (u_{n})$ không phải là CSN

Câu 24:

Xét xem dãy số sau có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội.

$u_{n} = \frac{2^{n} - 1}{3}$

A. $q = 3$

B. $q = 2$

C. $q = 4$

D. $q = \emptyset$

Xem đáp án

Chọn D.

Ta có: $\frac{u_{n + 1}}{u_{n}} = \frac{2^{n + 1} - 1}{2^{n} - 1}$

$\Rightarrow (u_{n})$ không phải là CSN

Câu 25:

Xét xem dãy số $u_{n} = n^{3}$ có phải là cấp số nhân hay không? Nếu phải hãy xác định công bội.

A. $q = 3$

B. $q = 2$

C. $q = 4$

D. $q = \emptyset$

Xem đáp án

Chọn D.

Ta có: $\frac{u_{n + 1}}{u_{n}} = \frac{{(n + 1)}^{3}}{n^{3}}$

$\Rightarrow (u_{n})$ không phải là CSN.

Câu 26:

Cho cấp số nhân có $u_{1} = - 3$ , $q = \frac{2}{3}$ . Tính $u_{5} ?$

A. $u_{5} = \frac{- 27}{16}$

B. $u_{5} = \frac{- 16}{27}$

C. $u_{5} = \frac{16}{27}$

D. $u_{5} = \frac{27}{16}$

Xem đáp án

Chọn B.

Ta có:

$u_{5} = u_{1} . q^{4} = (- 3) {(\frac{2}{3})}^{4} = - \frac{16}{27} .$

Câu 27:

Cho cấp số nhân có $u_{1} = - 3, q = \frac{2}{3}$ . Số $\frac{- 96}{243}$ là số hạng thứ mấy của cấp số này?

A. Thứ 5.

B. Thứ 6.

C. Thứ 7.

D. Không phải là số hạng của cấp số.

Xem đáp án

Chọn B.

Giả sử số $\frac{- 96}{243}$ là số hạng thứ n của cấp số này.
Ta có: $u_{1} . q^{n - 1} = \frac{- 96}{243}$

$\Leftrightarrow (- 3) {(\frac{2}{3})}^{n - 1} = \frac{- 96}{243}$

$\Leftrightarrow n = 6$
Vậy số $\frac{- 96}{243}$ là số hạng thứ 6 của cấp số.

Câu 28:

Cho cấp số nhân có $u_{2} = \frac{1}{4}, u_{5} = 16$ ; . Tìm q và $u_{1}$

A.

B.

C.

D.

Xem đáp án

Chọn C.

Ta có: $u_{2} = u_{1} . q \Leftrightarrow \frac{1}{4} = u_{1} . q$

$u_{5} = u_{1} . q^{4} \Leftrightarrow 16 = u_{1} . q^{4}$
Suy ra: $q^{3} = 64 \Leftrightarrow q = 4$ . Từ đó: $u_{1} = \frac{1}{16} .$

Câu 29: