Trắc nghiệm Bất phương trình bậc nhất hai ẩn (có đáp án)
Trắc nghiệm Toán 10 Bài 4: Bất phương trình bậc nhất hai ẩn
-
2219 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Câu nào sau đây đúng?
Miền nghiệm của hệ bất phương trình {x2+y3−1≥02(x−1)+3y2≤4x≥0 là phần mặt phẳng chứa điểm
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Nhận xét: chỉ có điểm (2;1) thỏa mãn hệ.
Câu 2:
15/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Nhận xét : chỉ có điểm (0;0) không thỏa mãn hệ.
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Nhận xét: chỉ có điểm (0;−2) thỏa mãn hệ.
Câu 4:
23/07/2024Câu nào sau đây sai?.
Miền nghiệm của bất phương trình −x+2+2(y−2)<2(1−x) là nửa mặt phẳng chứa điểm
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có:
−x+2+2(y−2)<2(1−x)
⇔−x+2+2y−4<2−2x
⇔x+2y<4
Dễ thấy tại điểm (4; 2) ta có: 4+2.2=8>4.
Câu 5:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
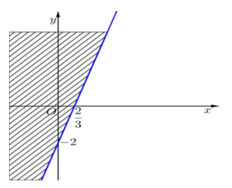
Trước hết, ta vẽ đường thẳng (d):−3x+y+2=0.
Ta thấy (0;0) không là nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mặt phẳng bờ (d) không chứa điểm (0;0) .
Câu 6:
16/10/2024Câu nào sau đây đúng?.
Miền nghiệm của bất phương trình 3(x−1)+4(y−2)<5x−3 là nửa mặt phẳng chứa điểm
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Phương pháp giải
- Để xét miền nghiệm của bất phương trình, trước tiên ta thực hiện phép nhân để phá dấu ngoặc ra rồi thực hiện chuyển hết về 1 vế và thực hiện phép tính rút gọn
- bất phương trình chuyển về dạng Ax + b >0. Xem các nghiệm của 4 đáp án xem đáp án nào thỏa mãn
*Lời giải
Ta có:
3(x−1)+4(y−2)<5x−3
⇔3x−3+4y−8<5x−3
⇔2x−4y+8>0
⇔x−2y+4>0
Dễ thấy tại điểm (0;0) ta có:
0−2.0+4=4>0
* Lý thuyết cần nắm và các dạng bài về bất phương trình bậc nhất hai ẩn:
Bất phương trình bậc nhất hai ẩn
- Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là:
ax+by≤c(ax+by≥c,ax+by<c,ax+by>c)ax+by≤c(ax+by≥c,ax+by<c,ax+by>c)
Trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
- Cặp số (x0;y0)(x0;y0) được gọi là một nghiệm của bất phương trình bậc nhất hai ẩn ax+by≤cax+by≤c nếu bất đẳng thức ax0+by0≤cax0+by0≤c đúng.
Nhận xét: Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
Dạng 1: Giải và biện luận bất phương trình bậc nhất
Phương pháp giải:
- Bất phương trình bậc nhất là bất phương trình có dạng:ax+b>0, ax+b<0,ax+b>0, ax+b<0, ax+b≥0, ax+b≤0ax+b≥0, ax+b≤0 với a, b∈R.a, b∈ℝ.
- Giải và biện luận bất phương trình dạng: ax+b>0ax+b>0 (1).
+) Nếu a>0a>0 thì (1)⇔ax>−b⇔x>−ba(1)⇔ax>−b⇔x>−ba
⇒⇒Tập nghiệm của bất phương trình là S=(−ba;+∞)⋅S=(−ba;+∞)⋅
+) Nếu a<0a<0 thì (1)⇔ax>−b⇔x<−ba(1)⇔ax>−b⇔x<−ba
⇒⇒Tập nghiệm của bất phương trình là S=(−∞;−ba)⋅S=(−∞;−ba)⋅
+) Nếu a=0 thì (1)⇔0.x>−b.(1)⇔0.x>−b. Khi đó, ta xét:
Với −b≥0⇒−b≥0⇒ Tập nghiệm của bất phương trình là S=∅S=∅
Với −b<0⇒−b<0⇒ Tập nghiệm của bất phương trình là S=R
Dạng 2: Dấu của nhị thức bậc nhất
Phương pháp giải:
- Nhị thức bậc nhất đối với x là biểu thức dạng f(x) = ax + b trong đó a, b là hai số đã cho, a≠0a≠0.
- Định lý về dấu của nhị thức bậc nhất: Nhị thức f(x) = ax + b (a≠0a≠0) cùng dấu với hệ số a khi x lấy các giá trị trong khoảng (−ba,+∞)(−ba,+∞) và trái dấu với hệ số a khi x lấy các giá trị trong khoảng (−∞,−ba)(−∞,−ba).
Ta có bảng xét dấu của nhị thức f(x) = ax + b (a≠0a≠0) như sau:

Minh họa bằng đồ thị
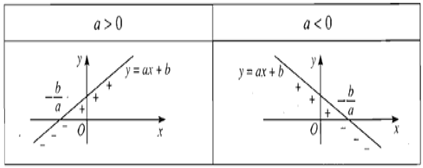
Xem thêm trong file bài viết lý thuyết ở dưới
Xem thêm các bài viết liên quan hay chi tiết:
Bất phương trình bậc nhất và cách giải bài tập chi tiết nhất
Giải Toán 10 Bài 3 SGK (Kết nối tri thức): Bất phương trình bậc nhất hai ẩn
Câu 7:
23/07/2024Câu nào sau đây sai?.
Miền nghiệm của bất phương trình x+3+2(2y+5)<2(1−x) là nửa mặt phẳng chứa điểm
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có:
x+3+2(2y+5)<2(1−x)
⇔x+3+4y+10<2−2x
⇔3x+4y+8<0
Dễ thấy tại điểm (0;0) ta có: 3.0+4.0+8>0 (mâu thuẩn).
Câu 8:
16/10/2024 Xem đáp án
Xem đáp án
Đáp án đúng: C
*Phương pháp giải
- để vẽ được miền nghiệm của bất phương trình ta vẽ đường thẳng 3x-2y=-6 trên mặt phẳng tọa độ Oxy trước
- Xét điểm (0,0) vào bất phương trình ta thấy (0,0) là một nghiệm. vậy miền chính là bờ nằm phía chứa (0,0)
*Lời giải
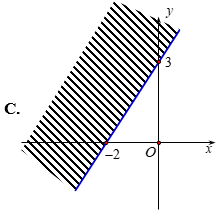
Trước hết, ta vẽ đường thẳng (d):3x−2y=−6.
Ta thấy (0;0) là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ (d) chứa điểm (0;0).
* Lý thuyết cần nắm và các dạng bài về bất phương trình bậc nhất hai ẩn:
Bất phương trình bậc nhất hai ẩn
- Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là:
ax+by≤c(ax+by≥c,ax+by<c,ax+by>c)ax+by≤c(ax+by≥c,ax+by<c,ax+by>c)ax+by≤c(ax+by≥c,ax+by<c,ax+by>c)
Trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
- Cặp số (x0;y0)(x0;y0)(x0;y0) được gọi là một nghiệm của bất phương trình bậc nhất hai ẩn ax+by≤cax+by≤cax+by≤c nếu bất đẳng thức ax0+by0≤cax0+by0≤cax0+by0≤c đúng.
Nhận xét: Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm
Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
- Trong mặt phẳng tọa độ Oxy, tập hợp các điểm (x0; y0) sao cho ax0 + by0 + c < 0 được gọi là miền nghiệm của bất phương trình ax + by + c < 0.
- Người ta chứng minh được: Mỗi phương trình ax + by + c = 0 (a, b không đồng thời bằng 0) xác định một đường thẳng ∆. Đường thẳng ∆ chia mặt phẳng tọa độ Oxy thành hai nửa mặt phẳng, trong đó một nửa (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c > 0, nửa còn lại (không kể bờ ∆) là tập hợp các điểm (x; y) thỏa mãn ax + by + c < 0.
Ta có thể biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ax + by + c < 0 như sau:
Bước 1: Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng ∆: ax + by +c = 0.
Bước 2: Lấy một điểm (x0; y0) không thuộc ∆. Tính ax0 +by0 + c.
+ Nếu ax0 + by0 + c < 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) chứa điểm (x0; y0).
+ Nếu ax0 + by0 + c > 0 thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ ∆) không chứa điểm (x0; y0).
Chú ý: Đối với các bất phương trình bậc nhất hai ẩn dạng ax + by + c ≤ 0 (hoặc ax + by + c ≥ 0) thì miền nghiệm là miền nghiệm của bất phương trình ax + by + c < 0 (hoặc ax + by + c > 0) kể cả bờ.
Xem thêm các bài viết liên quan hay chi tiết:
Bất phương trình bậc nhất và cách giải bài tập chi tiết nhất
Câu 9:
23/07/2024Câu nào sau đây đúng?.
Miền nghiệm của bất phương trình 4(x−1)+5(y−3)>2x−9 là nửa mặt phẳng chứa điểm
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có:
4(x−1)+5(y−3)>2x−9
⇔4x−4+5y−15>2x−9
⇔2x+5y−10>0
Dễ thấy tại điểm (2;5) ta có: 2.2+5.5−10>0 (đúng).
Câu 10:
16/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta thấy (√22;0)∈S
vì −2.√22+√3.0+√2=0
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta thấy (1;−12)∈S
vì {1−12>02.1+5.(−12)<0.
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta thấy (−1;√5)∉S vì −1<0
Câu 13:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải
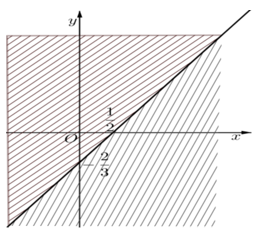
Trước hết, ta vẽ hai đường thẳng:
(d1):2x−32y=1
(d2):4x−3y=2
Thử trực tiếp ta thấy (0;0) là nghiệm của phương trình (2) nhưng không phải là nghiệm của phương trình (1). Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của bất phương trình chính là các điểm thuộc đường thẳng (d):4x−3y=2.
Câu 14:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải
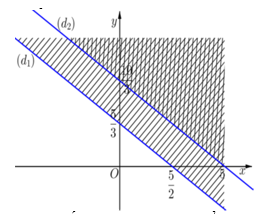
Trước hết, ta vẽ hai đường thẳng:
(d1):2x+3y=5
(d2):x+32y=5
Ta thấy (0;0) là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Say khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ.
Câu 15:
23/07/2024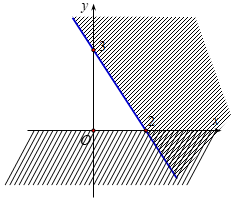
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng (d1):y=0 và đường thẳng (d2):3x+2y=6.
Miền nghiệm gồm phần y nhận giá trị dương.
Lại có (0;0) thỏa mãn bất phương trình 3x+2y<6.
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải
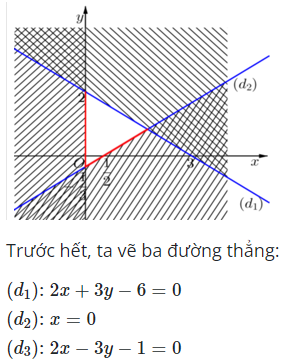
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
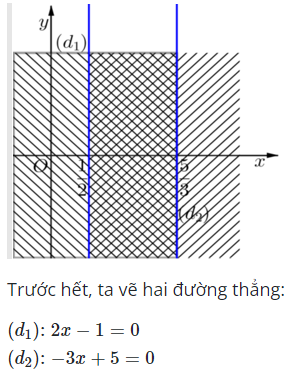
Câu 18:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Biểu diễn miền nghiệm của hệ bất phương trình {y−2x≤22y−x≥4x+y≤5 trên hệ trục tọa độ như dưới đây:
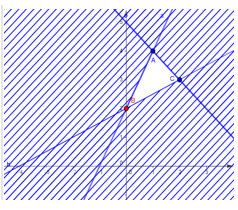
Nhận thấy biết thức F=y−x chỉ đạt giá trị nhỏ nhất tại các điểm A,B hoặc C.
Ta có:
F(A)=4−1=3; F(B)=2; F(C)=3−2=1
Vậy min F=1 khi x=2,y=3.
Câu 19:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Biểu diễn miền nghiệm của hệ bất phương trình {2x+y≤2x−y≤25x+y≥−4 trên hệ trục tọa độ như dưới đây:
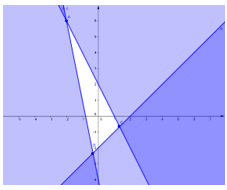
Giá trị nhỏ nhất của biết thức F=y−x chỉ đạt được tại các điểm
A(−2;6),C(43;−23), B(−13;−73)
Ta có:
F(A)=8; F(B)=−2; F(C)=−2
Vậy min F=−2 khi x=43,y=−23.
Câu 20:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải
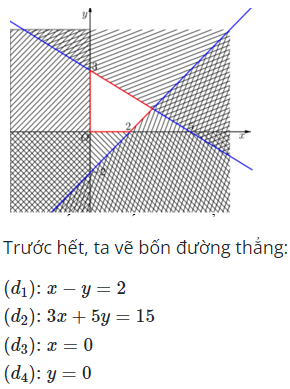
Có thể bạn quan tâm
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn (có đáp án) (2218 lượt thi)
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn có đáp án (440 lượt thi)
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn 10 có đáp án (375 lượt thi)
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn có đáp án (Nhận biết) (434 lượt thi)
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn có đáp án (Thông hiểu) (443 lượt thi)
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn có đáp án (Vận dụng) (518 lượt thi)
Các bài thi hot trong chương
- 75 câu trắc nghiệm Bất đẳng thức - Bất phương trình nâng cao (1284 lượt thi)
- Trắc nghiệm Dấu của nhị thức bậc nhất (có đáp án) (609 lượt thi)
- Trắc nghiệm Dấu của tam thức bậc hai (có đáp án) (591 lượt thi)
- Trắc nghiệm Bất đẳng thức (có đáp án) (508 lượt thi)
- Trắc nghiệm Bất đẳng thức có đáp án (Nhận biết) (503 lượt thi)
- Trắc nghiệm Bất đẳng thức có đáp án (497 lượt thi)
- Trắc nghiệm Bất phương trình và hệ bất phương trình một ẩn có đáp án (Tổng hợp) (488 lượt thi)
- Trắc nghiệm Ôn tập Toán 10 Chương 4 có đáp án (Tổng hợp) (455 lượt thi)
- Trắc nghiệm Bất phương trình và hệ bất phương trình một ẩn (có đáp án) (451 lượt thi)
- Trắc nghiệm Dấu của tam thức bậc hai có đáp án (Thông hiểu) (446 lượt thi)
