Câu hỏi:
16/10/2024 2,348Câu nào sau đây đúng?.
Miền nghiệm của bất phương trình 3(x−1)+4(y−2)<5x−3 là nửa mặt phẳng chứa điểm
A. (0;0).
B. (-4;2).
C. (-2;2).
D. (-5;3)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Phương pháp giải
- Để xét miền nghiệm của bất phương trình, trước tiên ta thực hiện phép nhân để phá dấu ngoặc ra rồi thực hiện chuyển hết về 1 vế và thực hiện phép tính rút gọn
- bất phương trình chuyển về dạng Ax + b >0. Xem các nghiệm của 4 đáp án xem đáp án nào thỏa mãn
*Lời giải
Ta có:
3(x−1)+4(y−2)<5x−3
⇔3x−3+4y−8<5x−3
⇔2x−4y+8>0
⇔x−2y+4>0
Dễ thấy tại điểm (0;0) ta có:
0−2.0+4=4>0
* Lý thuyết cần nắm và các dạng bài về bất phương trình bậc nhất hai ẩn:
Bất phương trình bậc nhất hai ẩn
- Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là:
Trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
- Cặp số được gọi là một nghiệm của bất phương trình bậc nhất hai ẩn nếu bất đẳng thức đúng.
Nhận xét: Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
Dạng 1: Giải và biện luận bất phương trình bậc nhất
Phương pháp giải:
- Bất phương trình bậc nhất là bất phương trình có dạng: với
- Giải và biện luận bất phương trình dạng: (1).
+) Nếu thì
Tập nghiệm của bất phương trình là
+) Nếu thì
Tập nghiệm của bất phương trình là
+) Nếu a=0 thì Khi đó, ta xét:
Với Tập nghiệm của bất phương trình là
Với Tập nghiệm của bất phương trình là
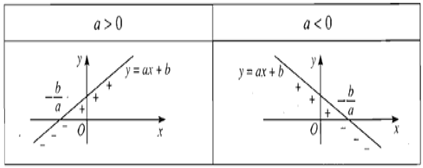
Dạng 2: Dấu của nhị thức bậc nhất
Phương pháp giải:
- Nhị thức bậc nhất đối với x là biểu thức dạng f(x) = ax + b trong đó a, b là hai số đã cho, .
- Định lý về dấu của nhị thức bậc nhất: Nhị thức f(x) = ax + b () cùng dấu với hệ số a khi x lấy các giá trị trong khoảng và trái dấu với hệ số a khi x lấy các giá trị trong khoảng .
Ta có bảng xét dấu của nhị thức f(x) = ax + b () như sau:

Minh họa bằng đồ thị
Xem thêm trong file bài viết lý thuyết ở dưới
Xem thêm các bài viết liên quan hay chi tiết:
Bất phương trình bậc nhất và cách giải bài tập chi tiết nhất
Giải Toán 10 Bài 3 SGK (Kết nối tri thức): Bất phương trình bậc nhất hai ẩn
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Giá trị nhỏ nhất của biết thức F=y−x trên miền xác định bởi hệ {2x+y≤2x−y≤25x+y≥−4 là
Câu 2:
Miền nghiệm của hệ bất phương trình {2x+3y−6<0x≥02x−3y−1≤0 chứa điểm nào sau đây?
Câu 4:
Cho hệ bất phương trình {x+y>02x+5y<0 có tập nghiệm là S. Khẳng định nào sau đây là khẳng định đúng?
Câu 5:
Câu nào sau đây sai?.
Miền nghiệm của bất phương trình x+3+2(2y+5)<2(1−x) là nửa mặt phẳng chứa điểm
Câu nào sau đây sai?.
Miền nghiệm của bất phương trình x+3+2(2y+5)<2(1−x) là nửa mặt phẳng chứa điểm
Câu 6:
Miền nghiệm của bất phương trình −3x+y+2≤0 không chứa điểm nào sau đây?
Câu 7:
Cho hệ bất phương trình {x>0x+√3y+1≤0 có tập nghiệm là S. Khẳng định nào sau đây là khẳng định đúng?
Câu 8:
Cho hệ bất phương trình {x−y≤23x+5y≤15x≥0y≥0. Khẳng định nào sau đây là khẳng định sai
Câu 9:
Cho hệ {2x+3y<5 (1)x+32y<5 (2). Gọi S1 là tập nghiệm của bất phương trình (1), S2 là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì
Câu 10:
Miền nghiệm của hệ bất phương trình {2x−1≤0−3x+5≤0 chứa điểm nào sau đây?
Câu 11:
Câu nào sau đây sai?.
Miền nghiệm của bất phương trình −x+2+2(y−2)<2(1−x) là nửa mặt phẳng chứa điểm
Câu nào sau đây sai?.
Miền nghiệm của bất phương trình −x+2+2(y−2)<2(1−x) là nửa mặt phẳng chứa điểm
Câu 12:
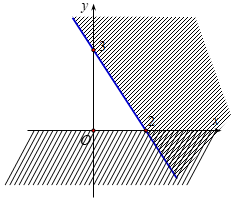
Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D ?

Câu 13:
Câu nào sau đây đúng?.
Miền nghiệm của bất phương trình 4(x−1)+5(y−3)>2x−9 là nửa mặt phẳng chứa điểm
Câu nào sau đây đúng?.
Miền nghiệm của bất phương trình 4(x−1)+5(y−3)>2x−9 là nửa mặt phẳng chứa điểm
Câu 14:
Cho hệ bất phương trình {2x−32y≥14x−3y≤2 có tập nghiệm S. Khẳng định nào sau đây là khẳng định đúng ?
Câu 15:
Câu nào sau đây đúng?
Miền nghiệm của hệ bất phương trình {x2+y3−1≥02(x−1)+3y2≤4x≥0 là phần mặt phẳng chứa điểm
Câu nào sau đây đúng?
Miền nghiệm của hệ bất phương trình {x2+y3−1≥02(x−1)+3y2≤4x≥0 là phần mặt phẳng chứa điểm


