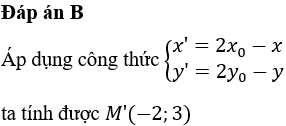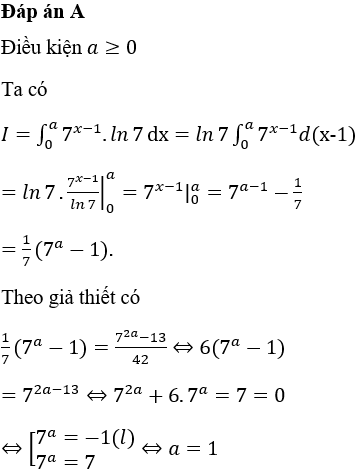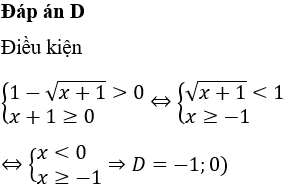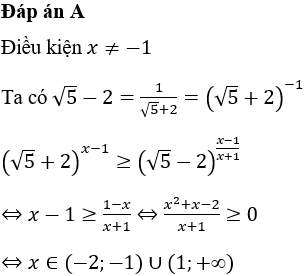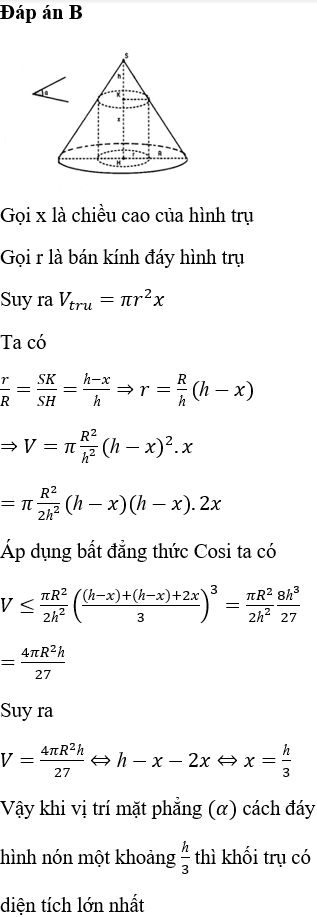Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 5)
-
2954 lượt thi
-
50 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Trong mặt phẳng Oxy, phép đối xứng tâm O biến điểm M(2;-3) thành điểm nào sau đây.
Câu 3:
21/07/2024Biển số xe ở thành phố X có cấu tạo như sau: Phần đầu là hai chữ cái trong bảng chữ cái tiếng Anh (có 26 chữ cái) Phần đuôi là 5 chữ số lấy từ {0;1;2;...;9}. Ví dụ HA 135.67 Hỏi có thể tạo được bao nhiêu biển số xe theo cấu tạo như trên
 Xem đáp án
Xem đáp án
Đáp án C
Để tạo một biển số xe ta thực hiện các bước sau:
+ Chọn hai chữ cái cho phần đầu có (mỗi chữ có 26 cách chọn)
+ Chọn 5 chữ số cho phần đuôi có (mỗi chữ số có 10 cách chọn)
Vậy có thể tạo ra được biển số xe
Câu 7:
30/10/2024Biết rằng một hình đa diện H có 6 mặt là 6 tam giác đều. Hãy chỉ ra mệnh đề nào dưới đây là đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là B
*Lời giải
Luôn tồn tại một hình đa diện H có 4 mặt phẳng đối xứng và có đúng 5 đỉnh, H không có tâm đối xứng
*Phương pháp giải
- nắm lại lý thuyết về hình đa diện: một hình đa diện có 4 mặt phẳng đối xứng và có đúng 5 đỉnh
*Lý thuyết cần nắm và dạng bài toán về khối đa diện:
Khái niệm về hình đa diện
Hình đa diện (gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất sau:
a) Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
- Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là đỉnh, cạnh của hình đa diện.
Khái niệm về khối đa diện
- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.
Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
- Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.
Một số kết quả quan trọng
a) Một khối đa diện bất kì có ít nhất 4 mặt.
b) Mỗi hình đa diện có ít nhất 4 đỉnh.
c) Mỗi hình đa diện có ít nhất 6 cạnh.
d) Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất 3 cạnh.
e) Không tồn tại hình đa diện có 7 cạnh.
f) Cho (H) là đa diện mà các mặt của nó là những đa giác có p cạnh. Nếu số mặt của (H) là lẻ thì (p) phải là số chẵn.
g) Cho (H) là đa diện có m mặt, mà các mặt của nó là những đa giác có p cạnh. Khi đó số cạnh của (H) là : C=pM2
h) Mỗi khối đa diện có các mặt là các tam giác thì tổng số các mặt của nó phải là một số chẵn.
i) Mỗi khối đa diện bất kì luôn có thể được phân chia được thành những khối tứ diện.
k) Nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số chẵn.
(Tổng quát : Một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của một số lẻ mặt thì tổng số đỉnh là một số chẵn).
l) Không tồn tại một hình đa diện có:
+ Số mặt lớn hơn hoặc bằng số cạnh;
+ Số đỉnh lớn hơn hoặc bằng số cạnh.
CÁC DẠNG BÀI VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Nhận diện khối đa diện
Phương pháp: Ta dựa vào định nghĩa và các kết quả quan trọng ở phần lý thuyết.
Dạng 2: Xác định số đỉnh, cạnh, mặt bên của một khối đa diện
Phương pháp: Ta sử dụng các kết quả thừa nhận trên phần lý thuyết.
Dạng 3: Xác định mặt phẳng đối xứng
Phương pháp: Do tính chất đối xứng nhau, nên ta sẽ đi từ trung điểm của các cạnh để tìm. Đảm bảo rằng, nếu chọn 1 mặt phẳng đối xứng nào thì các điểm còn lại phải chia đều về hai phía.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Khái niệm về khối đa diện (mới 2024 + Bài Tập) – Toán 12
50 bài toán về nhận dạng khối đa diện (có đáp án 2024) – Toán 12
Câu 23:
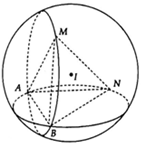
20/07/2024Cho hai đường tròn lần lượt chứa trong hai mặt phẳng phân biệt có hai điểm chung A, B. Hỏi có bao nhiêu mặt cầu có thể đi qua ?
 Xem đáp án
Xem đáp án
Đáp án B
Trên hai đường tròn lần lượt lấy M, N sao cho hai điểm này không trùng hai điểm A, B. Khi đó 4 điểm M, N, A, B không đồng phẳng nên tạo thành tứ diện ABMN. Mặt cầu (S) đi qua khi đó mặt (S) đi qua A, B, M, N
Do đó có duy nhất 1 mặt cầu
Câu 24:
22/07/2024Biết số nguyên tố có các chữ số theo thứ tự lần lượt lập thành cấp số nhân. Giá trị là
 Xem đáp án
Xem đáp án
Đáp án B
Số đó là 421, đây là số nguyên tố (chỉ chia hết cho 1 và chính nó)
Ta thấy 4, 2, 1 theo thứ tự lần lượt lập thành cấp số nhân có công bội
Giá trị là 21
Bài thi liên quan
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 1)
-
49 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 2)
-
50 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 3)
-
50 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 4)
-
50 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 6)
-
50 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 7)
-
50 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 8)
-
50 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 9)
-
50 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 10)
-
50 câu hỏi
-
60 phút
-
-
Tổng hợp đề thi thử THPTQG môn Toán cực hay chọn lọc, có lời giải chi tiết (đề số 11)
-
50 câu hỏi
-
60 phút
-