• Logo VietJack.me
×
Trang chủ Thi thử THPT Quốc gia Toán Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (24 đề)

Bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (24 đề)

24 bộ đề thi thử môn Toán THPT Quốc gia năm 2022 có lời giải (đề 14)

  • 4137 lượt thi

  • 10 câu hỏi

  • 90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

17/07/2024

Một khối lập phương lớn có thể tích bằng V, diện tích xung quanh bằng S. Người ta lấy đi một khối lập phương nhỏ có thể tích bằng 14V  như hình vẽ bên. Diện tích xung quanh hình còn lại bằng
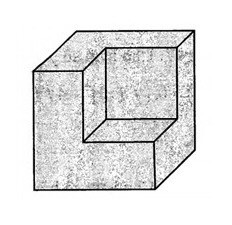
Xem đáp án

Khi mất đi 3 mặt nhỏ lại bù vào đủ 3 mặt có cùng diện tích nên diện tích xung quanh không đổi và bằng S.

Câu 2:

17/07/2024

Cho hai số phức z1=2−3i   và z2=5+2i  . Tìm số phức z=z12+z2 
Xem đáp án

Ta có: z=z12+z2=2−3i2+5+2i=4−12i+9i2+5+2i=−10i

Câu 3:

22/07/2024

Cho hàm số y=f(x) có bảng biến thiên như hình vẽ

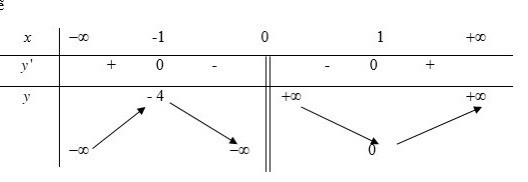
Mệnh đề nào sau đây đúng?
Xem đáp án

Dựa vào bảng biến thiên ta thấy:

Hàm số đồng biến trên các khoảng −∞;−1  và 1;+∞.

Hàm số nghịch biến trên các khoảng −1;0  và 0;1.

Câu 4:

23/07/2024

Trong không gian Oxyz, cho ba điểm  A1;−3;5, B2;0;1,C0;9;3.Tọa độ trọng tâm G của tam giác ABC là
Xem đáp án

Theo công thức tọa độ trọng tâm ta có: xG=xA+xB+xC3=1+2+03=1yG=yA+yB+yC3=−3+0+93=2zG=zA+zB+zC3=5+1+33=3⇒G1;2;3

Câu 5:

15/07/2024

Họ nguyên hàm của các hàm số  fx=e4x+1 là
Xem đáp án

Ta có: ∫fxdx=∫e4x+1dx=14∫e4xd4x+∫dx=14e4x+x+C

Câu 6:

14/07/2024

Cho hàm số y=x3−3x2−9x+2  . Mệnh đề nào sau đây là đúng?
Xem đáp án

Tập xác định D=R

y'=3x2−6x−9. Cho y'=0⇔x=−1x=3

Bảng biến thiên:

 

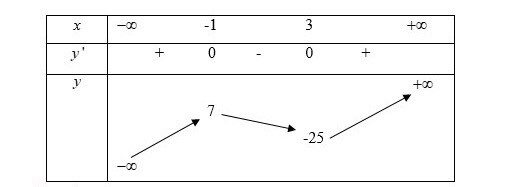
Dựa vào bảng biến thiên thì hàm số đã cho đồng biến trên khoảng 5;+∞

Câu 7:

12/07/2024

Trong không gian Oxyz, cho đường thẳng d:x+12=y1=z−21,   mặt phẳng P:x+y−2z+5=0  và A1;−1;2 . Đường thẳng Δ  cắt d và (P) lần lượt tại M và N sao cho A là trung điểm của đoạn thẳng MN. Một vecto chỉ phương của Δ  là
Xem đáp án

Điểm M∈d⇒M−1+2t;t;2+t, A là trung điểm của MN⇒N3−2t;−2−t;2−t

Điểm N∈P⇒3−2t−2−t−22−t+5=0⇔t=2⇒M(3;2;4),  N(−1;−4;0)

⇒MN→=−4;−6;−4=−22;3;2

Câu 8:

17/07/2024

Thể tích khối chóp S.ABC có độ dài các cạnh SA=BC=5, SB=AC=6, SC=AB=4   là

Xem đáp án

Áp dụng công thức V=212a2+b2−c2.a2−b2+c2.b2+c2−a2

Với a=SA=5,b=SB=6,c=SC=4⇒V=1564

Câu 9:

19/07/2024

Tất cả các giá trị của m để hàm số  y=13x3−2m−1x2+m+2x+m−6 đồng biến trên R là

Xem đáp án

Ta có y'=x2−4m−1x+m+2

Hàm số đồng biến trên R khi và chỉ khi a=1>0Δ'=4m−12−m+2=4m2−9m+2≤0⇔14≤m≤2

Câu 10:

21/07/2024

Giá trị lớn nhất của hàm số y=exx2−x−5   trên [1;3] là
Xem đáp án

Ta có y'=exx2+x−6⇒y'=0⇔x=2∈1;3x=−3∉1;3

y1=−5e;y=−3e2;y3=e3. Vậy giá trị lớn nhất là max[1;3]y=y3=e3

Bắt đầu thi ngay

Bài thi liên quan