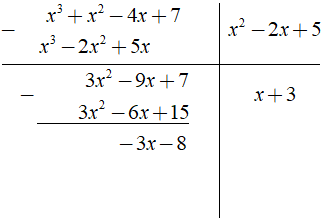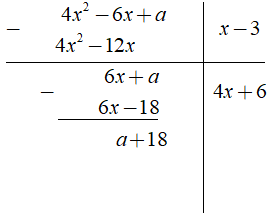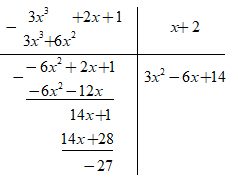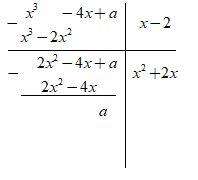Bài tập Chia đa thức một biến đã sắp xếp
-
456 lượt thi
-
18 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
23/07/2024Phép chia cho được đa thức dư là ?
Xem đáp án
Ta có phép chia
Dựa vào kết quả của phép chia trên, ta có đa thức dư là - 3x - 8.
Chọn đáp án B.
Câu 3:
22/07/2024Hệ số a thỏa mãn để chia hết cho x - 3 là ?
Xem đáp án
Ta có phép chia
Phép chia trên có số dư là ( a + 18 )
Để chia hết cho x - 3 ⇔ a + 18 = 0 ⇔ a = - 18.
Chọn đáp án A.
Câu 5:
15/07/2024Thực hiện phép chia ta được đa thức dư là:
Xem đáp án
Ta có:
Vậy số dư của phép chia đã cho là –27
Chọn đáp án D
Câu 7:
15/07/2024Cho phép chia: . Tìm khẳng định sai?
Xem đáp án
Vậy phép chia đã cho là phép chia hết có thương là:
Chọn đáp án D
Câu 9:
16/07/2024Tìm a để phép chia là phép chia hết:
Xem đáp án
Ta có:
Để phép chia đã cho là phép chia hết khi và chỉ khi phần dư bằng 0. Do đó, a =0
Chọn đáp án A
Câu 11:
16/07/2024Phần dư của phép chia đa thức cho đa thức x + 1 là
Xem đáp án
Ta có đa thức chưa (x + 1) nên phần dư là một hằng số
Gọi thương là Q(x) và dư r. Khi đó với mọi x ta có
Thay x = -1 vào (1) ta được
– 1 = Q(x).(-1 + 1) + r
r = – 1 ó r = 0
vậy phần dư của phép chia là r = 0.
đáp án cần chọn là: C
Câu 12:
15/07/2024Cho đa thức f(x) = + ax + b và đa thức g(x) = – 3x + 4. Biết f(x) chia hết cho g(x). Khi đó tích a.b bằng
Xem đáp án
Ta có
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó
ó => ab = -12
Đáp án cần chọn là: A
Câu 13:
19/07/2024Tìm đa thức bị chia biết đa thức chia là ( + x + 1),thương là (x + 3), dư là x – 2.
Xem đáp án
Đa thức bị chia cần tìm là:
( + x + 1)(x + 3) + x – 2
= + x.x+ 3x + x + 3 + x – 2
= + 5x + 1
Đáp án cần chọn là: A
Câu 14:
18/07/2024Rút gọn và tính giá trị biểu thức A = ( – 2x) : ( + ) tại x = 3.
Xem đáp án
Tại x = 3, ta có: A = 4x = 4.3 = 12
Đáp án cần chọn là: D
Câu 15:
17/07/2024Xác định a để ( – x + a) : (2x + 1) dư 2
Xem đáp án
Để – x + a chia 2x + 1 dư 2 thì a – 2 = 2 ó a = 4
Đáp án cần chọn là: D
Câu 16:
16/07/2024Tìm các hằng số a và b sao cho ( + ax + b) : (x + 1) dư 7 và ( + ax + b) : (x – 3) dư (-5)
Xem đáp án
Để + ax + b chia cho x + 1 dư 7 thì b – a – 1 = 7 ó -a + b = 8 (1)
Để + ax + b chia cho x – 3 dư -5 thì b + 3a + 27 = -5 ó 3a + b = -32 (2)
Từ (1) và (2) ta có hệ ó
Vậy a = -10, b = -2
Đáp án cần chọn là: C
Câu 17:
18/07/2024P = . Tìm n Є Z để P Є Z.
Xem đáp án
+ 3n – 1 = (2 – n + 2)(n – 1) + 1
Để + 3n – 1 chia hết cho n – 1 thì 1 chia hết cho n – 1
=> (n – 1) Є {1;-1}
n – 1 1 -1
n 2 0
P 9 1
TM TM
Vậy n Є {0; 2} để P Є Z
Đáp án cần chọn là: A
Câu 18:
16/07/2024Có bao nhiêu số nguyên x để giá trị của đa thức A = + 2x + 2 chia hết cho giá trị của đa thức B = + 1
Xem đáp án
Ta có A : B
Để giá trị của đa thức A = + 2x + 2 chia hết cho giá trị của đa thức B = + 1 thì
5 ⁝ ( + 1)
Hay ( + 1) Є U(5) = {-1; 1; -5; 5}
+) + 1 = -1 ó = -2 (VL)
+) + 1 = 1 ó = 0ó x = 0 (tm)
+) + 1 = -5 ó = -6 (VL)
+) + 1 = 5 ó = 4 ó x = ± 2 ™
Vậy có 3 giá trị của x thỏa mãn đề bài là x = 0; x = -2; x = 2
Đáp án cần chọn là: A