Trắc nghiệm Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp (có đáp án)
Trắc nghiệm Toán 8 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
-
368 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có
x2 – 6x + 8
= x2 – 4x – 2x + 8
= x(x – 4) – 2(x – 4)
= (x – 4)(x – 2)
Câu 2:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
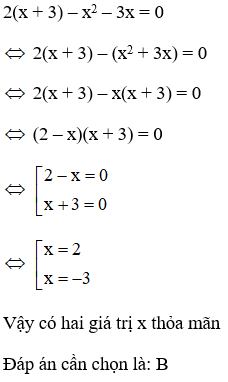
Câu 3:
23/07/2024Giá trị của biểu thức
A = x2 – 4y2 + 4x + 4
tại x = 62, y = -18 là
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có
A = x2 – 4y2 + 4x + 4
= (x2 + 4x + 4) – 4y2
= (x + 2)2 – (2y)2
= (x + 2 – 2y)(x + 2 + 2y)
Thay x = 62; y = -18 ta được
A = (62 + 2 – 2.(-18))(62 + 2 + 2.(-18))
= 100.28 = 2800
Câu 4:
22/07/2024Gọi x0 là giá trị thỏa mãn
x4 – 4x3 + 8x2 – 16x + 16 = 0. Chọn câu đúng
 Xem đáp án
Xem đáp án
Gọi x0 là giá trị thỏa mãn
x4 – 4x3 + 8x2 – 1
Đáp án: B
Giải thích:
Lời giải
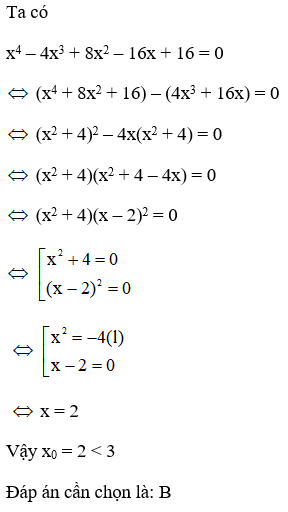
6x + 16 = 0. Chọn câu đúng
Câu 5:
23/07/2024Giá trị của biểu thức
B = x3 + x2y – xy2 – y3 tại x = 3,25 ; y = 6,75 là
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có
B = x3 + x2y – xy2 – y3
= x2(x + y) – y2(x + y)
= (x2 – y2)(x + y)
= (x – y)(x + y)(x + y)
= (x – y)(x + y)2
Thay x = 3,25 ; y = 6,75 ta được
B = (3,25 – 6,75)(3,25 + 6,75)2
= -3,5.102 = -350
Câu 6:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có
x2 – 7x + 10
= x2 – 2x – 5x + 10
= x(x – 2) – 5(x – 2)
= (x – 5)(x – 2)
Câu 7:
23/07/2024Cho biểu thức C = xyz – (xy + yz + zx) + x + y + z – 1.
Phân tích C thành nhân tử và tính giá trị của C khi x = 9; y = 10; z = 101.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có
C = xyz – (xy + yz + zx) + x + y + z – 1
= (xyz – xy) – (yz – y) – (zx – x) + (z – 1)
= xy(z – 1) – y(z – 1) – x(z – 1) + (z – 1)
= (z – 1)(xy – y – x + 1)
= (z – 1).[y(x – 1) – (x – 1)]
= (z – 1)(y – 1)(x – 1)
Với x = 9; y = 10; z = 101 ta có
C = (101 – 1)(10 – 1)(9 – 1)
= 100.9.8 = 7200
Câu 8:
23/07/2024Gọi x0 < 0 là giá trị thỏa mãn
x4 + 2x3 – 8x – 16 = 0. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
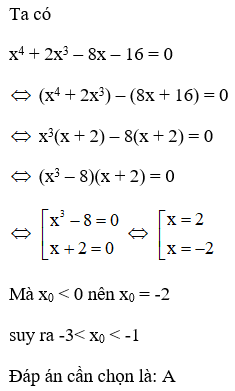
Câu 9:
23/07/2024Cho (x2 + x)2 + 4x2 + 4x – 12 = (x2 + x – 2)(x2 + x + …).
Điền vào dấu … số hạng thích hợp
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có
(x2 + x)2 + 4x2 + 4x – 12
= (x2 + x)2 + 4(x2 + x) – 12
Đặt t = x2 + x ta được
t2 + 4t – 12 = t2 + 6t – 2t – 12
= t(t + 6) – 2(t + 6)
= (t – 2)(t + 6)
= (x2 + x – 2)(x2 + x + 6)
Vậy số cần điền là 6.
Câu 10:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có
25 – a2 + 2ab – b2
= 25 – (a2 – 2ab + b2)
= 52 – (a – b)2
= (5 + a – b)(5 – a + b)
Câu 11:
18/07/2024Cho (x2 – 4x)2 + 8(x2 – 4x) + 15 = (x2 – 4x + 5)(x – 1)(x + …).
Điền vào dấu … số hạng thích hợp
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Đặt t = x2 – 4x ta được
t2 + 8t + 15
= t2 + 3t + 5t + 15
= t(t + 3) + 5(t + 3)
= (t + 5)(t + 3)
= (x2 – 4x + 5)(x2 – 4x + 3)
= (x2 – 4x + 5)(x2 – 3x – x + 3)
= (x2 – 4x + 5)(x(x – 3) – (x – 3))
= (x2 – 4x + 5)(x – 1)(x – 3)
Vậy số cần điền là -3
Câu 12:
21/07/2024Cho biểu thức D = a(b2 + c2) – b(c2 + a2) + c(a2 + b2) – 2abc.
Phân tích D thành nhân tử và tính giá trị của C khi a = 99; b = -9; c = 1.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có
D = a(b2 + c2) – b(c2 + a2) + c(a2 + b2) – 2abc
= ab2 + ac2 – bc2 – ba2 + ca2 + cb2 – 2abc
= (ab2 – a2b) + (ac2 – bc2) + (a2c – 2abc + b2c)
= ab(b – a) + c2(a – b) + c(a2 – 2ab + b2)
= -ab(a – b) + c2(a – b) + c(a – b)2
= (a – b)(-ab + c2 + c(a – b))
= (a – b)(-ab + c2 + ac – bc)
= (a – b)[(-ab + ac) + (c2 – bc)]
= (a – b)[a(c – b) + c(c – b)]
= (a – b)(a + c)(c – b)
Với a = 99; b = -9; c = 1, ta có
D = (99 – (-9))(99 + 1)(1 – (-9))
= 108.100.10 = 108000
Câu 13:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có x4 + 64
= (x2)2 + 16x2 + 64 – 16x2
= (x2)2 + 2.8.x + 82 – (4x)2
= (x2 + 8)2 – (4x)2
Câu 14:
18/07/2024Ta có (x + 2)(x + 3)(x + 4)(x + 5) – 24 = (x2 + 7x + a)(x2 + 7x + b)
với a, b là các số nguyên và a < b. Khi đó a – b bằng
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Ta có
T = (x + 2)(x + 3)(x + 4)(x + 5) – 24
= [(x + 2)(x + 5)].[(x + 3)(x + 4)] – 24
= (x2 + 7x + 10).(x2 + 7x + 12) – 24
Đặt x2 + 7x + 11= t, ta được
T = (t – 1)(t + 1) – 24
= t2 – 1 – 24 = t2 – 25
= (t – 5)(t + 5)
Thay t = x2 + 7x + 11, ta được
T = (t – 5)(t + 5)
= (x2 + 7x + 11 – 5)( x2 + 7x + 11 + 5)
= (x2 + 7x + 6)( x2 + 7x + 16)
Suy ra a = 6; b = 16
=> a – b = -10
Câu 15:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
m.n3 – 1 + m – n3
= (mn3 – n3) + (m -1)
= n3(m – 1) + (m – 1)
= (n3 + 1)(m - 1)
= (n + 1)(n2 – n + 1)(m – 1)
Câu 16:
21/07/2024Ta có (x – 1)(x – 2)(x + 4)(x + 5) – 27 = (x2 + 3x + a)(x2 + 3x + b)
với a, b là các số nguyên. Khi đó a + b bằng
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Gọi
T = (x – 1)(x – 2)(x + 4)(x + 5) – 27
= [(x – 1)(x + 4)].[(x – 2)(x + 5)] – 27
= (x2 + 3x – 4).(x2 + 3x – 10) – 27
Đặt x2 + 3x – 7 = t
=>
Từ đó ta có
T = (t – 3)(t + 3) – 27
= t2 – 9 – 27
= t2 – 36
= (t – 6)(t + 6)
Thay t = x2 + 3x – 7 ta được
T = (x2 + 3x – 7 – 6)( x2 + 3x – 7 + 6)
= (x2 + 3x – 13)( x2 + 3x – 1)
suy ra a = -13; b = -1
=> a + b = -14
Câu 17:
22/07/2024Cho (A): 16x4(x – y) – x + y = (2x – 1)(2x + 1)(4x + 1)2(x + y)
và (B): 2x3y – 2xy3 – 4xy2 – 2xy = 2xy(x + y – 1)(x – y + 1).
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có
(A): 16x4(x – y) – x + y
= 16x4(x – y) – (x – y)
= (16x4 – 1)(x – y)
= [(2x)4 – 1](x – y)
= [(2x)2 – 1][(2x)2 + 1](x – y)
= (2x – 1)(2x + 1)(4x2 + 1)(x – y)
Nên (A) sai
Và (B): 2x3y – 2xy3 – 4xy2 – 2xy
= 2xy(x2 – y2 – 2y – 1)
= 2xy[x2 – (y2 + 2y + 1)]
= 2xy[x2 – (y + 1)2]
= 2xy(x – y – 1)(x + y + 1).
Nên (B) sai.
Vậy cả (A) và (B) đều sai.
Câu 18:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
4x2 + 4x – y2 + 1
= ((2x)2 + 2.2x + 1) – y2
= (2x + 1)2 – y2
= (2x + 1 – y)(2x + 1 + y)
= (2x – y + 1)(2x + y + 1)
Vậy đa thức trong chỗ trống là 2x – y + 1
Câu 19:
18/07/2024Gọi x1; x2 là hai giá trị thỏa mãn 3x2 + 13x + 10 = 0.
Khi đó 2x1.x2 bằng
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
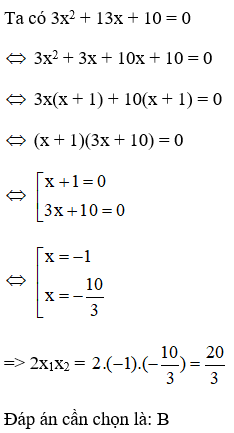
Có thể bạn quan tâm
- Trắc nghiệm Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp (có đáp án) (367 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Nhân đơn thức với đa thức (có đáp án) (1104 lượt thi)
- Bài tập: Phân tích đa thức thành nhân tử (có lời giải chi tiết) (826 lượt thi)
- Trắc nghiệm Những hằng đẳng thức đáng nhớ (có đáp án) (566 lượt thi)
- Bài tập Nhân đơn thức với đa thức (có lời giải chi tiết) (484 lượt thi)
- Trắc nghiệm Chia đơn thức cho đơn thức (có đáp án) (481 lượt thi)
- Bài tập Chia đa thức một biến đã sắp xếp (469 lượt thi)
- Trắc nghiệm Chia đa thức cho một biến đã sắp xếp (có đáp án) (407 lượt thi)
- Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung (có đáp án) (382 lượt thi)
- Trắc nghiệm Chia đa thức một biến đã sắp xếp có đáp án (Vận dụng) (358 lượt thi)
- Trắc nghiệm Chia đa thức cho đơn thức (có đáp án) (356 lượt thi)
