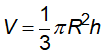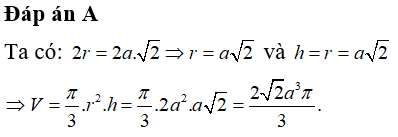52 câu trắc nghiệm: Khái niệm về mặt tròn xoay có đáp án
52 câu trắc nghiệm: Khái niệm về mặt tròn xoay có đáp án
-
449 lượt thi
-
104 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
13/07/2024Tam giác ABC vuông cân đỉnh A có cạnh huyền là a. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo thành hình nón (N). Diện tích xung quanh của hình nón (N) là:
 Xem đáp án
Xem đáp án
Đáp án C
Theo cách xây dựng hình nón ta có đường sinh của hình nón là: l = BC = a.
Bán kính đáy của hình nón là: r = AC = BC.sin45o = a/√2
Vậy ta có diện tích xung quanh của hình nón (N) là:
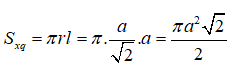
Câu 2:
13/07/2024Tam giác ABC vuông cân đỉnh A có cạnh huyền là a. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo thành hình nón (N). Diện tích xung quanh của hình nón (N) là:
 Xem đáp án
Xem đáp án
Đáp án C
Theo cách xây dựng hình nón ta có đường sinh của hình nón là: l = BC = a.
Bán kính đáy của hình nón là: r = AC = BC.sin45o = a/√2
Vậy ta có diện tích xung quanh của hình nón (N) là:
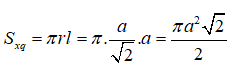
Câu 3:
13/07/2024Hình nón (N) có đường sinh gấp hai lần bán kính đáy. Góc ở đỉnh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án B
Từ giả thiết ta có l = 2r.
Gọi 2α là góc ở đỉnh của hình nón, khi đó ta có:
![]()
Vậy góc ở đỉnh của hình nón là 60o.
Câu 4:
18/07/2024Hình nón (N) có đường sinh gấp hai lần bán kính đáy. Góc ở đỉnh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án B
Từ giả thiết ta có l = 2r.
Gọi 2α là góc ở đỉnh của hình nón, khi đó ta có:
![]()
Vậy góc ở đỉnh của hình nón là 60o.
Câu 5:
20/07/2024Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón bằng:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
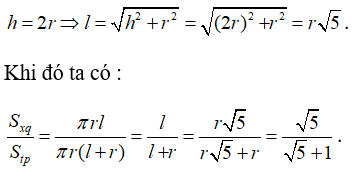
Câu 6:
13/07/2024Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón bằng:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
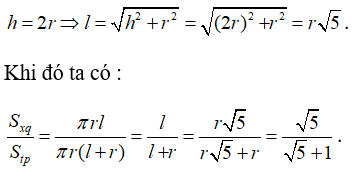
Câu 7:
18/07/2024Một chiếc phễu đựng dầu hình nón có chiều cao là 30cm và đường sinh là 50cm. Giả sử rằng lượng dầu mà chiếc phễu đựng được chính là thể tích của khối nón. Khi đó trong các lượng dầu sau đây, lượng dầu nào lớn nhất chiếc phễu có thể đựng được:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có h = 30cm; l = 50cm. Khi đó ta có
![]()
Thể tích khối nón là:
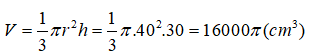
Câu 8:
13/07/2024Một chiếc phễu đựng dầu hình nón có chiều cao là 30cm và đường sinh là 50cm. Giả sử rằng lượng dầu mà chiếc phễu đựng được chính là thể tích của khối nón. Khi đó trong các lượng dầu sau đây, lượng dầu nào lớn nhất chiếc phễu có thể đựng được:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có h = 30cm; l = 50cm. Khi đó ta có
![]()
Thể tích khối nón là:
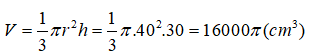
Câu 9:
14/07/2024Cho hình trụ có được khi quay hình chữ nhật ABCD quanh trục AB. Biết rằng AB = 2AD = 2a. Thể tích khối trụ đã cho theo a là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có h = AB = 2a, r = AD = a. Khi đó ta có thể tích khối trụ là: V = πr2h = 2πa3.
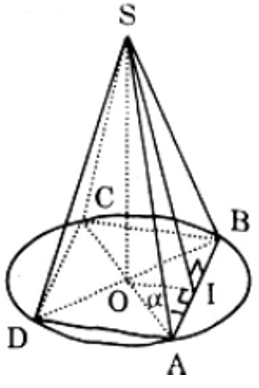
Câu 10:
13/07/2024Cho hình trụ có được khi quay hình chữ nhật ABCD quanh trục AB. Biết rằng AB = 2AD = 2a. Thể tích khối trụ đã cho theo a là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có h = AB = 2a, r = AD = a. Khi đó ta có thể tích khối trụ là: V = πr2h = 2πa3.
Câu 11:
15/07/2024Cho hình trụ có diện tích toàn phần là 7πa2 và bán kính đáy là a. Chiều cao của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
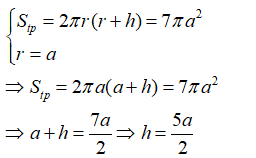
Câu 12:
15/07/2024Cho hình trụ có diện tích toàn phần là 7πa2 và bán kính đáy là a. Chiều cao của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
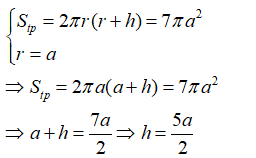
Câu 13:
23/07/2024Để làm một thùng phi hình trụ người ta cần hai miếng nhựa hình tròn làm hai đáy có diện tích mỗi hình là 4π(cm2) và một miếng nhựa hình chữ nhật có diện tích là 15π(cm2) để làm thân. Tính chiều cao của thùng phi được làm.
 Xem đáp án
Xem đáp án
Đáp án A
Diện tích miếng nhựa hình chữ nhật để làm thân bằng diện tích xung quanh của thùng phi.
Từ giả thiết ta có:
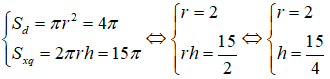
Câu 14:
18/07/2024Để làm một thùng phi hình trụ người ta cần hai miếng nhựa hình tròn làm hai đáy có diện tích mỗi hình là 4π(cm2) và một miếng nhựa hình chữ nhật có diện tích là 15π(cm2) để làm thân. Tính chiều cao của thùng phi được làm.
 Xem đáp án
Xem đáp án
Đáp án A
Diện tích miếng nhựa hình chữ nhật để làm thân bằng diện tích xung quanh của thùng phi.
Từ giả thiết ta có:
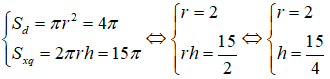
Câu 15:
19/07/2024Cho hình chữ nhật ABCD có AB = 2AD. Lần lượt quay hình chữ nhật quanh các trục AB, AD ta được hai khối trụ lần lượt gọi là (H1), (H2). Tính tỉ số thể tích của khối trụ (H1) chia cho thể tích của khối trụ (H2)
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có:
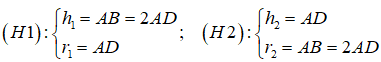
Khi đó ta có:
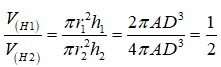
Câu 16:
17/07/2024Cho hình chữ nhật ABCD có AB = 2AD. Lần lượt quay hình chữ nhật quanh các trục AB, AD ta được hai khối trụ lần lượt gọi là (H1), (H2). Tính tỉ số thể tích của khối trụ (H1) chia cho thể tích của khối trụ (H2)
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có:
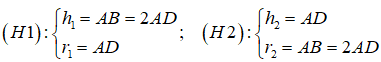
Khi đó ta có:
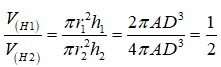
Câu 17:
15/07/2024Cho hình trụ có bán kính đáy bằng a và diện tích toàn phần 6πa2. Diện tích của thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua các trục của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có:
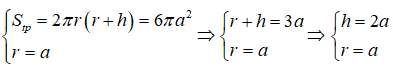
Thiết diện đã cho là một hình chữ nhật có các cạnh lần lượt là h và 2r. Khi đó ta có diện tích thiết diện là : S = 2rh = 4a2.
Câu 18:
23/07/2024Cho hình trụ có bán kính đáy bằng a và diện tích toàn phần 6πa2. Diện tích của thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua các trục của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có:
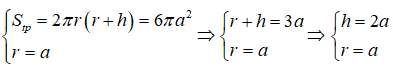
Thiết diện đã cho là một hình chữ nhật có các cạnh lần lượt là h và 2r. Khi đó ta có diện tích thiết diện là : S = 2rh = 4a2.
Câu 19:
13/07/2024Cho khối trụ có diện tích toàn phần là π và có thiết diện cắt bởi mặt phẳng đi qua trục là hình vuông. Thể tích khối trụ là:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
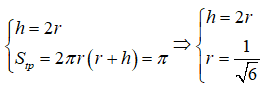
Thể tích khối trụ là:
V=πr2h=π.16.2√6=π3√6=π√618
Câu 20:
13/07/2024Cho khối trụ có diện tích toàn phần là π và có thiết diện cắt bởi mặt phẳng đi qua trục là hình vuông. Thể tích khối trụ là:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
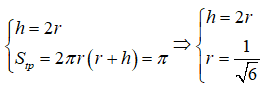
Thể tích khối trụ là:
V=πr2h=π.16.2√6=π3√6=π√618
Câu 25:
13/07/2024Cho khối nón tròn xoay có bán kính đáy r, đường sinh l và đường cao h. Công thức tính thể tích khối nón là:
 Xem đáp án
Xem đáp án
Đáp án C
Câu 26:
14/07/2024Cho khối nón tròn xoay có bán kính đáy r, đường sinh l và đường cao h. Công thức tính thể tích khối nón là:
 Xem đáp án
Xem đáp án
Đáp án C
Câu 27:
22/07/2024Hình nón (N) có đường sinh gấp hai lần đường cao. Góc ở đỉnh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Gọi 2α là góc ở đỉnh của hình nón. Từ giả thiết ta có:
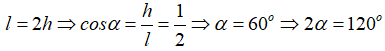
Câu 28:
13/07/2024Hình nón (N) có đường sinh gấp hai lần đường cao. Góc ở đỉnh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Gọi 2α là góc ở đỉnh của hình nón. Từ giả thiết ta có:
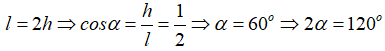
Câu 29:
13/07/2024Hình nón có chiều cao bằng 4/3 bán kính đáy. Tỉ số giữa diện tích toàn phần và diện tích xung quanh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có

Câu 30:
13/07/2024Hình nón có chiều cao bằng 4/3 bán kính đáy. Tỉ số giữa diện tích toàn phần và diện tích xung quanh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có

Câu 31:
23/07/2024Hình nón có góc ở đỉnh là 90o và có diện tích xung quanh là π√2. Độ dài đường cao của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Câu 32:
13/07/2024Hình nón có góc ở đỉnh là 90o và có diện tích xung quanh là π√2. Độ dài đường cao của hình nón là:

 Xem đáp án
Xem đáp án
Đáp án A
Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Câu 33:
13/07/2024Cho hình nón tròn xoay có đường cao h=15cm và bán kính đáy r = 20cm. Diện tích xung quanh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
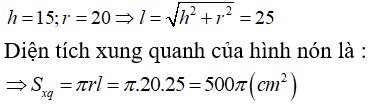
Câu 34:
22/07/2024Cho hình nón tròn xoay có đường cao h=15cm và bán kính đáy r = 20cm. Diện tích xung quanh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
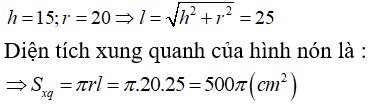
Câu 35:
13/07/2024Cho khối nón tròn xoay có đường cao h = 20cm và đường sinh l = 25cm. Thể tích khối nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
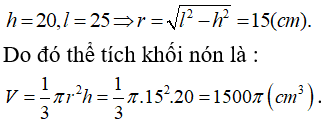
Câu 36:
17/07/2024Cho khối nón tròn xoay có đường cao h = 20cm và đường sinh l = 25cm. Thể tích khối nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
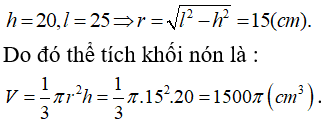
Câu 37:
18/07/2024Tam giác ABC vuông đỉnh A có AB = 2AC. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo ra hình nón (N1) và quay tam giác ABC quanh trục AC thì đoạn gấp khúc ABC tạo ra hình nón (N2). Tỉ số diện tích xung quanh của hình nón (N1) và diện tích xung quanh của hình nón (N2) là:
 Xem đáp án
Xem đáp án
Đáp án B
Đặt AC = a, ta có AB = 2a => BC = a√5. Khi đó ta có:
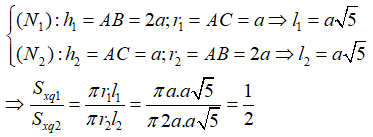
Câu 38:
14/07/2024Tam giác ABC vuông đỉnh A có AB = 2AC. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo ra hình nón (N1) và quay tam giác ABC quanh trục AC thì đoạn gấp khúc ABC tạo ra hình nón (N2). Tỉ số diện tích xung quanh của hình nón (N1) và diện tích xung quanh của hình nón (N2) là:
 Xem đáp án
Xem đáp án
Đáp án B
Đặt AC = a, ta có AB = 2a => BC = a√5. Khi đó ta có:
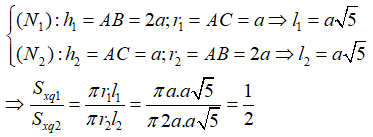
Câu 39:
19/07/2024Cho khối nón tròn xoay có góc ở đỉnh là 60o và đường sinh l = 6cm. Thể tích của khối nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
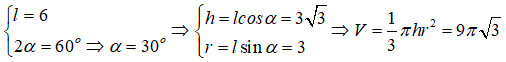
Câu 40:
20/07/2024Cho khối nón tròn xoay có góc ở đỉnh là 60o và đường sinh l = 6cm. Thể tích của khối nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
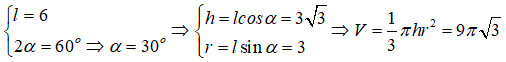
Câu 41:
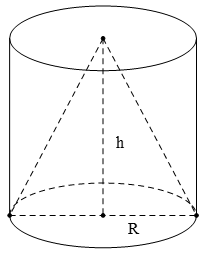
15/07/2024Cho một hình trụ có bán kính đáy R, chiều cao h và thể tích V1; một hình nón có đáy trùng với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích V2.
Khẳng định nào sau đây là khẳng định đúng ?
 Xem đáp án
Xem đáp án
Đáp án C
Hình trụ có bán kính đáy R và chiều cao h nên thể tích V1 = πR2h.
Hình nón có bán kính đáy R và chiều cao h nên thể tích V2 = 1/3 πR2h.
Từ đó suy ra V1 = 3V2.
Câu 42:
19/07/2024Cho một hình trụ có bán kính đáy R, chiều cao h và thể tích V1; một hình nón có đáy trùng với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích V2.
Khẳng định nào sau đây là khẳng định đúng ?

 Xem đáp án
Xem đáp án
Đáp án C
Hình trụ có bán kính đáy R và chiều cao h nên thể tích V1 = πR2h.
Hình nón có bán kính đáy R và chiều cao h nên thể tích V2 = 1/3 πR2h.
Từ đó suy ra V1 = 3V2.
Câu 43:
13/07/2024Khối nón có góc ở đỉnh là 60o và có thể tích là π. Độ dài đường sinh của khối nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
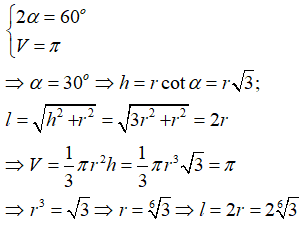
Câu 44:
17/07/2024Khối nón có góc ở đỉnh là 60o và có thể tích là π. Độ dài đường sinh của khối nón là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
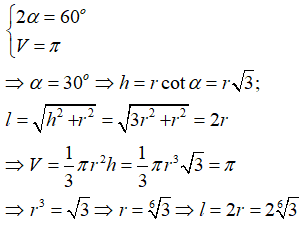
Câu 45:
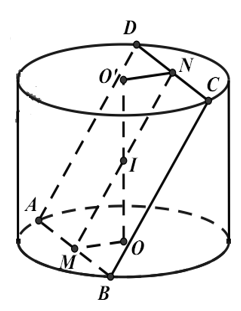
13/07/2024Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ.
 Xem đáp án
Xem đáp án
Đáp án D
Gọi M, N lần lượt là trung điểm AB và CD.
Khi đó OM ⊥ AB và O’N ⊥ CD
Gọi I là giao điểm của MN và OO’
Đặt R = OA và h = OO’. Khi đó ΔIOM vuông cân tại O nên:
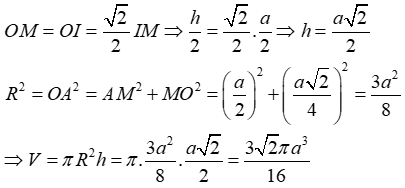
Câu 46:
20/07/2024Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ.

 Xem đáp án
Xem đáp án
Đáp án D
Gọi M, N lần lượt là trung điểm AB và CD.
Khi đó OM ⊥ AB và O’N ⊥ CD
Gọi I là giao điểm của MN và OO’
Đặt R = OA và h = OO’. Khi đó ΔIOM vuông cân tại O nên:
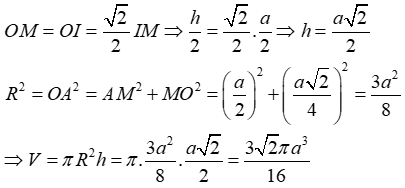
Câu 47:
13/07/2024Cho khối trụ có bán kính đáy 4m và đường cao là 5m. Thể tích khối trụ là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có: V = πr2h = π42.5 = 80π(m3)
Câu 48:
13/07/2024Cho khối trụ có bán kính đáy 4m và đường cao là 5m. Thể tích khối trụ là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có: V = πr2h = π42.5 = 80π(m3)
Câu 49:
13/07/2024Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có: AC = 2AD = 2a suy ra:
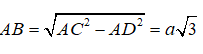
Khi đó ta có:
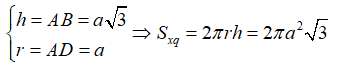
Câu 50:
13/07/2024Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết ta có: AC = 2AD = 2a suy ra:
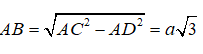
Khi đó ta có:
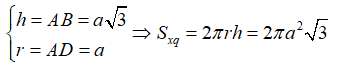
Câu 51:
13/07/2024Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm).

 Xem đáp án
Xem đáp án
Đáp án C
Gọi O, O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6π nên bán kính đáy của hình trụ là

Câu 52:
19/07/2024Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm).

 Xem đáp án
Xem đáp án
Đáp án C
Gọi O, O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6π nên bán kính đáy của hình trụ là

Câu 53:
15/07/2024Cho hình trụ có diện tích toàn phần 6πa2 và thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua trục là một hình vuông. Chiều cao của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án D
Vì thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua trục là một hình vuông nên: h = 2r
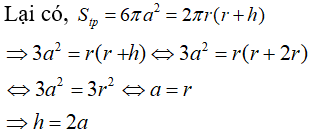
Câu 54:
13/07/2024Cho hình trụ có diện tích toàn phần 6πa2 và thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua trục là một hình vuông. Chiều cao của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án D
Vì thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua trục là một hình vuông nên: h = 2r
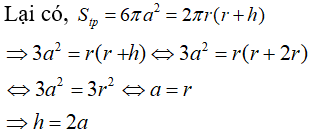
Câu 55:
13/07/2024Cho hình trụ có diện tích toàn phần là 12π, đường cao của hình trụ là 1. Diện tích xung quanh của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án B
Từ giả thiết ta có:
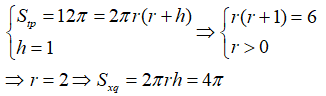
Câu 56:
15/07/2024Cho hình trụ có diện tích toàn phần là 12π, đường cao của hình trụ là 1. Diện tích xung quanh của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án B
Từ giả thiết ta có:
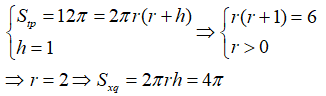
Câu 57:
23/07/2024Cho hình trụ có chiều cao bằng 2a và diện tích xung quanh là πa2. Bán kính đáy của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
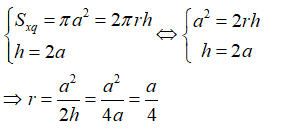
Câu 58:
16/07/2024Cho hình trụ có chiều cao bằng 2a và diện tích xung quanh là πa2. Bán kính đáy của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án D
Từ giả thiết ta có:
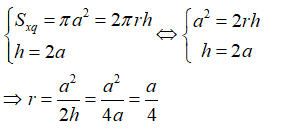
Câu 59:
17/07/2024Cho khối trụ có diện tích toàn phần 5πa2 và bán kính đáy là a. Thể tích khối trụ là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
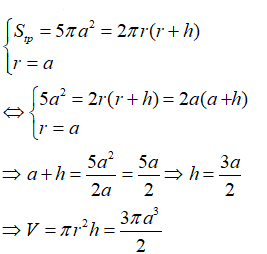
Câu 60:
13/07/2024Cho khối trụ có diện tích toàn phần 5πa2 và bán kính đáy là a. Thể tích khối trụ là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
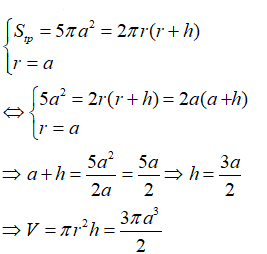
Câu 61:
15/07/2024Hình trụ (H) có diện tích toàn phần là 8π(cm2) và thể tích khối trụ là 3π(cm3). Tính chiều cao của hình trụ ta được bao nhiêu kết quả?
 Xem đáp án
Xem đáp án
Đáp án B
Từ giả thiết ta có:
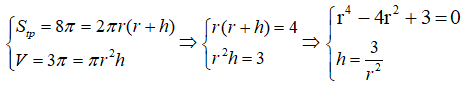
Do r > 0 nên ta có 2 giá trị r thỏa mãn hay có hai hình nón thỏa mãn đề bài
Câu 62:
13/07/2024Hình trụ (H) có diện tích toàn phần là 8π(cm2) và thể tích khối trụ là 3π(cm3). Tính chiều cao của hình trụ ta được bao nhiêu kết quả?
 Xem đáp án
Xem đáp án
Đáp án B
Từ giả thiết ta có:
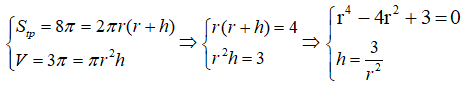
Do r > 0 nên ta có 2 giá trị r thỏa mãn hay có hai hình nón thỏa mãn đề bài
Câu 63:
17/07/2024Hình trụ (H) có tỉ số diện tích xung quanh và diện tích toàn phần là 1/3. Biết rằng thể tích khối trụ là 4π. Bán kính đáy của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
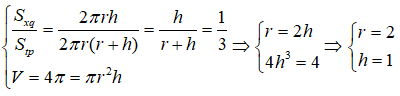
Câu 64:
13/07/2024Hình trụ (H) có tỉ số diện tích xung quanh và diện tích toàn phần là 1/3. Biết rằng thể tích khối trụ là 4π. Bán kính đáy của hình trụ là:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có:
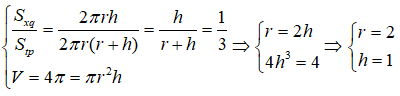
Câu 65:
13/07/2024Ta dùng hai hình chữ nhật có cùng kích cỡ để làm thành hai hình trụ (H1) và (H2) bằng cách quay các hình chữ nhật đó, lần lượt theo chiều dài và chiều rộng. Tỉ số hai diện tích xung quanh hình trụ (H1) và hình trụ (H2) là:
 Xem đáp án
Xem đáp án
Đáp án B
Gọi chiều dài và chiều rộng của hình chữ nhật là a và b.
Hình trụ (H1) có r1 = a ; h1 = b
Hình trụ (H2) có r2 = b ; h2= a
Ta có:
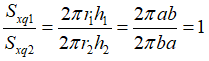
Câu 66:
22/07/2024Ta dùng hai hình chữ nhật có cùng kích cỡ để làm thành hai hình trụ (H1) và (H2) bằng cách quay các hình chữ nhật đó, lần lượt theo chiều dài và chiều rộng. Tỉ số hai diện tích xung quanh hình trụ (H1) và hình trụ (H2) là:
 Xem đáp án
Xem đáp án
Đáp án B
Gọi chiều dài và chiều rộng của hình chữ nhật là a và b.
Hình trụ (H1) có r1 = a ; h1 = b
Hình trụ (H2) có r2 = b ; h2= a
Ta có:
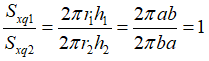
Câu 67:
17/07/2024Cho hình nón có đường cao h = 10cm và thiết diện cắt bởi mặt phẳng qua trục của hình nón là một tam giác đều. Diện tích xung quanh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án B
Từ giả thiết ta có thiết diện là tam giác đều cạnh 2r và đường cao h nên ta có:
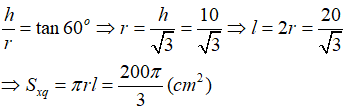
Câu 68:
23/07/2024Cho hình nón có đường cao h = 10cm và thiết diện cắt bởi mặt phẳng qua trục của hình nón là một tam giác đều. Diện tích xung quanh của hình nón là:
 Xem đáp án
Xem đáp án
Đáp án B
Từ giả thiết ta có thiết diện là tam giác đều cạnh 2r và đường cao h nên ta có:
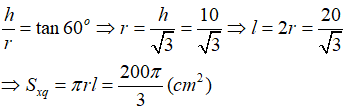
Câu 70:
03/11/2024Một hình nón có đường sinh bằng đường kính đáy. Diện tích xung quanh của hình nón bằng 9π. Tính đường cao h của hình nón.

 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải
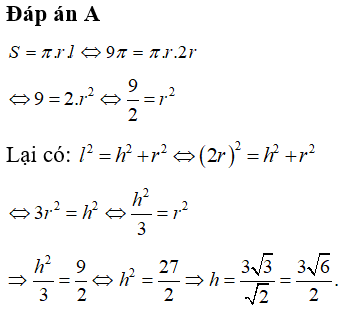
*Phương pháp giải
- Áp dụng công thức tính S xung quanh của hình nón: Sxq = pi.r.l
Thay dữ kiện đề bài cho vào để tính toán
*Lý thuyến cần nắm về hình nón:
Hình nón là hình được tạo ra khi quay tam giác vuông một vòng quanh một góc vuông cố định.
- Mặt đáy: là mặt phẳng có hình dạng hình chọn của hình nón.
- Đường cao: là khoảng cách từ tâm mặt đáy đến đỉnh của hình chóp hay được gọi là đường cao hạ từ đỉnh xuống tâm đáy hình nón. Được ký hiệu là: h.
- Đường sinh: là khoảng cách từ một điểm bất kỳ trên đường tròn đấy đến đỉnh của hình chóp. Được ký hiệu là: l.
- Bán kính đáy: là khoảng cách từ tâm đến một điểm trên hình tròn của mặt phẳng đáy. Được ký hiệu là: r.
1. Công thức tính diện tích đáy
- Đáy hình nón là hình tròn nên Sd=πr2
2. Công thức tính diện tích xung quanh hình nón
Cho hình nón có bán kính đáy r và độ dài đường sinh l.
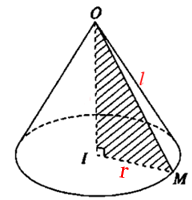
Khi đó:
Sxq = π.r.l
3. Công thức tính diện tích toàn phần hình nón
Cho hình nón có bán kính r, chiều cao h và đường sinh l
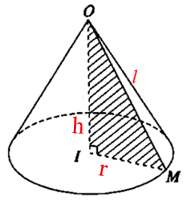
Diện tích toàn phần:
Stp=Sxq+Sd=πrl+πr2=πr(l+r)
Xem thêm các bài viết liên quan hay, chi tiết:
Công thức tính diện tích xung quanh, diện tích toàn phần hình nón (2024) chính xác nhất
50 bài toán về mặt nón và phương pháp giải bài tập (có đáp án 2024) – Toán 12
Câu 73:
21/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SC = a. Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
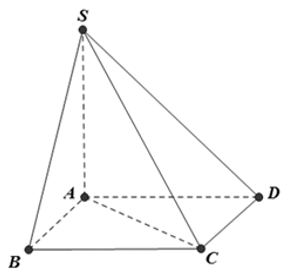
 Xem đáp án
Xem đáp án
Đáp án A
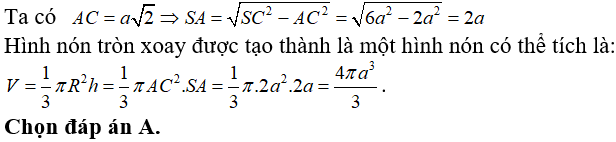
Câu 74:
22/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SC = a. Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:

 Xem đáp án
Xem đáp án
Đáp án A
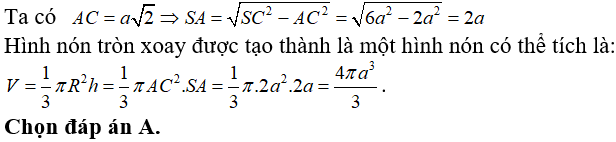
Câu 75:
17/07/2024Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = a, AB' = 2a. Diện tích toàn phần của hình trụ ngoại tiếp hình hộp là:
 Xem đáp án
Xem đáp án
Đáp án A
Xét tam giác vuông ABB’ ta có:
![]()
Hình trụ ngoại tiếp hình hộp đã cho có chiều cao h = AA’= BB’
Đáy hình trụ là đường tròn ngoại tiếp tứ giác ABCD và A’B’C’D’
Ta có:
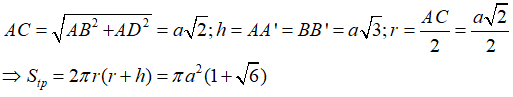
Câu 76:
23/07/2024Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = a, AB' = 2a. Diện tích toàn phần của hình trụ ngoại tiếp hình hộp là:
 Xem đáp án
Xem đáp án
Đáp án A
Xét tam giác vuông ABB’ ta có:
![]()
Hình trụ ngoại tiếp hình hộp đã cho có chiều cao h = AA’= BB’
Đáy hình trụ là đường tròn ngoại tiếp tứ giác ABCD và A’B’C’D’
Ta có:
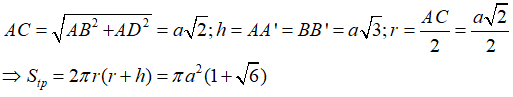
Câu 77:
11/10/2024Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và ![]() . Tính diện tích xung quanh hình nón ?
. Tính diện tích xung quanh hình nón ?
 Xem đáp án
Xem đáp án
Đáp án đúng: A
* Phương pháp giải:
Cho hình nón có bán kính đáy r và độ dài đường sinh l. Khi đó: Sxq = .r.l
* Lời giải:
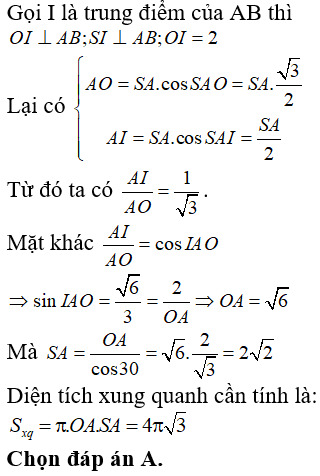
* Một số kiến thức cần nhớ về công thức tính diện tích hình nón:
Hình nón là hình được tạo ra khi quay tam giác vuông một vòng quanh một góc vuông cố định.

- Mặt đáy: là mặt phẳng có hình dạng hình chọn của hình nón.
- Đường cao: là khoảng cách từ tâm mặt đáy đến đỉnh của hình chóp hay được gọi là đường cao hạ từ đỉnh xuống tâm đáy hình nón. Được ký hiệu là: h.
- Đường sinh: là khoảng cách từ một điểm bất kỳ trên đường tròn đấy đến đỉnh của hình chóp. Được ký hiệu là: l.
- Bán kính đáy: là khoảng cách từ tâm đến một điểm trên hình tròn của mặt phẳng đáy. Được ký hiệu là: r.
- Diện tích xung quanh: Sxq = π.r.l
- Diện tích toàn phần:
- Thể tích hình nón bằng diện tích mặt đáy nhân với chiều cao: V = π.r2.h
Xem thêm các bài viết liên quan hay, chi tiết:
TOP 40 câu Trắc nghiệm Khái niệm về mặt tròn xoay (có đáp án 2024) - Toán 12
50 bài toán về mặt nón và phương pháp giải bài tập (có đáp án 2024) – Toán 12
Câu 78:
16/07/2024Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và ![]() . Tính diện tích xung quanh hình nón ?
. Tính diện tích xung quanh hình nón ?

 Xem đáp án
Xem đáp án
Đáp án A
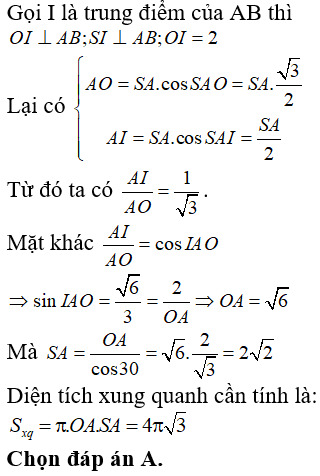
Câu 79:
13/07/2024Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc = 60°. Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:
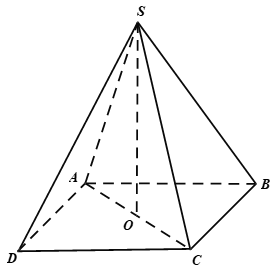
 Xem đáp án
Xem đáp án
Đáp án B

Câu 80:
22/07/2024Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc = 60°. Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:

 Xem đáp án
Xem đáp án
Đáp án B

Câu 81:
22/07/2024Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a, có diện tích xung quanh là:

 Xem đáp án
Xem đáp án
Đáp án C
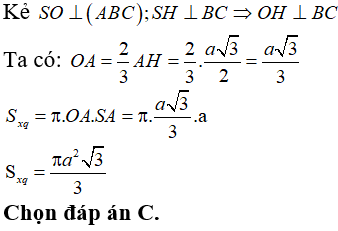
Câu 82:
21/07/2024Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a, có diện tích xung quanh là:

 Xem đáp án
Xem đáp án
Đáp án C
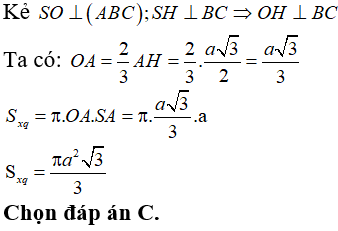
Câu 83:
04/01/2025Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng

 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải
Giả sử SAB là thiết diện qua trục của hình nón (như hình vẽ)
Tam giác SAB cân tại S và là tam giác cân nên SA = SB = a
Do đó:
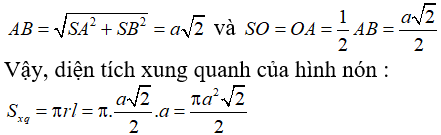
*Phương pháp giải
- Dựa vào tính chất tam giác vuông cân xác định chiều cao và bán kính đáy của hình nón.
- Khối nón có đường sinh là l, bán kính đáy có diện tích xung quanh: Sxq = πRl
*Lý thuyết cần nắm thêm về hình nón
Khi quay tam giác vuông AOC một vòng quanh cạnh OA cố định thì được một hình nón.
+ Điểm A được gọi đỉnh của hình nón.
+ Hình tròn (O) được gọi là đáy của hình nón.
+ Mỗi vị trí của AC được gọi là một đường sinh của hình nón.
+ Đoạn AO được gọi là đường cao của hình nón.
2. Diện tích – thể tích của hình nón
Đặt AC = l; l là đường sinh
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
+ Diện tích xung quanh: Sxq = πRl
+ Diện tích toàn phần: Stp = πRl + πR2
+ Thể tích:
Xem thêm một số bài viết liên quan hay, chi tiết:
Câu 84:
20/07/2024Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng

 Xem đáp án
Xem đáp án
Đáp án B
Giả sử SAB là thiết diện qua trục của hình nón (như hình vẽ)
Tam giác SAB cân tại S và là tam giác cân nên SA = SB = a
Do đó:
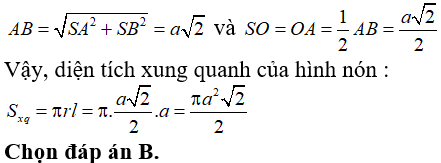
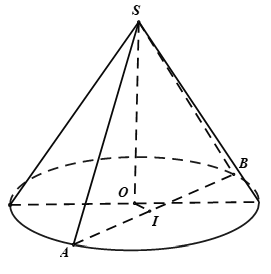
Câu 85:
23/07/2024Cho hình nón S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và ![]() . Tính diện tích xung quanh hình nón.
. Tính diện tích xung quanh hình nón.
 Xem đáp án
Xem đáp án
Đáp án D

Câu 86:
13/07/2024Cho hình nón S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và ![]() . Tính diện tích xung quanh hình nón.
. Tính diện tích xung quanh hình nón.

 Xem đáp án
Xem đáp án
Đáp án D

Câu 87:
20/07/2024Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng

 Xem đáp án
Xem đáp án
Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)

Câu 88:
21/07/2024Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng

 Xem đáp án
Xem đáp án
Đáp án A
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)

Câu 89:
13/07/2024Một người xây nhà phải xây bốn cái cột hình trụ cùng kích cỡ, bán kính đáy các cột là 25cm. Biết rằng tổng thể tích vật liệu (chính là tổng thể tích bốn khối trụ) là 3. Chiều cao của mỗi cột là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết đề bài ta có tổng thể tích của bốn khối trụ là 3 và bán kính đáy của mỗi khối trụ là r = 25cm = 0,25m.
Gọi h là chiều cao của các khối trụ ta có:
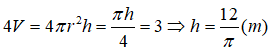
Câu 90:
22/07/2024Một người xây nhà phải xây bốn cái cột hình trụ cùng kích cỡ, bán kính đáy các cột là 25cm. Biết rằng tổng thể tích vật liệu (chính là tổng thể tích bốn khối trụ) là 3. Chiều cao của mỗi cột là:
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết đề bài ta có tổng thể tích của bốn khối trụ là 3 và bán kính đáy của mỗi khối trụ là r = 25cm = 0,25m.
Gọi h là chiều cao của các khối trụ ta có:
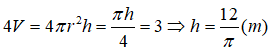
Câu 91:
14/07/2024Một hộp đứng bóng bàn hình trụ có chiều cao 30cm, bán kính 2,5cm. Vận động viên để các quả bóng bàn có bán kính 2,5cm vao hộp. Hỏi vận động viên có thể để được nhiều nhất bao nhiêu quả bóng bàn trong các kết quả sau?
 Xem đáp án
Xem đáp án
Đáp án B
Do bán kính của một quả bóng bàn hình cầu bằng bán kính hình trụ nên mỗi lần ta chỉ đặt được một quả bóng bàn vào hình trụ. Khi đó do mỗi quả bóng bàn chiếm chiều cao là 2,5x2=5cm nên với hình trụ cao 30cm thì đựng được nhiều nhất là 6 quả bóng bàn.
Câu 92:
20/07/2024Một hộp đứng bóng bàn hình trụ có chiều cao 30cm, bán kính 2,5cm. Vận động viên để các quả bóng bàn có bán kính 2,5cm vao hộp. Hỏi vận động viên có thể để được nhiều nhất bao nhiêu quả bóng bàn trong các kết quả sau?
 Xem đáp án
Xem đáp án
Đáp án B
Do bán kính của một quả bóng bàn hình cầu bằng bán kính hình trụ nên mỗi lần ta chỉ đặt được một quả bóng bàn vào hình trụ. Khi đó do mỗi quả bóng bàn chiếm chiều cao là 2,5x2=5cm nên với hình trụ cao 30cm thì đựng được nhiều nhất là 6 quả bóng bàn.
Câu 95:
23/07/2024Cho hình trụ có bán kính đáy 10cm và đường cao là 15cm. ta để một thước thẳng có chiều dài l vào trong hình trụ. Khi đó trong các kết quả sau l có thể nhận giá trị lớn nhất là:
 Xem đáp án
Xem đáp án
Đáp án B
Để một chiếc thước thẳng có thể nằm trong một hình trụ thì độ dài của nó không thể vượt quá được độ dài đường chéo của hình chữ nhật là thiết diện của hình trụ cắt bởi mặt phẳng qua trục của hình trụ. Do đó độ dài thước không vượt quá: ![]()
Câu 96:
20/07/2024Cho hình trụ có bán kính đáy 10cm và đường cao là 15cm. ta để một thước thẳng có chiều dài l vào trong hình trụ. Khi đó trong các kết quả sau l có thể nhận giá trị lớn nhất là:
 Xem đáp án
Xem đáp án
Đáp án B
Để một chiếc thước thẳng có thể nằm trong một hình trụ thì độ dài của nó không thể vượt quá được độ dài đường chéo của hình chữ nhật là thiết diện của hình trụ cắt bởi mặt phẳng qua trục của hình trụ. Do đó độ dài thước không vượt quá: ![]()
Câu 97:
13/07/2024Cho lăng trụ đứng ABCD.A'B'C'D có đáy ABCD là hình thang, AB = AD = a, CD = 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o. Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có hình thang ABCD là hình thang nội tiếp được đường tròn nên nó là hình thang cân AB = AD = BC = a
Khi đó tâm đường tròn ngoại tiếp hình thang ABCD là trung điểm I của CD và bán kính là r = a.
Ta có:
![]()
=> A'A = a = 3a => V = 3π
Câu 98:
20/07/2024Cho lăng trụ đứng ABCD.A'B'C'D có đáy ABCD là hình thang, AB = AD = a, CD = 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o. Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được:
 Xem đáp án
Xem đáp án
Đáp án A
Từ giả thiết ta có hình thang ABCD là hình thang nội tiếp được đường tròn nên nó là hình thang cân AB = AD = BC = a
Khi đó tâm đường tròn ngoại tiếp hình thang ABCD là trung điểm I của CD và bán kính là r = a.
Ta có:
![]()
=> A'A = a = 3a => V = 3π
Câu 99:
19/07/2024Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là:
 Xem đáp án
Xem đáp án
Đáp án D
Do AB // CD nên mặt phẳng (ABM) cắt mặt phẳng (SCD) theo một giao tuyến đi qua M và song song với CD, giao tuyến đó cắt SD tại N. Suy ra N là trung điểm của SD. Từ giả thiết ta có:
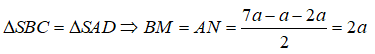
Áp dụng công thức đường trung tuyến trong tam giác SBC ta có:
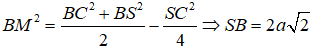
Khối nón đã cho có:
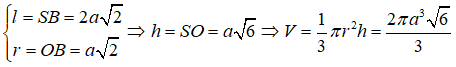
Câu 100:
19/07/2024Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là:
 Xem đáp án
Xem đáp án
Đáp án D
Do AB // CD nên mặt phẳng (ABM) cắt mặt phẳng (SCD) theo một giao tuyến đi qua M và song song với CD, giao tuyến đó cắt SD tại N. Suy ra N là trung điểm của SD. Từ giả thiết ta có:
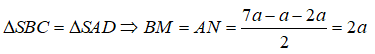
Áp dụng công thức đường trung tuyến trong tam giác SBC ta có:
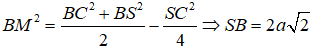
Khối nón đã cho có:
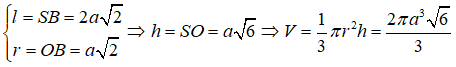
Câu 101:
23/07/2024Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h = và góc = α = 60°. Tính diện tích xung quanh của hình nón đỉnh S đáy là đường tròn ngoại tiếp tứ giác ABCD
 Xem đáp án
Xem đáp án
Đáp án A
Đặt r = OA, SO = h, SA = SB = SC = l là đường sinh của hình nón.
Gọi I là trung điểm của đoạn AB.
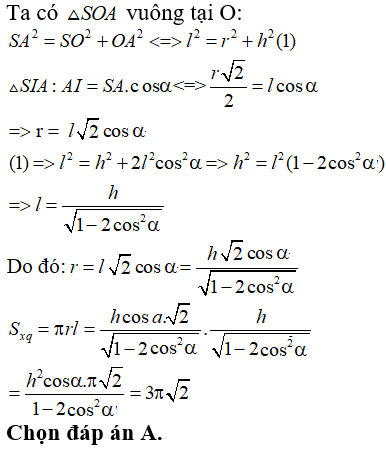
Câu 102:
23/07/2024Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h = và góc = α = 60°. Tính diện tích xung quanh của hình nón đỉnh S đáy là đường tròn ngoại tiếp tứ giác ABCD

 Xem đáp án
Xem đáp án
Đáp án A
Đặt r = OA, SO = h, SA = SB = SC = l là đường sinh của hình nón.
Gọi I là trung điểm của đoạn AB.
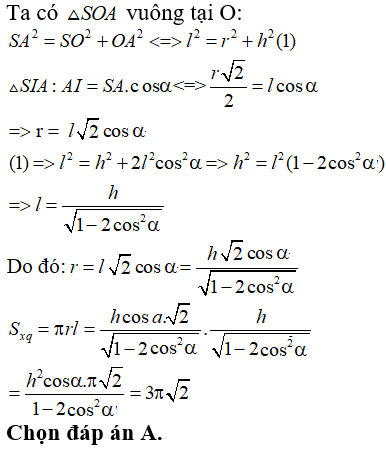
Câu 103:
16/07/2024Cho hình trụ có đường cao h và bán kính đáy là r. Trong các khối lăng trụ tứ giác nội tiếp hình trụ thì khối lăng trụ có thể tích lớn nhất bằng:
 Xem đáp án
Xem đáp án
Đáp án B
Gọi ABCD.A'B'C'D' là hình lăng trụ nội tiếp hình trụ. Khi đó lăng trụ đã cho là lăng trụ đứng và có chiều cao là chiều cao h của hình trụ. Vậy thể tích khối lăng trụ đạt giá trị lớn nhất khi và chỉ khi diện tích đáy ABCD đạt giá trị lớn nhất. Do ABCD nội tiếp đường tròn đáy của hình trụ nên ta có:
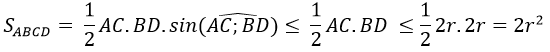
Dấu bằng xảy ra khi ABCD là hình vuông. Vậy thể tích khối lăng trụ tứ giác nội tiếp hình trụ lớn nhất là V = 2h
Câu 104:
14/07/2024Cho hình trụ có đường cao h và bán kính đáy là r. Trong các khối lăng trụ tứ giác nội tiếp hình trụ thì khối lăng trụ có thể tích lớn nhất bằng:
 Xem đáp án
Xem đáp án
Đáp án B
Gọi ABCD.A'B'C'D' là hình lăng trụ nội tiếp hình trụ. Khi đó lăng trụ đã cho là lăng trụ đứng và có chiều cao là chiều cao h của hình trụ. Vậy thể tích khối lăng trụ đạt giá trị lớn nhất khi và chỉ khi diện tích đáy ABCD đạt giá trị lớn nhất. Do ABCD nội tiếp đường tròn đáy của hình trụ nên ta có:
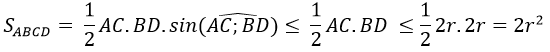
Dấu bằng xảy ra khi ABCD là hình vuông. Vậy thể tích khối lăng trụ tứ giác nội tiếp hình trụ lớn nhất là V = 2h
Có thể bạn quan tâm
- Trắc nghiệm Khái niệm về mặt tròn xoay (có đáp án) (544 lượt thi)
- 52 câu trắc nghiệm: Khái niệm về mặt tròn xoay có đáp án (448 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Nhận biết) (364 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Thông hiểu) (692 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Vận dụng - Phần 1) (317 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Nhận biết) (334 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Thông hiểu) (344 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Vận dụng) (381 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Phần 1) (321 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Mặt cầu (có đáp án) (458 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (Thông hiểu) (386 lượt thi)
- Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án (376 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (Vận dụng) (362 lượt thi)
- Trắc nghiệm Ôn tập Toán 12 Chương 2: Hình học (có đáp án) (340 lượt thi)
- Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án (Nhận biết) (339 lượt thi)
- 32 câu trắc nghiệm: Mặt cầu có đáp án (328 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (327 lượt thi)
- 20 câu trắc nghiệm: Ôn tập chương 2 Hình học 12 có đáp án (325 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (Nhận biết) (322 lượt thi)