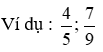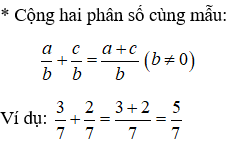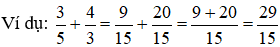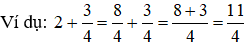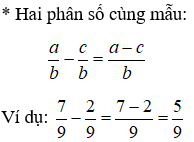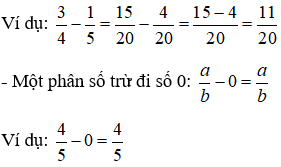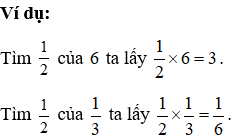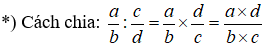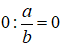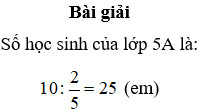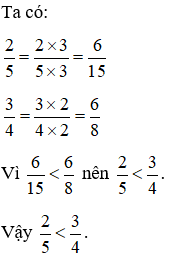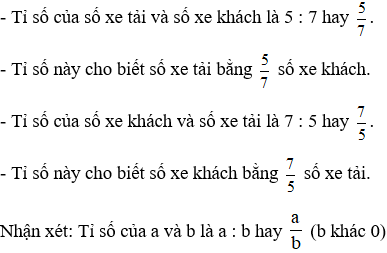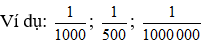Hệ thống kiến thức Toán lớp 4 Học kì 2

Hệ thống kiến thức Toán lớp 4 Học kì 2

PHÂN SỐ

1. Phân số là gì ?

Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.

2. Tính cơ bản của phân số

2.1. Khi ta cùng nhân hoặc cùng chia cả tử và mẫu số của một phân số với cùng một số tự nhiên

lớn hơn 1, ta được một phân số mới bằng phân số ban đầu.

2.2. Vận dụng tính chất cơ bản của phân số:

a. Rút gọn phân số

 (m > 1, a và b phải cùng chia hết cho m)

  được gọi là phân số tối giản khi c và d chỉ cùng chia hết cho 1 (hay c và d không cùng chia hết cho một số tự nhiên nào khác 1)

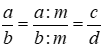
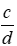
- Khi rút gọn phân số cần rút gọn đến phân số tối giản.

b. Quy đồng mẫu số - Quy đồng tử số:

PHÉP TÍNH VỚI PHÂN SỐ

1. Phép cộng phân số

* Hai phân số khác mẫu số:

- Quy đồng mẫu số 2 phân số rồi đưa về trường hợp cộng 2 phân số có cùng mẫu số.

* Cộng một số tự nhiên với một phân số.

- Viết số tự nhiên thành phân số có mẫu số bằng mẫu số của phân số đã cho.

- Cộng hai tử số và giữ nguyên mẫu số.

b. Tính chất cơ bản của phép cộng

2. Phép trừ phân số

* Hai phân số khác mẫu số: Quy đồng mẫu số 2 phân số rồi đưa về trường hợp trừ 2 phân số cùng mẫu số

3. Phép nhân phân số

- Muốn tìm giá trị phân số của một số ta lấy phân số nhân với số đó.

4. Phép chia phân số

- Số 0 chia cho một phân số: 

- Muốn tìm 1 số khi biết giá trị 1 phân số của nó ta lấy giá trị đó chia cho phân số tương ứng.

Ví dụ: Tìm số học sinh lớp 5A biết 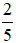 số học sinh của lớp 5A là 10 em.

SO SÁNH PHÂN SỐ

1. So sánh phân số bằng cách quy đồng mẫu số, quy đồng tử số

Bước 1: Quy đồng tử số

Bước 2: So sánh phân số đã quy đồng tử số

Ví dụ: So sánh hai phân số 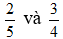 bằng cách quy đồng tử số

Hướng dẫn giải

2. So sánh phân số với phân số trung gian

Nếu hai phân số 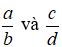  có a > c và b < d hoặc a < c và b < d (tử số của phân số này lớn hơn tử số của phân số kia đồng thời mẫu số của phân số này bé hơn mẫu số của phân số kia hoặc ngược lại) thì ta chọn phân số trung gian.

Khi chọn phân số trung gian ta có 2 cách chọn:

+ Cách 1: Chọn TS của phân số thứ nhất làm tử số của phân số trung gian và mẫu số của phân số thứ hai làm mẫu số của phân số trung gian.

+ Cách 2: Chọn tử số của phân số thứ hai làm TS của phân số trung gian và mẫu số của phân số thứ nhất làm MS của phân số trung gian.

3. So sánh phần bù

Nếu hai phân số 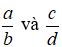  mà b - a = d - c (hiệu mẫu số và tử số của hai phân số bằng nhau) thì ta so sánh phần bù.

4.  So sánh phần thừa:

Nếu hai phân số 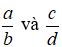  mà a - b = c - d (hiệu giữa tử số và mẫu số của hai phân số bằng nhau) thì ta so sánh phần thừa.

GIỚI THIỆU TỈ SỐ

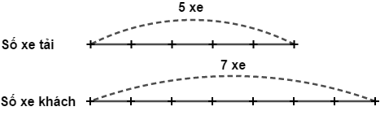
Ví dụ: Một đội xe có 5 xe tải và 7 xe khách

Ta nói:

Bài toán Tìm hai số khi biết tổng và tỉ số của hai số đó

*) Các bước giải

Bước 1: Xác định tổng, xác định tỉ số và biểu diễn tổng, tỉ trên sơ đồ đoạn thẳng tóm tắt bài toán.

Bước 2: Theo sơ đồ để tìm tổng số phần bằng nhau

Bước 3: Tìm giá trị một phần

Bước 4: Tìm số lớn (hoặc số bé)

Bước 5: Tìm số bé (hoặc số lớn) và ghi đáp số

*) Ví dụ:

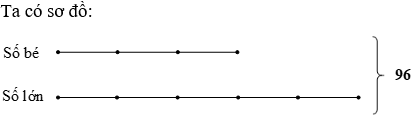
Tổng của hai số là 96. Tỉ số của hai số đó là 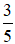. Tìm hai số đó.

Hướng dẫn giải

Tổng số phần bằng nhau là:

3 + 5 = 8 (phần)

Giá trị của một phần là:

96 : 8 = 12

Số bé là:

12 × 3 = 36

Số lớn là:

12 × 5 = 60

Đáp số: Số bé: 36, Số lớn: 60

Bài toán Tìm hai số khi biết hiệu và tỉ số của hai số đó.

*) Các bước giải

Bước 1: Xác định hiệu và tỉ của hai số đã cho trong đề bài và biểu thị trên sơ đồ đoạn thẳng tóm tắt bài toán.

Bước 2: Theo sơ đồ tìm hiệu số phần bằng nhau.

Bước 3: Tìm giá trị của một phần.

Bước 4: Tìm số bé ( hoặc số lớn).

Bước 5: Tìm số lớn (hoặc số bé) và đáp số.

*) Ví dụ

Hiệu của hai số là 24. Tỉ số của hai số đó là 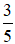. Tìm hai số đó.

Bài giải

Ta có sơ đồ:

Hiệu số phần bằng nhau là:

5 – 3 = 2 (phần)

Giá trị của một phần là:

24 : 2 = 12

Số bé là:

12 × 3 = 36

Số lớn là:

12 × 5 = 60

Đáp số: Số lớn 60; Số bé 36

TỈ LỆ BẢN ĐỒ

1) Tỉ lệ bản đồ là gì?

Tỉ lệ của bản đồ là tỉ số giữa một khoảng cách đo trên bản đồ và khoảng cách ngoài thực tế.

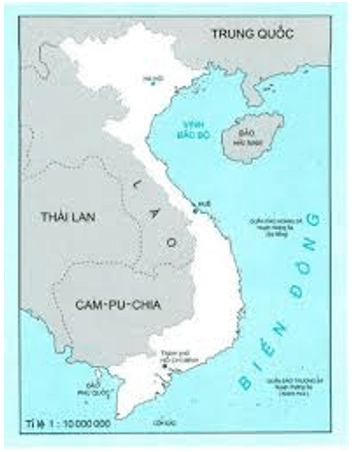
Ví dụ:

Ở góc dưới bản đồ của nước Việt Nam có ghi: Tỉ lệ 1 : 10 000 000. Tỉ lệ đó được gọi là tỉ lệ bản đồ.

Tỉ lệ 1 : 10 000 000 hay 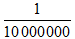 cho biết hình nước Việt Nam được vẽ thu nhỏ lại 10 000 000 lần. Chẳng hạn: Độ dài 1cm trên bản đồ ứng với độ dài thật là 10 000 000cm hay 100km.

Tỉ lệ bản đồ có thể được viết dưới dạng một phân số có tử số là 1.

2) Các dạng bài tập

2.1. Tính độ dài thật

Ví dụ. Trên bản đồ tỉ lệ 1: 1000000, quãng đường Hà Nội – Quảng Ninh đo được 112mm. Tìm độ dài thật của quãng đường Hà Nội – Quảng Ninh.

Bài giải

Quãng đường Hà Nội – Quảng Ninh dài là:

112 × 1000000 = 112 000 000 (mm)

Đổi: 112000000mm = 112km

Đáp số: 112km

2.2. Tính độ dài thu nhỏ trên bản đồ

Ví dụ. Quãng đường từ trung tâm Hà Nội đến Sơn Tây là 41km. Trên bản đồ tỉ lệ 1 : 1000000, quãng đường đó dài bài nhiêu mi-li-mét?

Bài giải

41km = 41000000mm

Trên bản đồ, quãng đường từ trung tâm Hà Nội đến Sơn Tây dài là:

41000000 : 1000000 = 41 (mm)

Đáp số: 41mm