Giải SBT Toán 10 trang 131 Tập 1 Chân trời sáng tạo

Giải SBT Toán 10 trang 131 Tập 1 Chân trời sáng tạo

Bài 1 trang 131 SBT Toán 10 Tập 1: Số quy tròn của 45,6534 với độ chính xác d = 0,01 là:

A. 45,65;

B. 45,6;

C. 45,7;

D. 45.

Lời giải:

Đáp án đúng là: C

Xét d = 0,01 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần trăm. Nên suy ra hàng lớn nhất của độ chính xác d = 0,01 là hàng phần trăm nên ta quy tròn số 45,6534 ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần mười.

Xét chữ số ở hàng phần trăm của 45,6534 là 5, nên ta suy ra được số quy tròn của 45,6534 đến hàng phần mười là 45,7.

Bài 2 trang 131 SBT Toán 10 Tập 1:

Cho biết $\sqrt[3]{3}=1,\mathrm{44224957....}$ Số gần đúng của $\sqrt[3]{3}$ với độ chính xác 0,0001 là:

A. 1,4422;

B. 1,4421;

C. 1,442;

D. 1,44.

Lời giải:

Đáp án đúng là: A

Xét d = 0,0001 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần chục nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,0001 là hàng phần chục nghìn nên ta quy tròn số $\sqrt[3]{3}$ ở hàng vừa tìm được, tức là hàng phần chục nghìn.

Xét chữ số ở hàng phần trăm nghìn của $\sqrt[3]{3}$ là 4, là số bé hơn 5 nên ta suy ra được số gần đúng của $\sqrt[3]{3}$ với độ chính xác d = 0,0001 là 1,4422.

Bài 3 trang 131 SBT Toán 10 Tập 1: Cho số gần đúng a = 0,1571. Số quy tròn của a với độ chính xác d = 0,002 là:

A. 0,16;

B. 0,15;

C. 0,157;

D. 0,159.

Lời giải:

Đáp án đúng là: A

Xét d = 0,002 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,002 là hàng phần nghìn nên ta quy tròn số a ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần trăm.

Xét chữ số ở hàng phần nghìn của a là 7, là số lớn hơn 5 nên ta suy ra được số quy tròn của a đến hàng phần trăm là 0,16.

Bài 4 trang 131 SBT Toán 10 Tập 1: Độ dài cạnh của một hình vuông là 8 ± 0,2 cm thì chu vi của hình vuông đó bằng:

A. 32 cm;

B. 32 ± 0,2 cm;

C. 64 ± 0,8 cm;

D. 32 ± 0,8 cm.

Lời giải:

Đáp án đúng là: D

Độ dài cạnh của một hình vuông là 8 ± 0,2 cm thì chu vi của hình vuông đó bằng: p = 4.(8 ± 0,2) = 32 ± 0,8 cm.

Bài 5 trang 131 SBT Toán 10 Tập 1: Trung vị của mẫu số liệu 4; 6; 7; 6; 5; 4; 5 là:

A. 4;

B. 5;

C. 6;

D. 7.

Lời giải:

Đáp án đúng là: B

Ta có: n = 7

Sắp xếp dãy số liệu theo thứ tự không giảm là: 4; 4; 5; 5; 6; 6; 7.

Vì n = 7 là số lẻ nên số trung vị của mẫu số liệu ở trên là: M_e = 5.

Bài 6 trang 131 SBT Toán 10 Tập 1: Khoảng biến thiên của mẫu số liệu 6; 7; 9; 4; 7; 5; 6; 6; 7; 9; 5; 6 là:

A. 3;

B. 4;

C. 5;

D. 6.

Lời giải:

Đáp án đúng là: C

Ta có: n = 12

Sắp xếp dãy số liệu theo thứ tự không giảm là:

4; 5; 5; 6; 6; 6; 6; 7; 7; 7; 9; 9

Khi đó, khoảng biến thiên R = 9 – 4 = 5.

Bài 7 trang 131 SBT Toán 10 Tập 1: Tứ phân vị thứ nhất của mẫu số liệu 2; 4; 5; 6; 6; 7; 3; 4 là:

A. 3;

B. 3,5;

C. 4;

D. 4,5.

Lời giải:

Đáp án đúng là: B

Ta có: n = 8

Sắp xếp dãy số liệu theo thứ tự không giảm là: 2; 3; 4; 4; 5; 6; 6; 7

Vì n = 8 là số chẵn nên ta có tứ phân vị thứ hai Q₂ = (4 + 5) : 2 = 4,5.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 2; 3; 4; 4.

Vậy Q₁ = (3 + 4) : 2 = 3,5.

Bài 8 trang 131 SBT Toán 10 Tập 1: Khoảng tứ phân vị của mẫu số liệu 4; 7; 5; 6; 6; 7; 9; 5; 6 là:

A. 1;

B. 1,5;

C. 2;

D. 2,5.

Lời giải:

Đáp án đúng là: C

Ta có: n = 9

Sắp xếp dãy số liệu theo thứ tự không giảm là: 4; 5; 5; 6; 6; 6; 7; 7; 9

Vì n = 9 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 6.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 4; 5; 5; 6.

Vậy Q₁ = (5 + 5) : 2 = 5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 6; 7; 7; 9.

Vậy Q₃ = (7 + 7) : 2 = 7.

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 7 – 5 = 2.

Bài 9 trang 131 SBT Toán 10 Tập 1: Dãy số liệu 5; 6; 0; 3; 5; 10; 3; 4 có các giá trị ngoại lệ là:

A. 0;

B. 10;

C. 0; 10;

D. ∅.

Lời giải:

Đáp án đúng là: B

Ta có: n = 8

Sắp xếp dãy số liệu theo thứ tự không giảm là: 0; 3; 3; 4; 5; 5; 6; 10

Vì n = 8 là số chẵn nên ta có tứ phân vị thứ hai Q₂ = (4 + 5) : 2 = 4,5.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 0; 3; 3; 4.

Vậy Q₁ = (3 + 3) : 2 = 3.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 5; 5; 6; 10.

Vậy Q₃ = (5 + 6) : 2 = 5,5.

Khi đó khoảng tứ phân vị là ∆_Q = Q₃ − Q₁ = 5,5 – 3 = 2,5.

Giá trị ngoại lệ x thỏa mãn

x > Q₃ + 1,5∆_Q = 5,5 + 1,5.2,5 = 9,25

Hoặc x < Q₁ − 1,5∆_Q = 3 − 1,5.2,5 = −0,75

Vậy đối chiếu mẫu số liệu suy ra giá trị ngoại lệ là 10.

Bài 10 trang 131 SBT Toán 10 Tập 1: Phương sai của dãy số liệu 4; 5; 0; 3; 3; 5; 6; 10 là:

A. 6,5;

B. 6,75;

C. 7;

D. 7,25.

Lời giải:

Đáp án đúng là: D

Ta có n = 8

Số trung bình của mẫu số liệu là

$$\begin{gathered} \overline{x}=\frac{4+5+0+3+3+5+6+10}{8} \\ =4,5. \end{gathered}$$

Khi đó phương sai của dãy số liệu là:

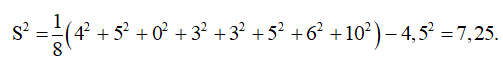
B. TỰ LUẬN

Bài 1 trang 131 SBT Toán 10 Tập 1: Viết số quy tròn của mỗi số sau với độ chính xác d:

a) a = −0,4356217 với d = 0,0001;

b) b = 0,2042 với d = 0,001.

Lời giải:

a) Xét d = 0,0001 ta thấy chữ số khác 0 đầu tiên bên trái của d nằm ở hàng  phần chục nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,0001 là hàng chục nghìn nên ta quy tròn số a ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần nghìn.

Xét chữ số ở hàng phần chục nghìn của a là 6, lớn hơn 5 nên ta suy ra được số quy tròn của a đến hàng phần nghìn là −0,436.

b) Xét d = 0,001 ta thấy, chữ số khác 0 đầu tiên bên trái của d nằm ở hàng phần nghìn. Nên suy ra hàng lớn nhất của độ chính xác d = 0,001 là hàng phần nghìn nên ta quy tròn số b ở hàng gấp 10 lần hàng vừa tìm được, tức là hàng phần trăm.

Xét chữ số ở hàng phần nghìn của b là 4, là số bé hơn 5 nên ta suy ra được số quy tròn của a đến hàng phần trăm là 0,20.

Bài 2 trang 131 SBT Toán 10 Tập 1: Tuấn đo được bán kính của một hình tròn là 5 ± 0,2 cm. Tuấn tính chu vi hình tròn là p = 31,4 cm. Hãy ước lượng sai số tuyệt đối của p, biết 3,141 < π < 3,142.

Lời giải:

Gọi $\overline{a}$ và $\overline{p}$ lần lượt là bán kính và chu vi của hình tròn.

Ta có $\overline{a}$ = 5 ± 0,2 nên suy ra 4,8 ≤ $\overline{a}$ ≤ 5,2.

Mà 3,141 < π < 3,142 nên suy ra:

2 . 4,8 . 3,141 ≤ 2.$\overline{a}$. π ≤ 2. 5,2 . 3,142

⇔ 30,1536 ≤ $\overline{p}$ ≤ 32,6768.

Ta có: p = 31,4 là số gần đúng của $\overline{p}$ nên sai số tuyệt đối của số gần đúng p là ∆_p = |$\overline{p}$ − 31,4|.

Mà 30,1536 ≤ $\overline{p}$ ≤ 32,6768

⇔ 30,1536 − 31,4 ≤ $\overline{p}$ − 31,4 ≤ 32,6768 − 31,4

⇔ −1,2464 ≤ $\overline{p}$ − 31,4 ≤ 1,2768

⇒ |$\overline{p}$ − 31,4| ≤ 1,2768.

Vậy suy ra sai số tuyệt đối của p là ∆_p = |$\overline{p}$ − 31,4| ≤ 1,2768.

Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Giải SBT Toán 10 trang 132 Tập 1