Nội dung bài viết

    Xem thêm

    Giải SBT Toán 10 trang 130 Tập 1 Chân trời sáng tạo

    Với Giải SBT Toán 10 trang 130 Tập 1 trong Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 130.

    1 190 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 trang 130 Tập 1 Chân trời sáng tạo

    Bài 4 trang 130 SBT Toán 10 Tập 1: Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn vị: °C).

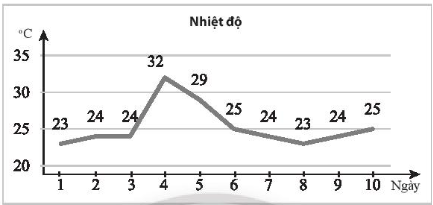
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    a) Hãy viết mẫu số liệu thống kê nhiệt độ từ biểu đồ trên.

    b) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.

    c) Hãy tìm phương sai và độ lệch chuẩn của mẫu số liệu đó.

    Lời giải:

    a) Ta có:

    +) Nhiệt độ đạt 23°C tại các ngày: 1 và 8

    +) Nhiệt độ đạt 24°C tại các ngày: 2, 3, 7 và 9

    +) Nhiệt độ đạt 25°C tại các ngày: 6 và 10

    +) Nhiệt độ đạt 29°C tại ngày: 5

    +) Nhiệt độ đạt 32°C tại ngày: 4

    Từ đó ta có mẫu số liệu thống kê nhiệt độ từ biểu đồ trên là

    23; 24; 24; 32; 29; 25; 24; 23; 24; 25

    b) Sắp xếp mẫu số liệu theo thứ tự không giảm:

    23; 23; 24; 24; 24; 24; 25; 25; 29; 32

    Khi đó, khoảng biến thiên R = 32 – 23 = 9.

    Vì n = 10 là số chẵn nên ta có tứ phân vị thứ hai

    Q2 = (24 + 24) : 2 = 24.

    Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q2, gồm Q2 vì n là số chẵn: 23; 23; 24; 24; 24.

    Vậy Q1 = 24.

    Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q2, gồm Q2 vì n là số chẵn: 24; 25; 25; 29; 32.

    Vậy Q3 = 25.

    Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 25 – 24 = 1.

    c) Số trung bình cộng:

    x¯=2.23+4.24+2.25+1.29+1.3210=25,3.

    Phương sai:

    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    = 7,61

    Khi đó độ lệch chuẩn S = S2=7,61≈2,76.

    Bài 5 trang 130 SBT Toán 10 Tập 1: Khuê và Trọng ghi lại số tin nhắn điện thoại mà mỗi người nhận được từ ngày 1/9 đến ngày 15/9 năm 2020 ở bảng sau:

    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    a) Hãy tìm phương sai của từng dãy số liệu.

    b) Sau khi bỏ đi các giá trị ngoại lệ (nếu có), hãy so sánh, số lượng tin nhắn mỗi bạn nhận được theo số trung bình và theo trung vị.

    Lời giải:

    a) n = 15

    +) Khuê:

    Số trung bình cộng:

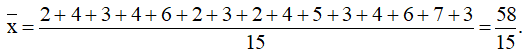
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    Phương sai:

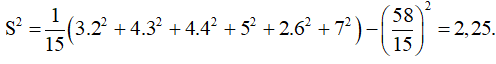
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    +) Trọng:

    Số trung bình cộng:

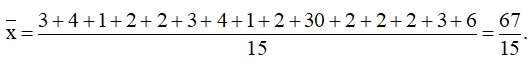
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    Phương sai:

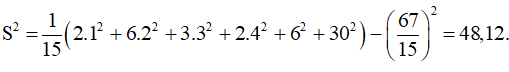
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    b)

    +) Khuê:

    Áp dụng các bước tìm tứ phân vị ta tìm được Q1 = 3, Q3 = 5

    Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 5 – 3 = 2.

    Giá trị ngoại lệ x thỏa mãn

    x > Q3 + 1,5∆Q = 5 + 1,5.2 = 8

    Hoặc x < Q1 − 1,5∆Q = 3 − 1,5.2 = 0

    Vậy đối chiếu mẫu số liệu của Khuê suy ra không có giá trị ngoại lệ.

    +) Trọng:

    Áp dụng các bước tìm tứ phân vị ta tìm được Q1 = 2, Q3 = 4

    Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 4 – 2 = 2.

    Giá trị ngoại lệ x thỏa mãn

    x > Q3 + 1,5∆Q = 4 + 1,5.2 = 7

    Hoặc x < Q1 − 1,5∆Q = 2 − 1,5.2 = −1

    Vậy đối chiếu mẫu số liệu của Trọng suy ra giá trị ngoại lệ là 30.

    Sau khi bỏ đi giá trị ngoại lệ thì giá trị trung bình của mẫu của Khuê là:

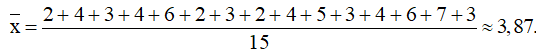
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    Và của Trọng là:

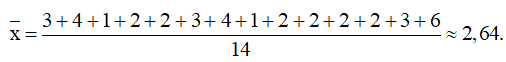
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    Khi đó trung vị của mẫu của Khuê là 4 (Với n = 15 là số lẻ)

    Và số trung vị của Trọng là (2 + 2) : 2 = 2 (Với n = 14 là số chẵn).

    Vậy so sánh theo cả số trung bình và số trung vị thì Khuê có nhiều tin nhắn mỗi ngày hơn Trọng.

    Bài 6 trang 130 SBT Toán 10 Tập 1: Bảng sau ghi giá bán ra lúc 11 giờ trưa của 2 mã cổ phiếu A và B trong 10 ngày liên tiếp (đơn vị: nghìn đồng).

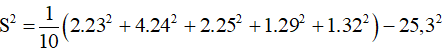
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    a) Biết có 1 trong 10 ngày trên có sự bất thường trong giá cổ phiếu. Hãy tìm ngày đó và giải thích.

    b) Sau khi bỏ đi ngày có giá bất thường, hãy cho biết giá cổ phiếu nào ổn định hơn. Tại sao?

    Lời giải:

    a) +) Mã cổ phiếu A:

    Áp dụng các bước tìm tứ phân vị ta tìm được Q1 = 45,1, Q3 = 45,5

    Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 45,5 – 45,1 = 0,4.

    Giá trị ngoại lệ x thỏa mãn

    x > Q3 + 1,5∆Q = 45,5 + 1,5.0,4 = 46,1

    Hoặc x < Q1 − 1,5∆Q = 45,1 − 1,5.0,4 = 44,5

    Vậy đối chiếu mẫu số liệu của A suy ra giá trị ngoại lệ là 35,5 và rơi vào ngày thứ 4.

    +) Mã cổ phiếu B:

    Áp dụng các bước tìm tứ phân vị ta dễ dàng tìm được Q1 = 47,8, Q3 = 49

    Khi đó khoảng tứ phân vị là ∆Q = Q3 − Q1 = 49 – 47,8 = 1,2.

    Giá trị ngoại lệ x thỏa mãn

    x > Q3 + 1,5∆Q = 49 + 1,5.1,2 = 50,8

    Hoặc x < Q1 − 1,5∆Q = 47,8 − 1,5.1,2 = 46

    Vậy đối chiếu mẫu số liệu của B suy ra giá trị ngoại lệ là 68,4 và rơi vào ngày thứ 4.

    b) Sau khi bỏ đi giá trị ngoại lệ thì giá trị trung bình của mẫu của A là:

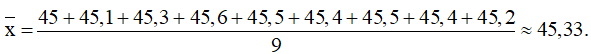
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    Khi đó phương sai của mẫu số liệu của A là

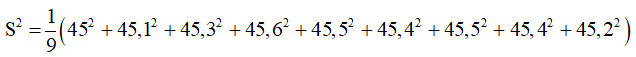    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)Và giá trị trung bình của mẫu của B là:

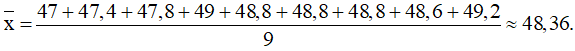
    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)

    Khi đó phương sai của mẫu số liệu của B là

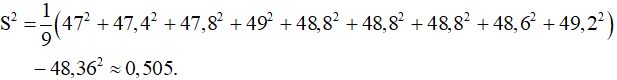    Sách bài tập Toán 10 Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu - Chân trời sáng tạo (ảnh 1)Vậy so sánh hai phương sai mẫu ta thấy 0,036 < 0,505 nên giá của mã cổ phiếu A ổn định hơn giá của mã cổ phiếu B.

    Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải SBT Toán 10 trang 129 Tập 1

    Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Bài 4: Tích vô hướng của hai vectơ

    Bài tập cuối chương 5

    Bài 1: Số gần đúng và sai số

    Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

    Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

    Xem thêm tài liệu Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Lý thuyết Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 190 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: