Giả sử năm đầu tiên, cô Hạnh gửi vào ngân hàng A (đồng) với lãi suất r%/năm

Giải Chuyên đề Toán 10 Cánh diều Bài 1: Phương pháp quy nạp toán học

Bài 10 trang 30 Chuyên đề Toán 10:

Giả sử năm đầu tiên, cô Hạnh gửi vào ngân hàng A (đồng) với lãi suất r%/năm. Hết năm đầu tiên, cô Hạnh không rút tiền ra và gửi thêm A (đồng) nữa. Hết năm thứ hai, cô Hạnh cũng không rút tiền ra và lại gửi thêm A (đồng) nữa. Cứ tiếp tục như vậy cho những năm sau. Chứng minh số tiền cả vốn lẫn lãi mà cô Hạnh có được sau n (năm) là $T_n=\frac{A(100+r)}{r}\left[{\left(1+\frac{r}{100}\right)}^n-1\right]$ (đồng), nếu trong khoảng thời gian này lãi suất không thay đổi.

Lời giải:

Xét mệnh đề P(x): "Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau n (năm) là $T_n=\frac{A(100+r)}{r}\left[{\left(1+\frac{r}{100}\right)}^n-1\right]$ (đồng) (n $\in$ ℕ^*)".

+) Khi n = 1:

Số tiền lãi người đó nhận được là: A . r% = $\frac{A.r}{100}$ (đồng).

Số tiền nhận được (bao gồm cả vốn lẫn lãi) là:

A + $\frac{A.r}{100}$

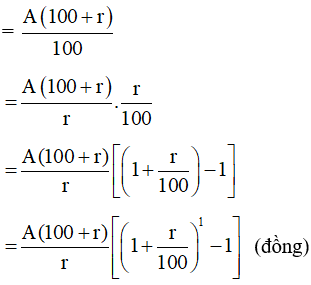
Vậy mệnh đề đúng với n = 1.

+) Với k là một số nguyên dương tuỳ ý mà mệnh đề đúng, ta phải chứng minh mệnh đề cũng đúng với k + 1, tức là: Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau (k +1) (năm) là $T_{k+1}=\frac{A(100+r)}{r}\left[{\left(1+\frac{r}{100}\right)}^{k+1}-1\right]$ (đồng).

Thật vậy, theo giả thiết quy nạp ta có:

Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau k (năm) là:

$T_k=\frac{A(100+r)}{r}\left[{\left(1+\frac{r}{100}\right)}^k-1\right]$ (đồng).

Vì cô Hạnh không rút tiền ra và lại gửi thêm A (đồng) nữa nên:

– Số tiền vốn của cô Hạnh sau (k + 1) năm là: T_k + A (đồng).

– Số tiền lãi cô Hạnh nhận được sau (k + 1) (năm) là:

(T_k + A) . r% (đồng).

– Số tiền cả vốn lẫn lãi mà cô Hạnh có được sau (k + 1) (năm) là:

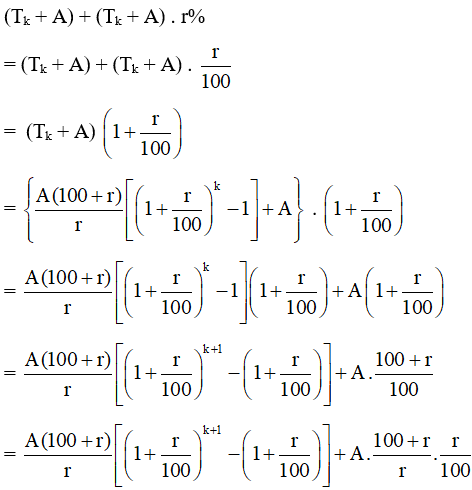
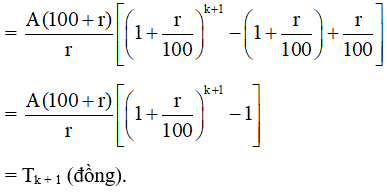
Vậy mệnh đề cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, mệnh đề đã cho đúng với mọi n $\in$ ℕ^*. Từ đó ta có điều phải chứng minh.

Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Cánh diều hay, chi tiết khác:

Hoạt động trang 23 Chuyên đề Toán 10: Xét mệnh đề chứa biến P(n) : "1 + 3 + 5 + ... + (2n – 1) = n²" với n là số nguyên dương...

Luyện tập 1 trang 25 Chuyên đề Toán 10: Chứng minh rằng với mọi n $\in$ ℕ^* ta có: Luyện tập 1 trang 25 Chuyên đề Toán 10...

Luyện tập 2 trang 26 Chuyên đề Toán 10: Chứng minh với mọi n $\in$ ℕ^*,${(1+\sqrt{2})}^n$, ${(1-\sqrt{2})}^n$ lần lượt viết được ở dạng...

Luyện tập 3 trang 26 Chuyên đề Toán 10: Chứng minh 16ⁿ – 15n – 1 chia hết cho 225 với mọi n $\in$ ℕ^*...

Bài 1 trang 29 Chuyên đề Toán 10: Cho S_n = 1 + 2 + 2² +... + 2ⁿ và T_n = 2^{n + 1} – 1, với n $\in$ ℕ^*...

Bài 2 trang 29 Chuyên đề Toán 10: Cho $S_n=1+\frac{1}{2}+\frac{1}{2^2}+\dots +\frac{1}{2^n}$...

Bài 3 trang 29 Chuyên đề Toán 10:  Cho $S_n=\frac{1}{1.5}+\frac{1}{5.9}+\frac{1}{9.13}+\dots$$+\frac{1}{(4n-3)(4n+1)}$...

Bài 4 trang 29 Chuyên đề Toán 10: Cho q là số thực khác 1. Chứng minh: 1 + q + q² +... + q^{n – 1} = $\frac{1-q^n}{1-q},$..

Bài 5 trang 29 Chuyên đề Toán 10: Chứng minh với mọi n $\in$ ℕ^*, ta có: a) 4ⁿ + 15n – 1 chia hết cho 9...

Bài 6 trang 29 Chuyên đề Toán 10: Chứng minh nⁿ > (n + 1)^{n – 1} với n $\in$ ℕ^*, n ≥ 2...

Bài 7 trang 29 Chuyên đề Toán 10: Chứng minh aⁿ – bⁿ = (a – b)(a^{n – 1} + a^{n – 2}b + ... + ab^{n –2} + b^{n – 1})...

Bài 8 trang 29 Chuyên đề Toán 10: Cho tam giác đều màu xanh (Hình thứ nhất). a) Nêu quy luật chọn tam giác đều...

Bài 9 trang 30 Chuyên đề Toán 10:  Quan sát Hình 6. a) Nêu quy luật sắp xếp các chấm đỏ...

Bài 11 trang 30 Chuyên đề Toán 10: Một người gửi số tiền A (đồng) vào ngân hàng. Biểu lãi suất của ngân hàng...

Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 2: Nhị thức newton

Bài 1: Elip

Bài 2: Hypebol

Bài 3: Parabol

Bài 4: Ba đường conic