Chuyên đề Toán 10 Bài 4 (Cánh diều): Ba đường conic

Giải bài tập Chuyên đề Toán 10 Bài 4: Ba đường conic

Giải bài tập trang 60, 66 Chuyên đề Toán 10 Bài 4

Hoạt động trang 60 Chuyên đề Toán 10:

Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.

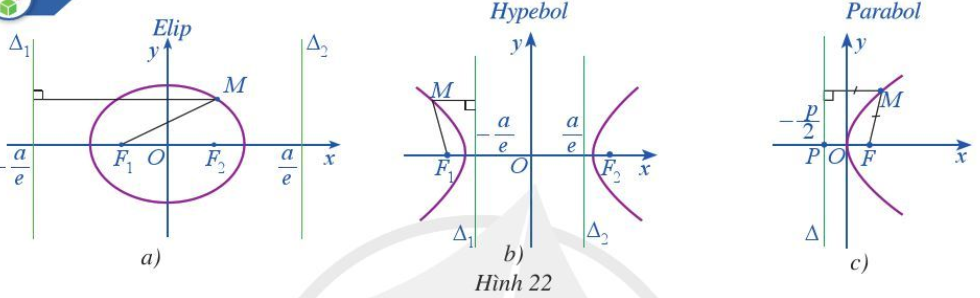
Lời giải:

- Với mọi điểm M thuộc elip (E): $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b >0), ta luôn có $\frac{MF}{d(M,\Delta )}=e$ (0 < e < 1), trong đó F là một trong hai tiêu điểm F₁, F₂ và Δ là đường chuẩn ứng với tiêu điểm F.

- Với mọi điểm M thuộc hypebol (H): $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0), ta luôn có $\frac{MF}{d(M,\Delta )}=e$ (e > 1), trong đó F là một trong hai tiêu điểm F₁, F₂ và Δ là đường chuẩn ứng với tiêu điểm F.

- Với mọi điểm M thuộc parabol (P): y² = 2px (p > 0), ta luôn có $\frac{MF}{d(M,\Delta )}=1$, trong đó F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm F.

Bài 1 trang 66 Chuyên đề Toán 10:

Cho hình chữ nhật ABCD với bốn đỉnh A(–4; 3), B(4; 3), C(4; –3), D(–4; –3).

a) Viết phương trình chính tắc của elip nhận ABCD là hình chữ nhật cơ sở. Vẽ elip đó.

b) Viết phương trình chính tắc của hypebol nhận ABCD là hình chữ nhật cơ sở. Vẽ hypebol đó.

Lời giải:

Gọi M, N lần lượt là trung điểm của AB, BC.

Toạ độ của M là

$$\begin{gathered} \left(x_M;y_M\right)=\left(\frac{x_A+x_B}{2};\frac{y_A+y_B}{2}\right) \\ =\left(\frac{-4+4}{2};\frac{3+3}{2}\right)=\left(0;3\right). \end{gathered}$$

Toạ độ của N là 

$$\begin{gathered} \left(x_N;y_N\right)=\left(\frac{x_B+x_C}{2};\frac{y_B+y_C}{2}\right) \\ =\left(\frac{4+4}{2};\frac{3+\left(-3\right)}{2}\right)=\left(4;0\right). \end{gathered}$$

a) Gọi phương trình chính tắc của elip cần tìm là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Vì ABCD là hình chữ nhật cơ sở của elip nên M, N là hai đỉnh của elip.

Lại có: M(0; 3) $\Rightarrow$ b = 3, N(4; 0) $\Rightarrow$ a = 4.

Vậy phương trình chính tắc của elip cần tìm là $\frac{x^2}{16}+\frac{y^2}{9}=1.$ 

+) Vẽ elip:

Ta thấy a = 4, b = 3. Toạ độ các đỉnh của elip là (–4; 0), (5; 0), (0; – 3), (0; 3).

Bước 1. Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng x = –4, x = 4, y = –3, y = 3.

Bước 2. Tìm một số điểm cụ thể thuộc elip, chẳng hạn ta thấy điểm $X\left(\frac{12}{5};\frac{12}{5}\right)$ và điểm $Y\left(\frac{16}{5};\frac{9}{5}\right)$ thuộc (E). Do đó các điểm $X_1\left(\frac{12}{5};-\frac{12}{5}\right),$ $X_2\left(-\frac{12}{5};\frac{12}{5}\right),$$X_3\left(-\frac{12}{5};-\frac{12}{5}\right)$, $Y_1\left(\frac{16}{5};-\frac{9}{5}\right),$ $Y_2\left(-\frac{16}{5};\frac{9}{5}\right),$$Y_3\left(-\frac{16}{5};-\frac{9}{5}\right)$ cũng thuộc $\left(E\right)$.

Bước 3. Vẽ đường elip (E) đi qua các điểm cụ thể trên, nằm ở phía trong hình chữ nhật cơ sở và tiếp xúc với các cạnh của hình chữ nhật cơ sở tại bốn đỉnh của (E) là
(–4; 0), (4; 0), (0; –3), (0; 3).

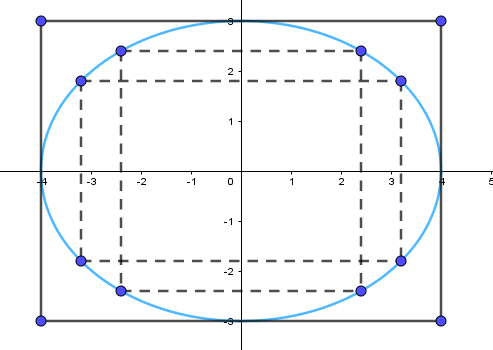
b)

Gọi phương trình chính tắc của hypebol cần tìm là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

Vì M(0; 3) và N(4;0) là trung điểm các cạnh của hình chữ nhật cơ sở nên a = 4, b = 3.

Vậy phương trình chính tắc của hypebol cần tìm là $\frac{x^2}{16}-\frac{y^2}{9}=1$ 

+) Vẽ hypebol:

Ta thấy a = 4, b = 3. (H) có các đỉnh là (–4; 0), (4; 0).

Bước 1. Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng x = –4, x = 4, y = –3, y = 3.

Bước 2. Vẽ hai đường chéo của hình chữ nhật cơ sở.

Tim một số điểm cụ thể thuộc hypebol, chẳng hạn ta thấy điểm $X\left(\frac{20}{3};4\right)$ thuộc (H). Do đó các điểm $X_1\left(\frac{20}{3};-4\right),X_2\left(-\frac{20}{3};4\right),X_3\left(-\frac{20}{3};-4\right)$ thuộc (H).

Bước 3. Vẽ đường hypebol bên ngoài hình chữ nhật cơ sở; nhánh bên trái tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm (–4; 0) và đi qua X₂, X₃; nhánh bên phải tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm (4; 0) và đi qua X, X₁. Vẽ các điểm thuộc hypebol càng xa gốc toạ độ thì càng sát với đường tiệm cận. Hypebol nhận gốc toạ độ là tâm đối xứng và hai trục toạ độ là hai trục đối xứng.

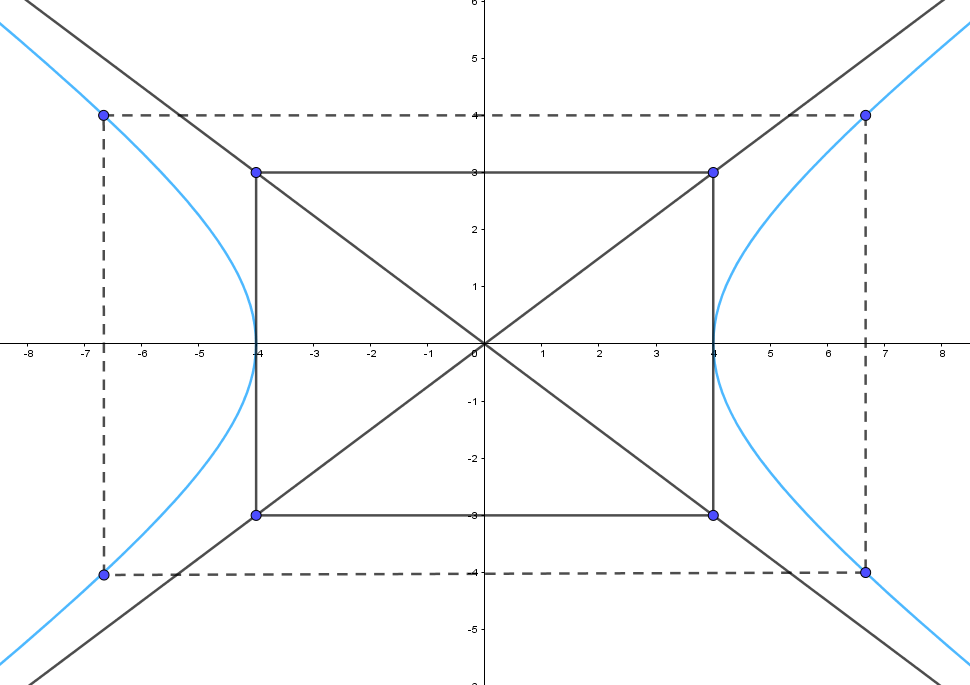
Giải bài tập trang 67 Chuyên đề Toán 10 Bài 4

Bài 2 trang 67 Chuyên đề Toán 10:

Các đường conic có phương trình như sau là đường elip hay hypebol? Tìm độ dài các trục, toạ độ tiêu điểm, tiêu cự, tâm sai của các đường conic đó.

a) $\frac{x^2}{100}+\frac{y^2}{64}=1$;

b) $\frac{x^2}{36}-\frac{y^2}{64}=1$.

Lời giải:

a) Đây là đường elip.

Ta có a = 10, b = 8 $\Rightarrow c=\sqrt{a^2-b^2}=6.$

Độ dài trục lớn là 2a = 20, độ dài trục bé là 2b = 16.

Toạ độ các tiêu điểm là F₁(–6; 0) và F₂(6; 0).

Tiêu cự là 2c = 12.

Tâm sai là $e=\frac{c}{a}=\frac{6}{10}=\frac{3}{5}.$

b) Đây là đường hypebol.

Ta có a = 6, b = 8 $\Rightarrow c=\sqrt{a^2+b^2}=10.$

Độ dài trục thực là 2a = 12, độ dài trục ảo là 2b = 16.

Toạ độ các tiêu điểm là F₁(–10; 0) và F₂(10; 0).

Tiêu cự là 2c = 20.

Tâm sai là $e=\frac{c}{a}=\frac{10}{6}=\frac{5}{3}.$

Bài 3 trang 67 Chuyên đề Toán 10:

Cho parabol có phương trình chính tắc y² = 2x. Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó.

Lời giải:

Ta có: 2p = 2 $\Rightarrow p=1\Rightarrow \frac{p}{2}=\frac{1}{2}.$

Vậy tiêu điểm của parabol là $F\left(\frac{1}{2};0\right)$ và đường chuẩn của parabol là $x=-\frac{1}{2}.$

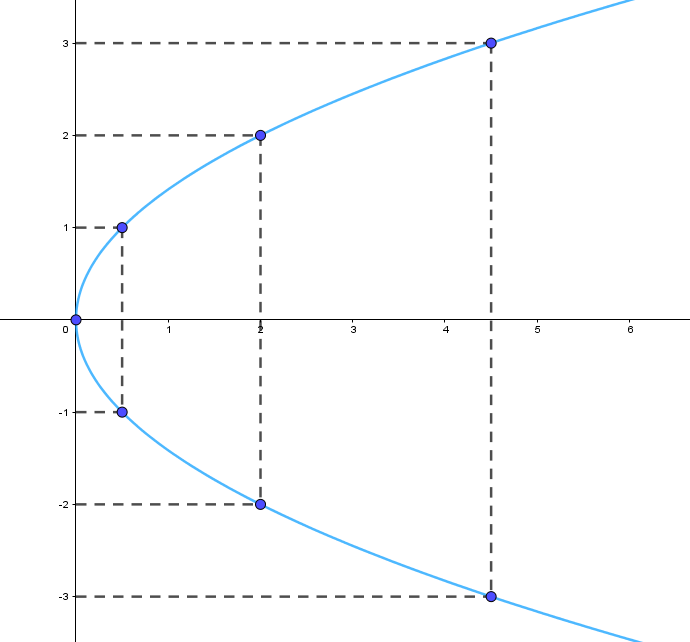
Vẽ parabol:

Bước 1. Lập bảng giá trị

Chú ý rằng ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau.

Bước 2. Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị.

Bước 3. Vẽ parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2.

Bài 4 trang 67 Chuyên đề Toán 10:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x = –5 và điểm F(–4; 0). Cho ba điểm A(–3; 1), B(2; 8), C(0; 3).

a) Tính các tỉ số sau: $\frac{AF}{d(A,\Delta )},\frac{BF}{d(B,\Delta )},\frac{CF}{d(C,\Delta )}$.

b) Hỏi mỗi điểm A, B, C lần lượt nằm trên loại đường conic nào nhận F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm đó?

Lời giải:

a) Ta viết lại phương trình đường thẳng Δ: x + 0 . y + 5 = 0. Khi đó:

$$\begin{gathered} \frac{AF}{d(A,\Delta )}=\frac{\sqrt{{\left(-4-\left(-3\right)\right)}^2+{\left(0-1\right)}^2}}{\frac{\left|-3+0.1+5\right|}{\sqrt{1^2+0^2}}} \\ =\frac{\sqrt{2}}{2}; \end{gathered}$$

$$\begin{gathered} \frac{BF}{d(B,\Delta )}=\frac{\sqrt{{\left(-4-2\right)}^2+{\left(0-8\right)}^2}}{\frac{\left|2+0.8+5\right|}{\sqrt{1^2+0^2}}} \\ =\frac{10}{7}; \end{gathered}$$

$$\begin{gathered} \frac{CF}{d(C,\Delta )}=\frac{\sqrt{{\left(-4-0\right)}^2+{\left(0-3\right)}^2}}{\frac{\left|0+0.3+5\right|}{\sqrt{1^2+0^2}}} \\ =1. \end{gathered}$$

b)

– Vì $\frac{AF}{d(A,\Delta )}=\frac{\sqrt{2}}{2}<1$ nên A nằm trên elip nhận F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm đó.

– Vì $\frac{BF}{d(B,\Delta )}=\frac{10}{7}>1$ nên A nằm trên hypebol nhận F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm đó.

– Vì $\frac{CF}{d(C,\Delta )}=1$ nên A nằm trên parabol nhận F là tiêu điểm và Δ là đường chuẩn.

Bài 5 trang 67 Chuyên đề Toán 10:

Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm (1 dặm xấp xỉ 1,609 km). Tìm tâm sai của quỹ đạo đó, biết bán kính của Trái Đất xấp xỉ 4000 dặm. (Nguồn: Sách giáo khoa Hình học 10, Ban Nâng cao, Nhà xuất bản Giảo dục Việt Nam, 2018)

Lời giải:

Chọn hệ trục toạ độ sao cho tâm Trái Đất trùng với tiêu điểm F₁ của elip.

Khi đó elip có phương trình là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Theo đề bài, ta có: vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm, mà bán kính của Trái Đất xấp xỉ 4000 dặm nên vệ tinh cách tâm Trái Đất gần nhất là 583 + 4000 = 4583 dặm và xa nhất là 1342 + 4000 = 5342 dặm.

Giả sử vệ tinh có toạ độ là M(x; y).

Khi đó khoảng cách từ vệ tinh đến tâm Trái Đất là: MF₁ = a + $\frac{c}{a}$x.

Vì –a ≤ x ≤ a nên a – c ≤ MF₁ ≤ a + c.

Vậy khoảng cách nhỏ nhất và lớn nhất từ vệ tinh đến tâm Trái Đất lần lượt là a – c và a + c.

$$\begin{gathered} \Rightarrow \left\{\begin{array}{l}a-c=4583\\ a+c=5342\end{array}\right.\Rightarrow \left\{\begin{array}{l}a=4962,5\\ c=379,5\end{array}\right. \\ \Rightarrow e=\frac{c}{a}=\frac{379,5}{4962,5}\approx 0,076. \end{gathered}$$

Vậy tâm sai của quỹ đạo này xấp xỉ 0,076.

Bài 6 trang 67 Chuyên đề Toán 10:

Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có một trong hai tiêu điểm là tâm của Mặt Trời. Biết elip này có bán trục lớn a ≈ 5,906 . 10⁶ km và tâm sai e ≈ 0,249. (Nguồn: https://vi.wikipedia.org)

Tìm khoảng cách nhỏ nhất (gần đúng) giữa Sao Diêm Vương và Mặt Trời.

Lời giải:

Chọn hệ trục toạ độ sao cho Mặt Trời trùng với tiêu điểm F₁ của elip.

Khi đó elip có phương trình là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Theo đề bài, ta có: elip này có bán trục lớn a ≈ 5,906 . 10⁶ km và tâm sai e ≈ 0,249

Giả sử Sao Diêm Vương có toạ độ là M(x; y).

Khi đó khoảng cách giữa Sao Diêm Vương và Mặt Trời là: MF₁ = a + ex.

Vì x ≥ –a nên MF₁ ≥ a – ea ≈ 5,906 . 10⁶ – 0,249 . 5,906 . 10⁶ = 4435406 (km).

Vậy khoảng cách nhỏ nhất giữa Sao Diêm Vương và Mặt Trời xấp xỉ 4435406 km.

Bài 7 trang 67 Chuyên đề Toán 10:

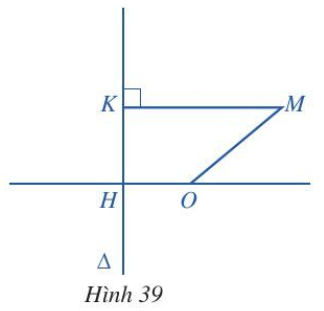
Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).

Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Chứng minh tập hợp các điểm M trong mặt phẳng sao cho MK² – MO² = 1 là một đường parabol.

Lời giải:

Chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH.

Giả sử M có toạ độ (x; y) thì K có toạ độ là (–1; y).

Khi đó:

MK² – MO² = 1

$\iff${[x – (–1)]² + (y – y)²} – [(0 – x)² + (0 – y)²] = 1

$\iff${(x + 1)² + 0²} – [x² + y²] = 1

$\iff$(x² + 2x +1) – (x² + y²) = 1

$\iff$2x +1 – y² = 1

$\iff$ y² = 2x.

Vậy tập hợp các điểm M là parabol có phương trình y² = 2x.

Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 1: Phương pháp quy nạp toán học

Bài 2: Nhị thức newton

Bài 1: Elip

Bài 2: Hypebol

Bài 3: Parabol