Câu hỏi:
18/07/2024 248Xét tính đồng biến và nghịch biến của hàm số y=f(x)=-x2+4x-2 trên các khoảng (-∞;2) và (2;+∞).
A. f(x) đồng biến trên khoảng (-∞;2) và nghịch biến trên khoảng (2;+∞)
B. f(x) đồng biến trên cả hai khoảng (-∞;2) và (2;+∞)
C. f(x) nghịch biến trên khoảng (-∞;2) và đồng biến trên khoảng (2;+∞)
D. f(x) nghịch biến trên cả hai khoảng (-∞;2) và (2;+∞)
Trả lời:
Giải bởi Vietjack
Với x1≠x2 ta có:
f(x2)-f(x1)x2-x1=(-x22+4x2-2)-(-x12+4x1-2)x2-x1=-(x22-x12)+4(x2-x1)x2-x1=-(x2+x1)+4.
· Với x1,x2∈(-∞;2) thì x1 < 2; x2 <2 nên x1+x2<4⇒-(x1+x2)+4>0 nên f(x) đồng biến trên khoảng (-∞;2).
· · Với x1,x2∈(2;+∞) thì x1>2; x2 >2 nên x1+x2>4⇒-(x1+x2)+4<0 nên f(x) nghịch biến trên khoảng (2;+∞).
Vậy đáp án là A.
Nhận xét: Với 4 phương án trả lời cho ta biết f(x) đồng biến hoặc nghịch biến trên mỗi khoảng (-∞;2) và (2;+∞).
Vì vậy, ta lấy hai giá trị bất kì x1<x2 thuộc mỗi khoảng rồi so sánh f(x1) và f(x2). Chẳng hạn x1=0;x2=1 có f(0)=-2 ;f(1)=1 nên f(0)<f(1), suy ra f(x) đồng biến trên khoảng (-∞;2).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 6:
Trong các điểm M( -1; 5); N(1; 4); P(2; 0); Q(3; 1), điểm nào thuộc đồ thị hàm số y=x2-2x+5
Câu 10:
Cho hàm số y=f(x) có đồ thị như hình vẽ bên.
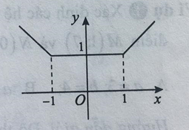
Khẳng định nào sau đây là đúng?
Câu 15:
Tìm m để hàm số y=mx+2 luôn nghịch biến trong khoảng xác định của nó.
