Câu hỏi:
15/11/2024 2,079
Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
A. I(– 4; – 4);
B. I(– 1; – 1);
B. I(– 1; – 1);
C. I(– 4; 4);
C. I(– 4; 4);
D. I(4; 4).
D. I(4; 4).
Trả lời:
Giải bởi Vietjack
Đáp án đúng là : A
Lời giải:
Tọa độ đỉnh \[I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\]
Ta có \[ - \frac{b}{{2a}} = - \frac{8}{{2.1}} = - 4\]; \[ - \frac{\Delta }{{4a}} = - \frac{{{8^2} - 4.1.12}}{{4.1}} = - 4\]
Vậy tọa độ đỉnh I(– 4; – 4)
*Phương pháp giải:
Cho parabol (P): y = ax2 + bx + c, ta có:
- Tọa độ đỉnh I của Parabol là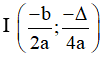 
(trong đó Δ = b2 - 4ac)
*Lý thuyết:
- Khái niệm đường parabol: Một đường parabol là một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
- Phương trình Parabol có dạng: y = ax2 + bx + c
- Gọi I là đỉnh của Parabol ta có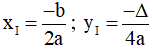 
( trong đó Δ = b2 - 4ac )
- Phương trình hoành độ giao điểm của hai đồ thị hàm số y = f(x) và y = g(x) là: f(x) = g(x).
- Gốc tọa độ có tọa độ là O(0; 0)
- Trục tung có phương trình: x = 0.
- Trục hoành có phương trình: y = 0
Xem thêm
Lý thuyết Hàm số bậc hai – Toán 10 Chân trời sáng tạo
Đáp án đúng là : A
Lời giải:
Tọa độ đỉnh \[I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\]
Ta có \[ - \frac{b}{{2a}} = - \frac{8}{{2.1}} = - 4\]; \[ - \frac{\Delta }{{4a}} = - \frac{{{8^2} - 4.1.12}}{{4.1}} = - 4\]
Vậy tọa độ đỉnh I(– 4; – 4)
*Phương pháp giải:
Cho parabol (P): y = ax2 + bx + c, ta có:
- Tọa độ đỉnh I của Parabol là 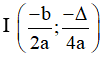(trong đó Δ = b2 - 4ac)
*Lý thuyết:
- Khái niệm đường parabol: Một đường parabol là một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
- Phương trình Parabol có dạng: y = ax2 + bx + c
- Gọi I là đỉnh của Parabol ta có 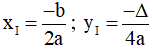( trong đó Δ = b2 - 4ac )
- Phương trình hoành độ giao điểm của hai đồ thị hàm số y = f(x) và y = g(x) là: f(x) = g(x).
- Gốc tọa độ có tọa độ là O(0; 0)
- Trục tung có phương trình: x = 0.
- Trục hoành có phương trình: y = 0
Xem thêm
Lý thuyết Hàm số bậc hai – Toán 10 Chân trời sáng tạo
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ ℝ.
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x ∈ ℝ.
Câu 3:
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
Câu 4:
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
Cho f(x) = x2 – 1. Tìm khẳng định sai trong các khẳng định sau đây
Câu 6:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
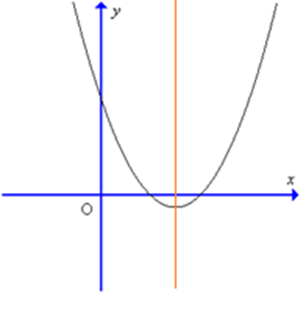
Kết luận nào sau đây đúng về hệ số a, b:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
Kết luận nào sau đây đúng về hệ số a, b:
Câu 7:
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
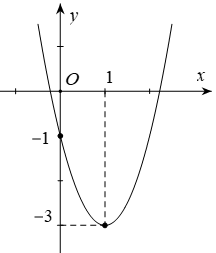
Cho parabol (P): y = ax2 + bx + c có đồ thị như hình bên. Phương trình của parabol này là :
Câu 8:
Số giá trị nguyên của x thỏa mãn điều kiện xác định của phương trình :\(\sqrt {2 - x} + \frac{4}{{\sqrt {x + 1} + 3}} = 1\) là:
Số giá trị nguyên của x thỏa mãn điều kiện xác định của phương trình :\(\sqrt {2 - x} + \frac{4}{{\sqrt {x + 1} + 3}} = 1\) là:
Câu 11:
Tổng các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
Tổng các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
Câu 12:
Cho hàm số y = f(x) có đồ thị như hình sau:
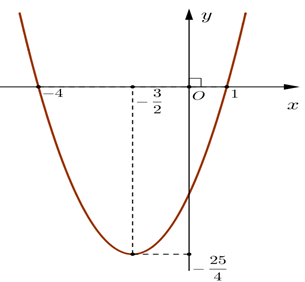
Hàm số đồng biến trên khoảng
Cho hàm số y = f(x) có đồ thị như hình sau:
Hàm số đồng biến trên khoảng
Câu 13:
Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
Câu 15:
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] là
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] là
