Câu hỏi:
08/11/2024 3,062
Cho tam giác ABC có b = 7; c = 5, . Đường cao của tam giác ABC là
A.
B. 8
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Lời giải:
Áp dụng định lí cosin trong tam giác ta có:
a2 = b2 + c2 = 2bc.cosA = 72 + 52 - 2.7.5.3/5 = 32
Nên
Mặt khác: sin2A + cos2A = 1 nên sin2A = 1 - cos2A =
Mà sinA > 0 nên sinA =
Mà:
*Phương pháp giải:
- Sử dụng định lí cosin trong tam giác khi biết được số đo hai cạnh và số đo của góc xen giữa hai cạnh đó.
- Sử dụng công thức lượng giác để tìm ra giá trị của góc cần tính.
- Áp dụng công thức tính diện tích tam giác.
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
* Lý thuyết nắm thêm và các công thức để tính diện tích tam giác"
Công thức tính diện tích tam giác
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
(Công thức Hê-rông)
Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
Định lí Côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
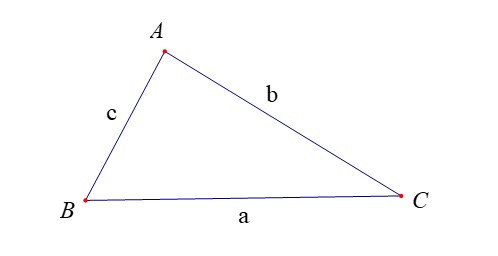
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
Định lí sin
Trong tam giác ABC: .
Giải tam giác và ứng dụng thực tế
- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.
Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:
+ Biết hai cạnh và góc xen giữa.
+ Biết ba cạnh.
+ Biết một cạnh và hai góc kề.
Xem thêm các bài viết liên quan hay, chi tiết:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho hình thang vuông ABCD có đáy lớn AB=4a, đáy nhỏ CD=2a, đường cao AD=3a. Tính
Câu 5:
Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc . Biết . Khoảng cách AB bằng bao nhiêu ?
Câu 6:
Cho , biết và . Để tính diện tích S của . Một học sinh làm như sau:
(I)Tính
(II)Tính
(III)
(IV)
Học sinh đó đã làm sai bắt đàu từ bước nào?
Cho , biết và . Để tính diện tích S của . Một học sinh làm như sau:
(I)Tính
(II)Tính
(III)
(IV)
Học sinh đó đã làm sai bắt đàu từ bước nào?


