Câu hỏi:
21/12/2024 2,681
Cho x,y là hai số thực bất kỳ thỏa và . Giá trị nhỏ nhất của .
A. 2.
B. 1.
C. 0.
D. 4.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là : D
Lời giải
Áp dụng bất đẳng thức Cô – si cho hai số không âm và .
Ta có:
Đẳng thức xảy ra
*Phương pháp giải
Áp dụng bất đẳng thức co si
*Lý thuyết:
- Khái quát: Bất đẳng thức Cosi, hay còn gọi là bất đẳng thức Cauchy, là một trong những bất đẳng thức cơ bản và phổ biến nhất trong toán học, đặc biệt là trong các bài toán liên quan đến bất đẳng thức và cực trị. Bất đẳng thức này được đặt theo tên của nhà toán học Augustin-Louis Cauchy, một trong những nhà toán học nổi tiếng của thế kỷ 19.
- Định lí: Trung bình nhân của hai số không âm nhỏ hơn hoặc bằng trung bình cộng của chúng.
Đẳng thức xảy ra khi và chỉ khi a = b.
Các hệ quả của BĐT Cô - si
+ Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.
,
+ Nếu x, y cùng dương và có tổng không đổi thì tích (xy) lớn nhất khi và chỉ khi x = y.
+ Trong tất cả các hình chữ nhật có cùng chu vi, hình vuông có diện tích lớn nhất.
+ Nếu x, y cùng dương và có tích không đổi thì tổng (x + y) nhỏ nhất khi và chỉ khi x = y.
+ Trong tất cả các hình chữ nhật có cùng diện tích, hình vuông có chu vi nhỏ nhất.
Các công thức
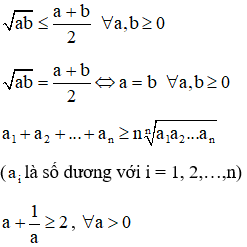
, nếu không đổi thì .
, nếu không đổi thì .
Xem thêm
Bất đẳng thức Cô-si (Cauchy) và hệ quả (2025) chi tiết nhấtCÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 6:
Cho và xét ba bất đẳng thức (I) ; (II) ; (III) . Bất đẳng thức nào là đúng?
Câu 14:
Cho . Xét các bất đẳng thức:
I)
II)
III) .
Bất đẳng thức nào đúng?


