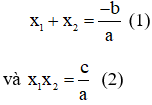Cho pt: x² - 2mx + m² - m + 1 = 0 (1)

Tìm m để pt (1) có nghiệm  x₁< x₂< 1

Đáp án đúng: D

*Lời giải

Đặt  t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:

t²+ 2(1-m) t+ m²- 3 m+2= 0  (2)

pt (1) có 2 nghiệm thỏa  x₁< x₂< 1 khi  và chỉ khi  pt (2) có 2 nghiệm:

(vô nghiệm)

Kết luận: không tồn tại m thỏa mãn bài toán.

*Phương pháp giải

- Ta có t1 < t2 < 0 nên cần các điều kiện để phương trình có hai nghiệm: 

+ Áp dụng định lý Vi - ét tìm:

 

 

 

Và cho > 0 

* Lý thuyết cần nắm và dạng toán về bất đẳng thức và bất phương trình:

a. Định nghĩa bất đẳng thức:

Các mệnh đề dạng “a > b” hoặc “a < b” được gọi là bất đẳng thức.

Nếu mệnh đề “a < b$\Rightarrow$ c < d” đúng thì ta nói bất đẳng thức c < d là bất đẳng thức hệ quả của bất đẳng thức a < b và cũng viết là a < b$\Rightarrow$ c < d.

Nếu bất đẳng thức a < b là hệ quả của bất đẳng thức c < d và ngược lại thì ta nói hai bất đẳng thức tương đương với nhau và viết là a < b $\iff$c < d.

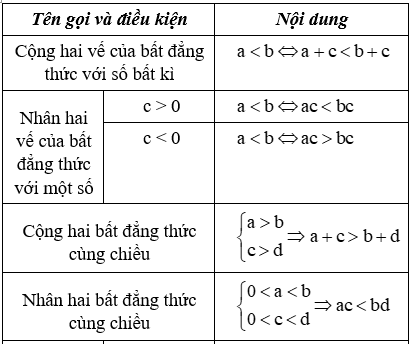
b. Tính chất của bất đẳng thức:

Chú ý

Ta còn gặp các mệnh đề dạng a ≤ b hoặc a ≥ b. Các mệnh đề dạng này cũng được gọi là bất đẳng thức. Để phân biệt, ta gọi chúng là các bất đẳng thức không ngặt và gọi các bất đẳng thức dạng a < b hoặc a > b là các bất đẳng thức ngặt. Các tính chất nêu trong bảng trên cũng đúng cho bất đẳng thức không ngặt.

c. Bất đẳng thức Cô-si:

$\forall a\ge 0;b\ge 0$ thì ta có: $\frac{a+b}{2}\ge \sqrt{ab}.$ Dấu “=” xảy ra khi và chỉ khi a=2

Hệ quả 1: Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.

$a+\frac{1}{a}\ge 2,\forall a>0.$

Hệ quả 2: Nếu hai số dương có tổng không đổi thì tích của chúng lớn nhất khi hai số bằng nhau.

Hệ quả 3: Nếu hai số dương có tích không đổi thì tổng của chúng nhỏ nhất khi hai số bằng nhau.

d. Bất đẳng thức chứa dấu giá trị tuyệt đối:

Ta có các tính chất cho trong bảng sau:

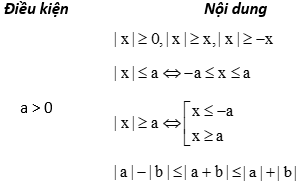
2. Các dạng toán

Dạng 1.1: Chứng minh bất đẳng thức nhờ định nghĩa

Để chứng minh $A\ge B$ (hoặc A > B), ta làm các bước sau:

Bước 1: xét hiệu A – B.

Bước 2: chứng minh $A-B\ge 0$ ( hoặc A – B > 0).

Sử dụng linh hoạt kiến thức ở phần lý thuyết để chứng minh ở bước 2.

Bước 3: kết luận.

Bước 4: xét A = B khi nào?

Dạng 1.2: Sử dụng bất đẳng thức Cô-si

Một số chú ý khi sử dụng bất đẳng thức Cô-si:

- Khi áp dụng bất đẳng thức Cô-si thì các số phải là những số không âm

- Bất đẳng thức Cô-si thường được áp dụng khi trong bất đẳng thức cần chứng minh có tổng và tích

- Điều kiện xảy ra dấu “=” là các số bằng nhau

- Bất đẳng thức Cô-si còn có hình thức khác thường hay sử dụng:

Đối với hai số: $x^2+y^2\ge 2xy;x+y\ge 2\sqrt{xy}$ với mọi $x;y\ge 0$

Đối với ba số:$abc\le \frac{a^3+b^3+c^3}{3}$ ; $a+b+c\ge 3\sqrt[3]{3abc}$ với mọi $a;b;c\ge 0$

Dạng 1.3: Tìm giá trị lớn nhất, giá trị nhỏ nhất của một đại lượng nhờ bất đẳng thức

Vận dụng các tính chất của bất đẳng thức, bất đẳng thức Cô-si, bất đẳng thức chứa dấu giá trị tuyệt đối,… để tìm giá trị lớn nhất, giá trị nhỏ nhất.

Xem thêm các bài viết liên quan hay, chi tiết

Các tính chất của bất đẳng thức lớp 10 (2024) đầy đủ, chi tiết 

Bất phương trình bậc nhất và cách giải bài tập (2024) chi tiết nhất