Câu hỏi:
09/11/2024 872
Cho hình vuông ABCD tâm O cạnh a. Tính tích vô hướng →AC.→BD.
Cho hình vuông ABCD tâm O cạnh a. Tính tích vô hướng →AC.→BD.
A. a;
B. 0;
C. a2;
D. 2a2.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B.
Lời giải

Do ABCD là hình vuông nên BD vuông góc với AC ⇒→AC.→BD=0.
*Phương pháp giải:
Dựa vào công thức tính tích vô hướng
*Lý thuyết:
Trong không gian có hai vecto →u ; →v đều khác vecto- không . Tích vô hướng của hai vecto là một số, kí hiệu là →u ; →v, được xác định bởi công thức: →u . →v = |→u|. |→v|.cos (→u; →v)
Trường hợp →u= →0 hoặc →v= →0 ta quy ước: →u . →v = 0.
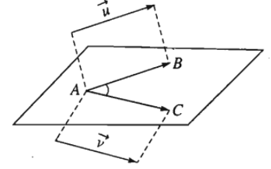
Trong không gian, cho →u ; →v là hai vecto khác vecto- không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho →AB = →u ; →AC = →v. Khi đó, ta gọi góc ^BAC (00 ≤^BAC ≤1800) là góc giữa hai vecto →u ; →v trong không gian.
Kí hiệu là (→u ; →v).
Xem thêm
Lý thuyết Hai đường thẳng vuông góc (mới + Bài Tập) - Toán 11
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →AB.→DC.
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →AB.→DC.
Câu 4:
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →BD.→BC.
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →BD.→BC.
Câu 6:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính tích vô hướng →AH.→AC.
Cho tam giác ABC đều cạnh a, đường cao AH. Tính tích vô hướng →AH.→AC.
Câu 7:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính vô hướng giữa hai vectơ →BA và →HC bằng
Cho tam giác ABC đều cạnh a, đường cao AH. Tính vô hướng giữa hai vectơ →BA và →HC bằng


