Câu hỏi:
18/07/2024 198
Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính →AB.→AO=?
Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính →AB.→AO=?
A. a;
B. 0;
C. a2;
D. 2a2.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D.
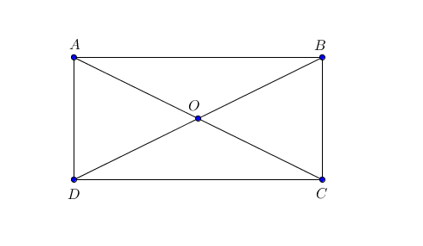
Do ABCD là hình chữ nhật nên ta có: BC = AD = a, AB = CD = 2a
Xét tam giác ABC vuông tại B
Áp dụng định lí Pythagore ta có:
AC2 = AB2 + BC2 = (2a)2 + a2 = 5a2
⇔ AC = a√5
⇒AO=12AC=12.a√5=a√52
Ta có:
(→AB, →AO)=^BAO=^BAC
Suy ra cos^BAO=cos^BAC=ABAC=2aa√5=2√5
|→AB|=AB=2a
|→AO|=AO=a√52
Ta có: →AB.→AO=|→AB|.|→AO|cos^BAO=2a.a√52.2√5=2a2.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →AB.→DC.
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →AB.→DC.
Câu 4:
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →BD.→BC.
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính →BD.→BC.
Câu 6:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính tích vô hướng →AH.→AC.
Cho tam giác ABC đều cạnh a, đường cao AH. Tính tích vô hướng →AH.→AC.
Câu 8:
Cho tam giác ABC đều cạnh a, đường cao AH. Tính vô hướng giữa hai vectơ →BA và →HC bằng
Cho tam giác ABC đều cạnh a, đường cao AH. Tính vô hướng giữa hai vectơ →BA và →HC bằng


