Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính $\overrightarrow{AB}.\overrightarrow{DC}$.

Đáp án đúng là: B.

* Phương pháp giải:

- Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức.

* Lời giải:

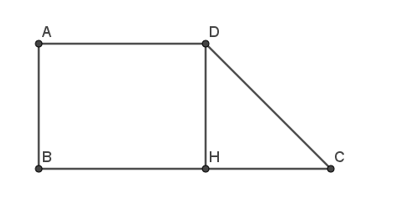
Kẻ DH vuông góc với BC tại H.

Do ABCD là hình thang vuông có đường cao AB nên AB = DH = 2a và AB // DH.

$\Rightarrow \overrightarrow{AB}=\overrightarrow{DH}\Rightarrow \left(\overrightarrow{AB},\overrightarrow{DC}\right)=\left(\overrightarrow{DH},\overrightarrow{DC}\right)=\widehat{CDH}$.

Xét hình thang vuông ABCD có:

BH = AD ⇔ HC = BC – BH = BC – AD = 3a – 2a = a

Xét tam giác DHC vuông tại H

Áp dụng định lí Pythagore ta có:

DC² = DH² + HC² = (2a)² + a² = 5a²

$\Rightarrow DC=a\sqrt{5}$

Do đó, $\cos \widehat{HDC}=\frac{DH}{DC}=\frac{2a}{a\sqrt{5}}=\frac{2}{\sqrt{5}}$

$\left|\overrightarrow{AB}\right|=AB=2a;\left|\overrightarrow{DC}\right|=DC=a\sqrt{5}$

Ta có: $\overrightarrow{AB}.\overrightarrow{DC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{DC}\right|.\cos \widehat{HDC}=2a.a\sqrt{5}.\frac{2}{\sqrt{5}}=4a^2$.

* Một số dạng bài tập về tích vô hướng của hai vectơ:

Dạng 1: Tính tích vô hướng của hai vectơ, góc giữa hai vectơ.

Phương pháp giải:

- Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức $\overrightarrow{a}.\overrightarrow{b}=a_1{b}_1+a_2{b}_2$

- Tính góc giữa hai vectơ: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc dùng công thức: $\cos \left(\overrightarrow{a};\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{a_1{b}_1+a_2{b}_2}{\sqrt{a_1^2+a_2^2}.\sqrt{b_1^2+b_2^2}}$

Dạng 2: Tính độ dài đoạn thẳng, độ dài vectơ.

Phương pháp giải:

Phân tích vectơ để biến phép tính độ dài đoạn thẳng thành phép tính tích vô hướng, áp dụng công thức $A{B}^2={\left|\overrightarrow{AB}\right|}^2={\overrightarrow{AB}}^2$. Nếu đề bài có liên quan đến tọa độ thì áp dụng công thức: $\left|\overrightarrow{AB}\right|=AB=\sqrt{{\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2}$.

Dạng 3: Chứng minh vuông góc.

Phương pháp giải:

Dùng tích chất của tích vô hướng để chứng minh vuông góc:

$$\begin{gathered} \overrightarrow{a}\perp \overrightarrow{b}\iff \overrightarrow{a}.\overrightarrow{b}=0 \\ \iff \left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|.\cos \left(\overrightarrow{a},\overrightarrow{b}\right)=0 \\ \iff \left[\begin{array}{l}\overrightarrow{a}=\overrightarrow{0}\\ \overrightarrow{b}=\overrightarrow{0}\\ \cos \left(\overrightarrow{a},\overrightarrow{b}\right)=0\end{array}\right. \end{gathered}$$

Hoặc dùng công thức về tọa độ: $\overrightarrow{a}\perp \overrightarrow{b}\iff a_1{b}_1+a_2{b}_2=0$

Dạng 4: Chứng minh các đẳng thức về tích vô hướng hay độ dài.

Phương pháp giải:

Áp dụng định nghĩa và tính chất của tích vô hướng, các quy tắc phân tích, biến đổi vectơ, các công thức về độ dài vectơ để biến đổi sao cho hai vế bằng nhau hoặc từ giả thiết suy ra một biểu thức luôn đúng đã được công nhận. Để chứng minh $\overrightarrow{v}=\overrightarrow{0}$ ta có thể chứng minh tích vô hướng của $\overrightarrow{v}$ với hai vectơ khác không cùng phương bằng 0.

Xem thêm các bài viết liên quan hay, chi tiết

Tích vô hướng của hai vectơ và cách giải bài tập (2024) chi tiết nhất

Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án

80 câu trắc nghiệm Vectơ cơ bản

•