10 câu hỏi trắc nghiệm thuộc Dạng 2: Cách tính tích vô hướng của hai vectơ có đáp án

Câu 1:

18/07/2024

Cho hình vuông ABCD tâm O cạnh a. Tính tích vô hướng $\vec{O A} . \vec{O D}$ .

A. 0;

B. 2a;

C. a²;

D. 2a².

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Cho hình vuông ABCD tâm O cạnh a. Tính tích vô hướng vecto OA, vecto OD (ảnh 1)

Do ABCD là hình vuông nên BD vuông góc với AC tại O.

Suy ra $O A ⊥ O D \Leftrightarrow \vec{O A} ⊥ \vec{O D} \Leftrightarrow \vec{O A} . \vec{O D} = 0$ .

Câu 2:

09/11/2024

Cho hình vuông ABCD tâm O cạnh a. Tính tích vô hướng $\vec{A C} . \vec{B D}$ .

A. a;

B. 0;

C. a²;

D. 2a².

Xem đáp án

Đáp án đúng là: B.

Lời giải

Cho hình vuông ABCD tâm O cạnh a. Tính tích vô hướng vecto AC.BD (ảnh 1)

Do ABCD là hình vuông nên BD vuông góc với AC $\Rightarrow \vec{A C} . \vec{B D} = 0$ .

*Phương pháp giải:

Dựa vào công thức tính tích vô hướng

*Lý thuyết:

Trong không gian có hai vecto $\vec{u}; \vec{v}$ đều khác vecto- không . Tích vô hướng của hai vecto là một số, kí hiệu là $\vec{u}; \vec{v}$ , được xác định bởi công thức: $\vec{u} . \vec{v} = |\vec{u}| . |\vec{v}| . c os (\vec{u}; \vec{v})$

Trường hợp $\vec{u} = \vec{0}$ hoặc $\vec{v} = \vec{0}$ ta quy ước: $\vec{u} . \vec{v}$ = 0.

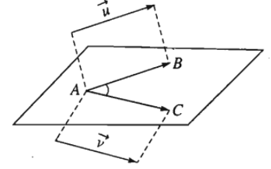
Trong không gian, cho $\vec{u}; \vec{v}$ là hai vecto khác vecto- không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho $\vec{A B} = \vec{u}; \vec{A C} = \vec{v}$ . Khi đó, ta gọi góc $\hat{B A C} (0^{0} \leq \hat{B A C} \leq 180^{0})$ là góc giữa hai vecto $\vec{u}; \vec{v}$ trong không gian.

Kí hiệu là ( $\vec{u}; \vec{v}$ ).

Xem thêm

Lý thuyết Hai đường thẳng vuông góc (mới + Bài Tập) - Toán 11

TOP 40 câu Trắc nghiệm Hai đường thẳng vuông góc (có đáp án ) – Toán 11

Câu 3:

18/07/2024

Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính $\vec{A B} . \vec{A O} = ?$

A. a;

B. 0;

C. a²;

D. 2a².

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

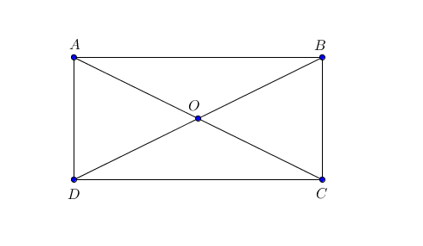
Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính vecto AB. AO (ảnh 1)

Do ABCD là hình chữ nhật nên ta có: BC = AD = a, AB = CD = 2a

Xét tam giác ABC vuông tại B

Áp dụng định lí Pythagore ta có:

AC² = AB² + BC² = (2a)² + a² = 5a²

⇔ AC = a $\sqrt{5}$

$\Rightarrow A O = \frac{1}{2} A C = \frac{1}{2} . a \sqrt{5} = \frac{a \sqrt{5}}{2}$

Ta có:

$(\vec{A B}, \vec{A O}) = \hat{B A O} = \hat{B A C}$

Suy ra $\cos \hat{B A O} = \cos \hat{B A C} = \frac{A B}{A C} = \frac{2 a}{a \sqrt{5}} = \frac{2}{\sqrt{5}}$

$|\vec{A B}| = A B = 2 a$

$|\vec{A O}| = A O = \frac{a \sqrt{5}}{2}$

Ta có: $\vec{A B} . \vec{A O} = |\vec{A B}| . |\vec{A O}| \cos \hat{B A O} = 2 a . \frac{a \sqrt{5}}{2} . \frac{2}{\sqrt{5}} = 2 a^{2}$ .

Câu 4:

20/07/2024

Cho tam giác ABC đều cạnh a. Tính $\vec{A B} . \vec{A C}$ .

A. a;

B. 0;

C. a²;

D.

\frac{1}{2} a^{2}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Do tam giác ABC đều nên:

AB = AC = a $\Rightarrow |\vec{A B}| = |\vec{A C}| = a$

$(\vec{A B}, \vec{A C}) =$ $\hat{B A C} = 60 ° \Rightarrow \cos \hat{B A C} = \frac{1}{2}$

Ta có:

$\vec{A B} . \vec{A C} = |\vec{A B}| . |\vec{A C}| . \cos \hat{B A C} = a . a . \frac{1}{2} = \frac{1}{2} a^{2}$ .

Câu 5:

18/07/2024

Cho tam giác ABC đều cạnh a, đường cao AH. Tính tích vô hướng $\vec{A H} . \vec{A C} .$

A.

\frac{3}{2} a^{2}

;

B. 3a²;

C.

\frac{3}{4} a^{2}

;

D. a².

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

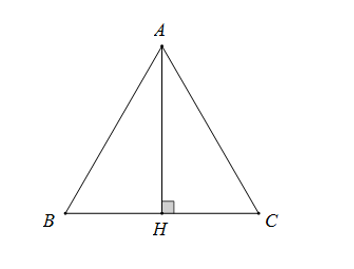
Cho tam giác ABC đều cạnh a, đường cao AH. Tính tích vô hướng vecto AH.vecto AC (ảnh 1)

Do tam giác ABC đều nên:

AH vừa là đường cao vừa là trung tuyến

$\Rightarrow B H = C H = \frac{B C}{2} = \frac{a}{2}$

Xét tam giác AHC vuông tại H

Áp dụng định lí Pythagore có:

AH² + CH² = AC² ⇔ AH² = AC² – CH² = $a^{2} - {(\frac{a}{2})}^{2} = \frac{3 a^{2}}{4} \Leftrightarrow A H = \frac{a \sqrt{3}}{2}$

$(\vec{A H}, \vec{A C}) = \hat{H A C}$ ; $\cos \hat{H A C} = \frac{A H}{A C} = \frac{\frac{a \sqrt{3}}{2}}{a} = \frac{\sqrt{3}}{2}$

Ta có: $\vec{A H} . \vec{A C} = |\vec{A H}| . |\vec{A C}| . \cos H A C = \frac{a \sqrt{3}}{2} . a . \frac{\sqrt{3}}{2} = \frac{3}{4} a^{2}$ .

Câu 6:

21/07/2024

Cho tam giác ABC đều cạnh a, đường cao AH. Tính vô hướng giữa hai vectơ $\vec{B A}$ và $\vec{H C}$ bằng

A. $\frac{a^{2}}{2}$

B. a²;

C. $\frac{a^{2}}{4}$

D. 2a².

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

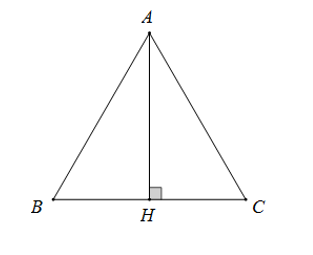
Cho tam giác ABC đều cạnh a, đường cao AH. Tính vô hướng giữa hai vectơ (ảnh 1)

Do tam giác ABC đều nên:

AH vừa là đường cao vừa là trung tuyến

$\Rightarrow B H = C H = \frac{B C}{2} = \frac{a}{2}$

Ta có:

$\vec{B H} = \vec{H C} \Rightarrow (\vec{B A}, \vec{H C}) = (\vec{B A}, \vec{B H}) = \hat{A B H} = 60 ° \Rightarrow c o s \hat{A B H} = \frac{1}{2}$

$|\vec{B A}| = A B = a; |\vec{H C}| = H C = \frac{a}{2}$

Vậy $\vec{B A} . \vec{H C} = |\vec{B A}| . |\vec{H C}| . \cos \hat{A B H} = a . \frac{a}{2} . \frac{1}{2} = \frac{a^{2}}{4}$ .

Câu 7:

11/10/2024

Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính $\vec{A B} . \vec{D C}$ .

A. a²;

B. 4a²;

C. 3a²;

D. 2a².

Xem đáp án

Đáp án đúng là: B.

* Phương pháp giải:

- Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức.

* Lời giải:

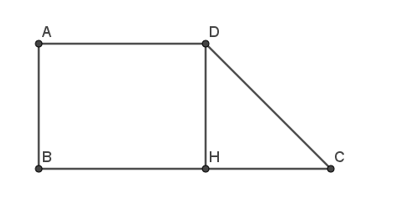
Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. (ảnh 1)

Kẻ DH vuông góc với BC tại H.

Do ABCD là hình thang vuông có đường cao AB nên AB = DH = 2a và AB // DH.

$\Rightarrow \vec{A B} = \vec{D H} \Rightarrow (\vec{A B}, \vec{D C}) = (\vec{D H}, \vec{D C}) = \hat{C D H}$ .

Xét hình thang vuông ABCD có:

BH = AD ⇔ HC = BC – BH = BC – AD = 3a – 2a = a

Xét tam giác DHC vuông tại H

Áp dụng định lí Pythagore ta có:

DC² = DH² + HC² = (2a)² + a² = 5a²

$\Rightarrow D C = a \sqrt{5}$

Do đó, $\cos \hat{H D C} = \frac{D H}{D C} = \frac{2 a}{a \sqrt{5}} = \frac{2}{\sqrt{5}}$

$|\vec{A B}| = A B = 2 a; |\vec{D C}| = D C = a \sqrt{5}$

Ta có: $\vec{A B} . \vec{D C} = |\vec{A B}| . |\vec{D C}| . \cos \hat{H D C} = 2 a . a \sqrt{5} . \frac{2}{\sqrt{5}} = 4 a^{2}$ .

* Một số dạng bài tập về tích vô hướng của hai vectơ:

Dạng 1: Tính tích vô hướng của hai vectơ, góc giữa hai vectơ.

Phương pháp giải:

- Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức $\vec{a} . \vec{b} = a_{1} b_{1} + a_{2} b_{2}$

- Tính góc giữa hai vectơ: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc dùng công thức: $\cos (\vec{a}; \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{a_{1} b_{1} + a_{2} b_{2}}{\sqrt{a_{1}^{2} + a_{2}^{2}} . \sqrt{b_{1}^{2} + b_{2}^{2}}}$

Dạng 2: Tính độ dài đoạn thẳng, độ dài vectơ.

Phương pháp giải:

Phân tích vectơ để biến phép tính độ dài đoạn thẳng thành phép tính tích vô hướng, áp dụng công thức $A B^{2} = {|\vec{A B}|}^{2} = {\vec{A B}}^{2}$ . Nếu đề bài có liên quan đến tọa độ thì áp dụng công thức: $|\vec{A B}| = A B = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}}$ .

Dạng 3: Chứng minh vuông góc.

Phương pháp giải:

Dùng tích chất của tích vô hướng để chứng minh vuông góc:

$\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = 0 \Leftrightarrow |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b}) = 0 \Leftrightarrow [\begin{array}{l} \vec{a} = \vec{0} \\ \vec{b} = \vec{0} \\ \cos (\vec{a}, \vec{b}) = 0 \end{array}$

Hoặc dùng công thức về tọa độ: $\vec{a} ⊥ \vec{b} \Leftrightarrow a_{1} b_{1} + a_{2} b_{2} = 0$

Dạng 4: Chứng minh các đẳng thức về tích vô hướng hay độ dài.

Phương pháp giải:

Áp dụng định nghĩa và tính chất của tích vô hướng, các quy tắc phân tích, biến đổi vectơ, các công thức về độ dài vectơ để biến đổi sao cho hai vế bằng nhau hoặc từ giả thiết suy ra một biểu thức luôn đúng đã được công nhận. Để chứng minh $\vec{v} = \vec{0}$ ta có thể chứng minh tích vô hướng của $\vec{v}$ với hai vectơ khác không cùng phương bằng 0.

Xem thêm các bài viết liên quan hay, chi tiết

Tích vô hướng của hai vectơ và cách giải bài tập (2024) chi tiết nhất

Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án

80 câu trắc nghiệm Vectơ cơ bản

Câu 8:

20/07/2024

Cho hình thang vuông ABCD, đường cao AB = 2a, đáy lớn BC = 3a, đáy nhỏ AD = 2a. Tính $\vec{B D} . \vec{B C}$ .

A. a²;

B. 4a²;

C. 6a²;

D. 2a².

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

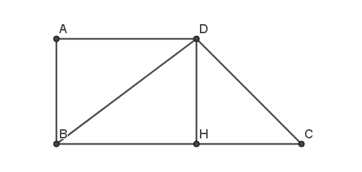
Kẻ DH vuông góc với BC, nối B với D.

Do ABCD là hình thang vuông có đường cao AB nên AB = DH = 2a và AB // DH

Xét tam giác BAD vuông tại A

Áp dụng định lí Pythagore ta có:

BD² = AB² + AD² = (2a)² + (2a)² = 8a²

$\Rightarrow B D = 2 \sqrt{2} a$

$(\vec{B D}, \vec{B C}) = \hat{D B C} = \hat{D B H}$

$\Rightarrow \cos (\vec{B D}, \vec{B C}) = \cos \hat{D B H} = \frac{B H}{B D} = \frac{2 a}{2 \sqrt{2} a} = \frac{1}{\sqrt{2}}$ .

Ta có:

$\vec{B D} . \vec{B C} = |\vec{B D}| . |\vec{B C}| . \cos \hat{D B H} = 2 \sqrt{2} a .3 a . \frac{1}{\sqrt{2}} = 6 a^{2}$ .

Câu 9:

18/07/2024

Cho tam giác ABC có: AB = 3, BC = 4, AC = 5. Tính $\vec{B A} . \vec{B C}$ .

A. 1

B. 0

B. 12

D. 20

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Xét tam giác ABC có:

AB² + BC² = 3² + 4² = 25

AC² = 5² = 25

⇔ AC² = AB² + BC²

Vậy tam giác ABC vuông tại B (theo định lí Pythagore đảo)

⇒ BA ⊥ BC

$\Rightarrow \vec{B A} . \vec{B C} = 0$ .

Câu 10:

18/07/2024

Cho tam giác ABC vuông tại A. Biết BC = a, $\hat{B C A} = 60 °$ . Tính $\vec{B C} . \vec{B A}$ .

A. a²;

B.

\frac{3}{4}

a²;

C.

\frac{1}{4}

a²;

D. 2a².

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

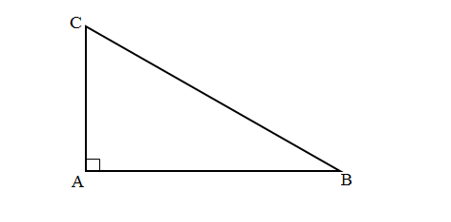
Cho tam giác ABC vuông tại A. Biết BC = a, góc BCA=60 độ. Tính vecto BC.BA (ảnh 1)

Xét tam giác ABC vuông tại A

Ta có:

$(\vec{B C}, \vec{B A}) = \hat{C B A} = 90 ° - \hat{B C A} = 90 ° - 60 ° = 30 °$

$\Rightarrow \cos (\vec{B C}, \vec{B A}) = \cos \hat{C B A} = \frac{\sqrt{3}}{2}$ .

Lại có: $B A = B C . \sin \hat{B C A} = B C . \sin 60 ° = \frac{\sqrt{3} a}{2}$ .

$|\vec{B C}| = B C = a, |\vec{B A}| = B A = \frac{a \sqrt{3}}{2}$ .

Vậy ta có:

$\vec{B C} . \vec{B A} = |\vec{B C}| . |\vec{B A}| . \cos \hat{C B A} = a . \frac{a \sqrt{3}}{2} . \frac{\sqrt{3}}{2} = \frac{3}{4} a^{2}$ .

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3