• Logo VietJack.me
×
Trang chủ Lớp 10 Toán Trắc nghiệm Toán 10 CTST Bài 4. Tích vô hướng của hai vectơ có đáp án

Trắc nghiệm Toán 10 CTST Bài 4. Tích vô hướng của hai vectơ có đáp án

Dạng 1: Xác định góc giữa hai vectơ có đáp án

  • 959 lượt thi

  • 10 câu hỏi

  • 30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

21/07/2024

Cho tam giác ABC vuông cân tại A. Tính góc giữa hai vectơ CA→ và BC→.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

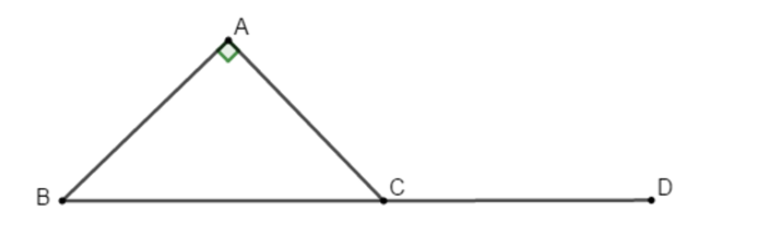
Cho tam giác ABC vuông cân tại A. Tính góc giữa hai vectơ CA và vecto BC. (ảnh 1)

Trên tia đối của CB lấy D sao cho CB = CD

Ta có: CD→=BC→

Khi đó: CA→,  BC→=CA→,  CD→=ACD^

Do tam giác ABC vuông cân tại A nên ACB^=45°.

Ta có: ACD^+ACB^=180° (hai góc kề bù)

⇒ACD^=180°−ACB^=180°−45°=135°

Vậy CA→,BC→=135°.

Câu 2:

22/07/2024

Cho tam giác ABC đều. Tính góc AB→,AC→.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Xét tam giác ABC đều có: BAC^=60°

⇒AB→,AC→=BAC^=60°.

Câu 3:

22/07/2024

Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính CB→,CA→.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

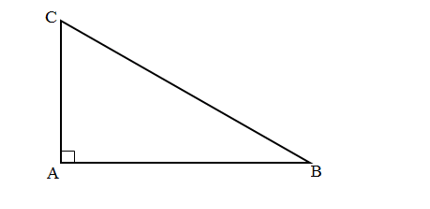
Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính ( vecto CB, vecto CA) (ảnh 1)

Xét tam giác ABC vuông tại A có:

sinACB^=ABBC=48=12⇒ACB^=30°

Vậy CB→,CA→=ACB^=30°.

Câu 4:

22/07/2024

Cho tam giác ABC vuông tại B. Có AB = 3, AC = 6. Tính AB→,AC→.
Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

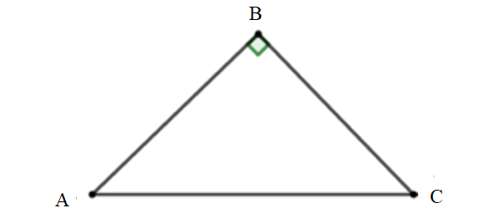
Cho tam giác ABC vuông tại B. Có AB = 3, AC = 6. Tính (vecto AB, vecto AC) (ảnh 1)

Xét tam giác ABC vuông tại A có:

cosBAC^=ABAC=36=12⇒CAB^=60°

Vậy AB→,AC→=CAB^=60°.

Câu 5:

22/07/2024

Cho tam giác ABC có AB = 5, AC = 6, BC = 4. Tính côsin của góc BA→,BC→.
Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Ta có: BA→,BC→=ABC^ 

Xét tam giác ABC

Áp dụng định lí côsin ta có:

cosABC^=BA2+BC2−AC22BA.BC=52+42−622.5.4=18

Vậy cosBA→,BC→=cosABC^=18.

Câu 6:

22/07/2024

Cho tam giác ABC có AB = 12, BC = 15, AC = 13. Tính cosAB→,AC→.
Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

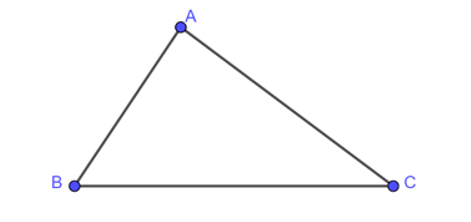
Cho tam giác ABC có AB = 12, BC = 15, AC = 13. Tính cos (vecto AB, vecto AC) (ảnh 1)

Ta có: AB→,AC→=BAC^

Xét tam giác ABC

Áp dụng định lí côsin ta có:

cosBAC^=AB2+AC2−BC22AB.AC=122+132−1522.12.13=1139

Vậy cosAB→,AC→=1139.

Câu 7:

22/07/2024

Cho hình vuông ABCD tâm O. Tính CA→,BA→.
Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

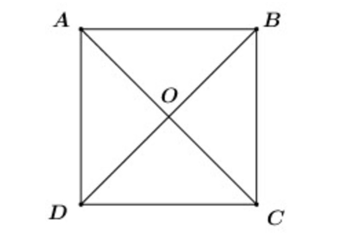
Cho hình vuông ABCD tâm O. Tính (vecto BA, vecto CA) (ảnh 1)

Xét hình vuông ABCD có: BA→=CD→

Do đó, CA→,BA→=CA→,CD→=ACD^

Xét tam giác ACD có:

DA = DC (do ABCD là hình vuông)

ADC^=90°

Do đó, tam giác ACD vuông cân tại D.

⇒ACD^=45°

Vậy CA→,BA→=45°.

Câu 8:

22/07/2024

Cho hình vuông ABCD tâm O. Tính OA→,OC→.
Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

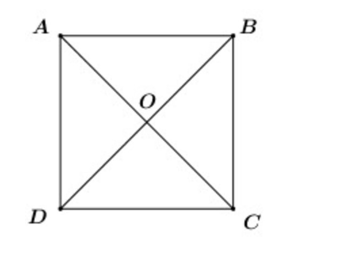
Cho hình vuông ABCD tâm O. Tính (vecto OA, vecto OC) (ảnh 1)

Ta có: OA→ và OC→ là hai vectơ cùng phương, ngược hướng.

Vậy OA→,OC→=180°.

Câu 9:

22/07/2024

Cho hình chữ nhật ABCD. Tính góc AB→,DC→.
Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Do ABCD là hình chữ nhật nên AB→,DC→ cùng hướng.

Vậy AB→,DC→=0°.

Câu 10:

22/07/2024

Cho hình thoi ABCD tâm O. Biết BD = 23, AC = 6. Tính BA→,BC→.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Hình thoi ABCD có tâm O nên O là trung điểm của hai đường chéo AC và BD, hơn nữa hai đường chéo này vuông góc với nhau tại O.

Do đó, ta có:

BD = 23⇒OB=3

AC = 6 ⇒ AO = 3.

Xét tam giác AOB vuông tại O có: tanABO^=AOOB=33⇒ABO^=60°.

Do ABCD là hình thoi nên BD là tia phân giác góc ABC^, do đó ta có:

ABC^=2ABO^=2.60°=120°.

Vậy BA→,BC→=ABC^=120°.

 

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương