Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số có đáp án
-
1203 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Cho tam giác đều ABC cạnh 4. Vectơ −12→BC có độ dài là.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Do tam giác ABC đều cạnh 4 nên: AB = AC = BC = 4
⇒ |→BC|=BC= 4
Ta có: |−12→BC|=|−12|.|→BC|=12.4=2.
Câu 2:
22/07/2024Cho hình vuông ABCD tâm O cạnh 3. Ta có |12→AC+12→DB| = ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Do O là tâm của hình vuông ABCD nên O là trung điểm của AC và BD nên ta có:
12→AC=→AO; 12→DB=→OB.
⇒12→AC+12→DB=→AO+→OB=→AB
⇒|12→AC+12→DB|=|→AB|=AB=3.
Câu 3:
22/07/2024Cho hình thoi ABCD cạnh 5 và ^ABC=60o. Tính: |2→AB+2→AD|.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
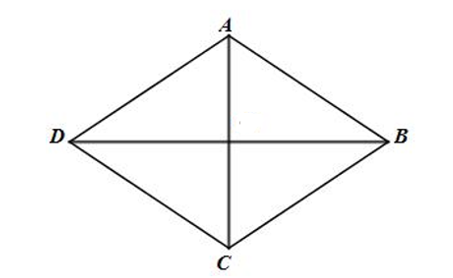
Ta có: 2→AB+2→AD=2(→AB+→AD)=2→AC (áp dụng quy tắc hình bình hành)
Xét tam giác ABC có:
^ABC=60o
AB = BC (do ABCD là hình thoi)
Do đó, tam giác ABC là tam giác đều
⇒ AC = AB = BC = 5
Vậy |2→AB+2→AD|=|2→AC|=|2||→AC|=2.AC=2.5=10.
Câu 4:
22/07/2024Cho hình thoi ABCD cạnh 5 và ^ABC=60o. Tính: |2→AB−2→AD|.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
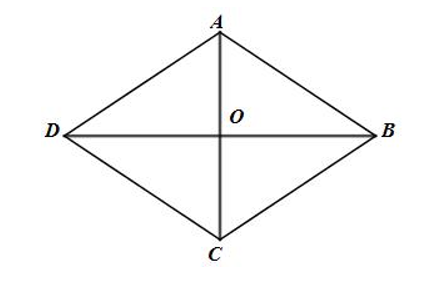
Ta có: 2→AB−2→AD=2(→AB−→AD)=2→DB (hiệu hai vectơ).
Gọi O là giao hai đường chéo của hình thoi, khi đó O là trung điểm của AC và BD. Hơn nữa hai đường chéo này vuông góc với nhau tại O.
Xét tam giác ABC có:
^ABC=60o
AB = BC (do ABCD là hình thoi)
Do đó, tam giác ABC là tam giác đều
⇒ AC = AB = BC = 5
⇒AO=12AC=12.5=2,5
Xét tam giác AOB vuông tại O, theo định lí Pytahgore ta có:
AB2=AO2+BO2⇒BO2=AB2−AO2=52−2,52=18,75
⇒BO=5√32
⇒BD=2BO=2.5√32=5√3
Vậy |2→AB−2→AD|=|2→DB|=|2||→DB|=2DB=2.5√3=10√3.
Câu 5:
22/07/2024Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ 12→DB.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
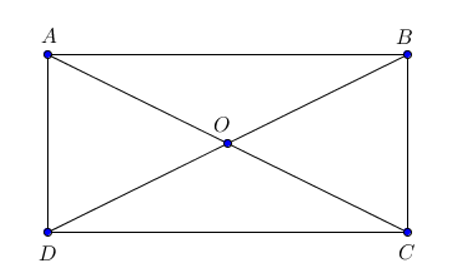
Xét tam giác ABD vuông tại A (do ABCD là hình chữ nhật)
Áp dụng định lí Pythagore ta có:
BD2 = AB2 + AD2 = 42 + 32 = 25 ⇔ BD = 5
Có: |12→DB|=|12||→DB|=12DB=12.5=2,5.
Câu 6:
22/07/2024Cho tam giác đều ABC cạnh a. Điểm M là trung điểm BC. Tính: |12→CB+→MA|.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
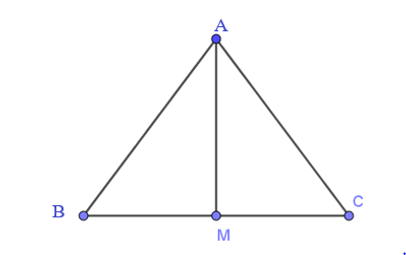
Do M là trung điểm của BC nên ta có: 12→CB=→CM
Do đó, ta có: 12→CB+→MA=→CM+→MA=→CA
Vậy |12→CB+→MA|=|→CA|=CA=a.
Câu 7:
22/07/2024Cho tam giác đều ABC cạnh a. Tính:|→BA−12→BC|.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
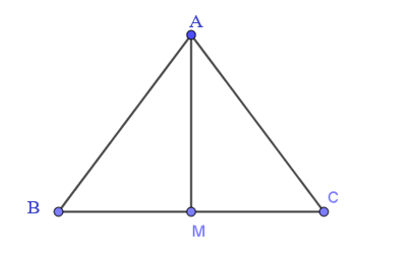
Gọi M là trung điểm của BC.
Do đó ta có: 12→BC=→BM
Khi đó: →BA−12→BC=→BA−→BM=→MA (hiệu hai vectơ)
⇔|→BA−12→BC|=|→MA|=MA.
Do tam giác ABC đều nên AM vừa là trung tuyến vừa là đường cao nên tam giác AMB vuông tại M.
Ta có: BM = 12BC=a2.
Áp dụng định lí Pythagore ta có:
AB2 = AM2 + BM2 ⇔ AM2 = AB2 – BM2 = a2 – (a2)2= 3a24 ⇔MA=a√32
Vậy |→BA−12→BC|=MA=a√32.
Câu 8:
22/07/2024Cho hình thoi ABCD tâm O cạnh a. Ta có |2→DO+→BC+2→CO| = ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
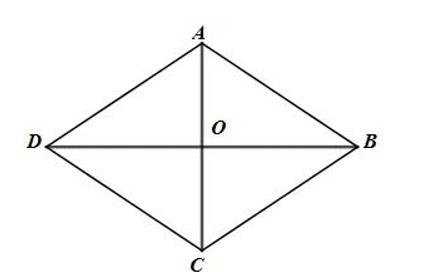
Vì O là tâm hình thoi ABCD nên O là trung điểm của AC và BD.
Do đó ta có:
2→DO=→DB;
2→CO=→CA.
Khi đó:
2→DO+→BC+2→CO=→DB+→BC+→CA=→DC+→CA=→DA (áp dụng quy tắc ba điểm)
Suy ra: |2→DO+→BC+2→CO|=|→DA| = DA = a.
Câu 9:
22/07/2024Cho hình vuông ABCD tâm O cạnh 2a. Vectơ tổng 2→AB+2→DC có độ dài là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
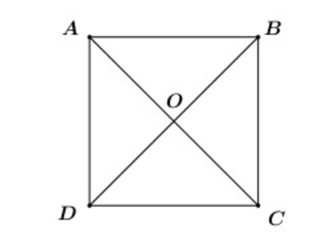
Xét hình vuông ABCD có: →AB=→DC
Ta có: |2→AB+2→DC|=|2→AB+2→AB|=|4→AB|=|4||→AB|=4.AB=4.2a=8a.
Câu 10:
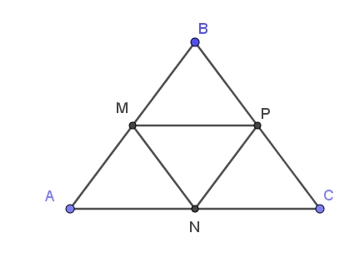
22/07/2024Cho tam giác ABC đều cạnh 4a. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Tính: |12→BA−12→BC|.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
12→BA=→BM (do M là trung điểm AB)
12→BC=→BP (do P là trung điểm BC)
|12→BA−12→BC|=|→BM−→BP|=|→PM|=PM (áp dụng quy tắc trừ hai vectơ)
Xét tam giác ABC đều
M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC
Do đó, PM là đường trung bình của tam giác ABC.
⇒PM=12AC=12.4a=2a
Vậy |12→BA−12→BC|=2a.