Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước có đáp án
-
1212 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
16/07/2024Điểm I thỏa mãn →IA+2→IB=→0 là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Theo quy tắc ba điểm, ta có: →IA+2→IB=→IA+2(→IA+→AB)=3→IA+2→AB.
Mà →IA+2→IB=→0
Do đó: 3→IA+2→AB=→0
⇔→IA=−23→AB⇔→IA=23→BA
Vậy I nằm trên nửa đường thẳng AB theo hướng từ B về A với IA=23AB.
Câu 2:
16/07/2024Điểm K thỏa mãn: →KA+2→KB=→CB là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
→KA+2→KB=→CB
⇔→KA+2→KB−→CB=→0
⇔→KA+→KB+(→KB+→BC)=→0
⇔→KA+→KB+→KC=→0
Vậy K là trọng tâm của tam giác ABC.
Câu 3:
23/07/2024Cho tam giác ABC. Điểm P thỏa mãn →CP=→KA+2→KB−3→KC với K tùy ý là điểm thỏa mãn:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
→CP=→KA+2→KB−3→KC
⇔→CP=(→KC+→CA)+2(→KC+→CB)−3→KC (quy tắc ba điểm)
⇔→CP=→CA+2→CB
Vậy tập hợp điểm P thỏa mãn →CP=→CA+2→CB.
Câu 4:
14/07/2024Cho tứ giác ABCD, I là trung điểm BD. Tìm điểm O thỏa mãn →OB+4→OC=2→OD
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
→OB+4→OC=2→OD
⇔→OB+4(→OB+→BC)=2(→OB+→BD) (quy tắc ba điểm)
⇔3→OB=2→BD−4→BC
⇔3→OB=2(→BD−→BC)−2→BC (quy tắc trừ hai vectơ)
⇔3→OB=2→BD−4→BC
⇔3→OB=2→BD+4→CB
⇔3→OB=2(→CB+→BD)+2→CB
⇔3→OB=2→CD+2→CB (quy tắc ba điểm)
⇔3→OB=4→CI (do I là trung điểm của BD nên →CD+→CB=2→CI)
⇔→OB=43→CI
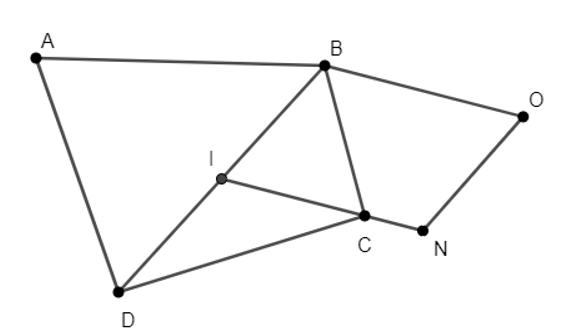
Vậy O là đỉnh của hình bình hành IBON với →IN=43→IC.
Câu 5:
20/07/2024Cho tứ giác ABCD và điểm O bất kì sao cho →OB+4→OC−2→OD=→0. Tìm điểm M thỏa mãn hệ thức |→MB+4→MC−2→MD|=|3→MA|.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
|→MB+4→MC−2→MD|=|3→MA|
⇔|(→MO+→OB)+4(→MO+→OC)−2(→MO+→OD)|=|3→MA| (quy tắc ba điểm)
⇔|3→MO+(→OB+4→OC−2→OD)|=|3→MA|
⇔|3→MO|=|3→MA| (do →OB+4→OC−2→OD=→0)
⇔|→MO|=|→MA|
⇔ MO = MA.
Vậy M thuộc đường trung trực của đoạn thẳng OA.
Câu 6:
14/07/2024Cho hai điểm A, B phân biệt. Xác định điểm M biết 2→MA−3→MB=→0.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có:
2→MA−3→MB=→0
⇔2→MA−3(→MA+→AB)=→0 (quy tắc ba điểm)
⇔−→MA−3→AB=→0
⇔→AM=3→AB
Vậy M nằm trên tia AB và AM = 3AB.
Câu 7:
14/07/2024Cho tứ giác ABCD. Gọi I là trung điểm của BC. Xác định điểm M sao cho: 2→MA+→MB+→MC=→0.
Xem đáp án
Đáp án đúng là: B.
Vì I là trung điểm của BC nên →MB+→MC=2→MI.
Ta có:
2→MA+→MB+→MC=→0
⇔2→MA+2→MI=→0
⇔→MA+→MI=→0.
Vậy M là trung điểm của AI.
Câu 8:
19/07/2024Cho tứ giác ABCD. Gọi G là trọng tâm của tam giác BCD. Xác định điểm P sao cho: →PB+→PC+→PD=3→AP.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Vì G là trọng tâm của tam giác BCD nên với điểm P thì →PB+→PC+→PD=3→PG.
Ta có:
→PB+→PC+→PD=3→AP
⇔→PB+→PC+→PD−3→AP=→0
⇔3→PA+(→PB+→PC+→PD)=→0
⇔3→PA+3→PG=→0
⇔→PA+→PG=→0.
Vậy P là trung điểm của AG.
Câu 9:
16/07/2024Cho tứ giác ABCD. Gọi K, H lần lượt là trung điểm của AB, CD. Xác định điểm N sao cho: →NA+→NB+→NC+→ND=→0.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Vì K, H lần lượt là trung điểm của AB, CD nên →NA+→NB=2→NK; →NC+→ND=2→NH.
Do đó ta có:
→NA+→NB+→NC+→ND=→0
⇔2→NK+2→NH=→0
⇔→NK+→NH=→0
Vậy N là trung điểm của KH.
Câu 10:
15/07/2024Cho tam giác ABC vuông tại A. Điểm M bất kì nằm trong tam giác có hình chiếu xuống BC, CA, AB theo thứ tự là D, E, F. Tìm tập hợp điểm M biết →MD+→ME+→MF cùng phương với →BC.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
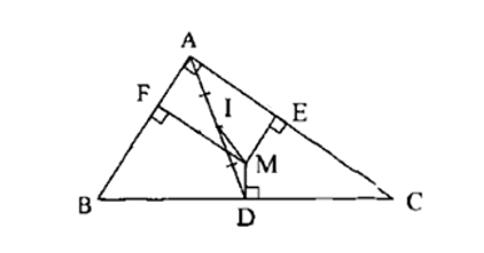
Xét tứ giác AEMF có: ^EAF=^AEM=^MFA=90°.
Do đó, AEMF là hình chữ nhật.
Áp dụng quy tắc hình bình hành ta có: .
Do đó ta có: .
Gọi I là trung điểm của AD.
Khi đó, .
Để cùng phương với thì cùng phương với
Do đó, cùng phương với (do PQ là đường trung bình của tam giác ABC song song với cạnh BC).
Vì M nằm trong tam giác ABC.
Do đó M thuộc đoạn PQ.