Câu hỏi:
19/07/2024 293
Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của DC, AB; P là giao điểm của AM, DB và Q là giao điểm của CN, DB. Khẳng định nào sau đây là đúng nhất.
A. .
B. .
C. Cả A, B đều đúng.
D. Cả A, B đều sai.
Trả lời:
Giải bởi Vietjack
Đáp án: C
Giải thích:
Lời giải
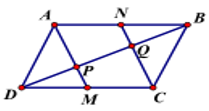
Ta có tứ giác DMBN là hình bình hành vì , . Suy ra .
Xét tam giác CDQ có M là trung điểm của DC và do đó P là trung điểm của DQ. Tương tự xét tam giác ABP suy ra được Q là trung điểm của PB
Vì vậy từ đó suy ra .
Đáp án: C
Giải thích:
Lời giải
Ta có tứ giác DMBN là hình bình hành vì , . Suy ra .
Xét tam giác CDQ có M là trung điểm của DC và do đó P là trung điểm của DQ. Tương tự xét tam giác ABP suy ra được Q là trung điểm của PB
Vì vậy từ đó suy ra .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho lục giác ABCDEF. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là đỉnh của lục giác.
Câu 6:
Cho hình bình hành ABCD tâm O. Gọi P, Q, R lần lượt là trung điểm AB, BC, AD. Lấy 8 điểm trên làm điểm gốc hoặc điểm ngọn các vectơ. Tìm mệnh đề sai:
Cho hình bình hành ABCD tâm O. Gọi P, Q, R lần lượt là trung điểm AB, BC, AD. Lấy 8 điểm trên làm điểm gốc hoặc điểm ngọn các vectơ. Tìm mệnh đề sai:
Câu 7:
Cho hình thang ABCD có hai đáy là AB và CD với . Từ C vẽ . Khẳng định nào sau đây là đúng nhất?
Câu 9:
Cho hai điểm phân biệt A, B. Số vectơ ( khác ) có điểm đầu và điểm cuối lấy từ các điểm A, B là:
Câu 10:
Cho khẳng định sau
(1). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì .
(2). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì .
(3). Nếu thì 4 điểm A, B, C, D là 4 đỉnh của hình bình hành.
(4). Nếu thì 4 điểm A, B, C, D theo thứ tự đó là 4 đỉnh của hình bình hành.
Hỏi có bao nhiêu khẳng định sai?
Cho khẳng định sau
(1). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì .
(2). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì .
(3). Nếu thì 4 điểm A, B, C, D là 4 đỉnh của hình bình hành.
(4). Nếu thì 4 điểm A, B, C, D theo thứ tự đó là 4 đỉnh của hình bình hành.
Hỏi có bao nhiêu khẳng định sai?
Câu 11:
Cho bốn điểm A, B, C, D phân biệt. Nếu thì có khẳng định nào sau đây đúng
Câu 14:
Cho hình bình hành ABCD. Trên các đoạn thẳng DC, AB theo thứ tự lấy các điểm M, N sao cho . Gọi P là giao điểm của AM, DB và Q là giao điểm của CN, DB. Khẳng định nào đúng?
Câu 15:
Cho lục giác đều ABCDEF tâm O. Số các vectơ bằng có điểm đầu và điểm cuối là đỉnh của lục giác là:
