Cho hàm số y = x² + 6x – 5. Khẳng định nào sau đây là đúng ?

Đáp án đúng là: B.

Lời giải

Xét hàm số y = x² + 6x – 5 có a = 1 > 0, b = 6, c = –5

Ta có: \(\frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.1}} = - 3\).

Do đó, hàm số nghịch biến trên khoảng (–∞; –3) và đồng biến trên khoảng (–3; +∞).

*Phương pháp giải:

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Tính denta tìm nghiệm 

Bước 3. Kết luận về các khoảng đồng biến và nghịch biến của hàm số.

*Lý thuyết:

- Định nghĩa:

Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:

Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x₁; x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x₁) nhỏ hơn f(x₂), tức là

x₁ < x₂ $\Rightarrow$ f(x₁) < f(x₂).

Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x₁; x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x₁) lớn hơn f(x₂), tức là

x₁ < x₂ $\Rightarrow$f(x₁) > f(x₂).

- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.

- Nhận xét: Từ định nghĩa trên ta thấy:

a) f(x) đồng biến trên K$\iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>\text{}0;$ $\hspace{0.17em}\forall x_1;x_2\in K;(x_1\ne x_2)$

f(x) nghịch biến trên K$\iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}<\text{\hspace{0.17em}}0;$$\hspace{0.17em}\forall x_1;x_2\in K;(x_1\ne x_2)$

b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.

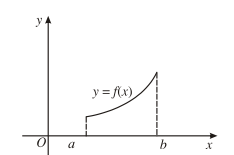
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.

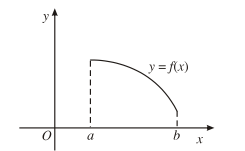
2. Tính đơn điệu và dấu của đạo hàm

- Định lí:

Cho hàm số y = f(x) có đạo hàm trên K.

a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

- Chú ý:

Nếu f’(x) = 0 với $\forall x\in \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}K$ thì f(x) không đổi trên K.

- Chú ý:

Ta có định lí mở rộng sau đây:

Giả sử hàm số y = f(x) có đạo hàm trên K. Nếu $f^{\text{'}}\left(x\right)\ge 0\left(f^{\text{'}}\left(x\right)\le 0\right);\forall x\in K$

Và f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.

Xem thêm

Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2 + Bài Tập) – Toán 12 

TOP 40 câu Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án 2) - Toán 12