Dạng 4: Xét sự biến thiên của hàm số bậc hai có đáp án
-
2599 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
21/07/2024
Xem đáp án
Hướng dẫn giải:
Xét hàm số y = –x2 + 4x + 5 có a = –1 < 0, b = 4, c = 5
Ta có: −b2a=−42.(−1)=2; −Δ4a=−b2−4ac4a=−(−4)2−4.(−1).54.(−1)=9.
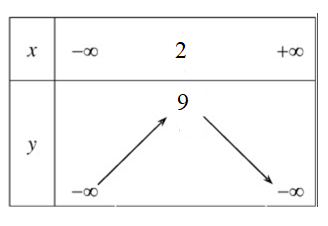
Do đó, hàm số đồng biến trên khoảng (–∞; 2), nghịch biến trên khoảng (2; +∞).
Bảng biến thiên:
Câu 2:
12/07/2024 Xem đáp án
Hướng dẫn giải:
Xét hàm số y = 2x2 + 2x + 1 có a = 2 > 0, b = 2, c = 1.
Ta có: −b2a=−22.2=−12; −Δ4a=−b2−4ac4a=−22−4.2.14.2=12.
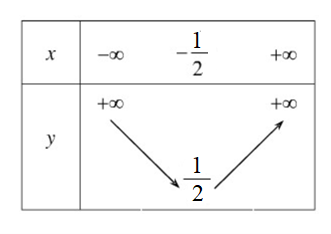
Do đó, hàm số nghịch biến trên khoảng (−∞;−12), đồng biến trên khoảng (−12;+∞).
Bảng biến thiên:
Câu 3:
19/07/2024Hàm số y = x2 – 4x + 5 đồng biến trên khoảng:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = x2 – 4x + 5 có a = 1 > 0, b = – 4, c = 5.
Ta có: −b2a=−(−4)2.1=2
Do đó, hàm số đồng biến trên khoảng (2; +∞)
Câu 4:
21/07/2024Hàm số y = –3x2 + 6x + 1 đồng biến trên khoảng:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số y = –3x2 + 6x + 1 có a = –3 < 0, b = 6, c = 1.
Ta có: −b2a=−62.(−3)=1.
Do đó, hàm số đồng biến trên khoảng (–∞; 1).
Câu 5:
18/07/2024Hàm số y = –x2 + 2x – 2 nghịch biến trên khoảng:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Xét hàm số y = –x2 + 2x – 2 có a = –1 < 0, b = 2, c = –2
Ta có: −b2a=−22.(−1)=1
Do đó, hàm số nghịch biến trên khoảng (1; +∞).
Câu 6:
12/07/2024Hàm số y = 4x2 – 24x – 6 nghịch biến trên khoảng:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = 4x2 – 24x – 6 có a = 4 > 0, b = –24, c = –6.
Ta có: −b2a=−(−24)2.4=3.
Do đó, hàm số nghịch biến trên khoảng (–∞; 3).
Câu 7:
18/07/2024Cho hàm số y = x2 – 4x – 6. Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số y = x2 – 4x – 6 có a = 1 > 0, b = –4, c = –6
Ta có: −b2a=−(−4)2.1=2.
Do đó, hàm số nghịch biến trên khoảng (–∞; 2) và đồng biến trên khoảng (2; + ∞).
Câu 8:
23/07/2024Cho hàm số y = –x2 + 8x – 3. Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Xét hàm số y = –x2 + 8x – 3 có a = –1 < 0, b = 8, c = –3
Ta có: −b2a=−82.(−1)=4
Do đó, hàm số đồng biến trên khoảng (–∞; 4) và nghịch biến trên (4; +∞).
Câu 9:
23/07/2024Cho hàm số y = –x2 + 4x – 3. Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = –x2 + 4x – 3 có a = –1 < 0, b = 4, c = –3
Ta có: −b2a=−42.(−1)=2
Do đó, hàm số đồng biến trên khoảng (–∞; 2) và nghịch biến trên khoảng (2; +∞).
Câu 10:
11/12/2024Cho hàm số y = x2 + 6x – 5. Khẳng định nào sau đây là đúng ?
Xem đáp án
Đáp án đúng là: B.
Lời giải
Xét hàm số y = x2 + 6x – 5 có a = 1 > 0, b = 6, c = –5
Ta có: −b2a=−62.1=−3.
Do đó, hàm số nghịch biến trên khoảng (–∞; –3) và đồng biến trên khoảng (–3; +∞).
*Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính denta tìm nghiệm
Bước 3. Kết luận về các khoảng đồng biến và nghịch biến của hàm số.
*Lý thuyết:
- Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:
Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) nhỏ hơn f(x2), tức là
x1 < x2 ⇒ f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) lớn hơn f(x2), tức là
x1 < x2 ⇒f(x1) > f(x2).
- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.
- Nhận xét: Từ định nghĩa trên ta thấy:
a) f(x) đồng biến trên K⇔f(x2)−f(x1)x2−x1 >0 ;
f(x) nghịch biến trên K
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.
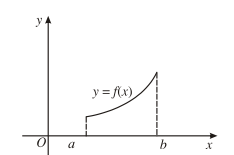
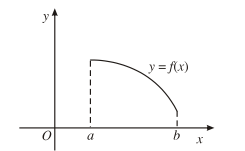
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.
2. Tính đơn điệu và dấu của đạo hàm
- Định lí:
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
- Chú ý:
Nếu f’(x) = 0 với thì f(x) không đổi trên K.
- Chú ý:
Ta có định lí mở rộng sau đây:
Giả sử hàm số y = f(x) có đạo hàm trên K. Nếu
Và f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.
Xem thêm
Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2 + Bài Tập) – Toán 12
Câu 11:
12/07/2024 Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Xét hàm số y = –x2 + 4x – 3 có a = –1 < 0, b = 4, c = –3
Ta có: \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.( - 1)}} = 2; \frac{{ - \Delta }}{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{4^2} - 4.( - 1).( - 3)}}{{4.( - 1)}} = 1.
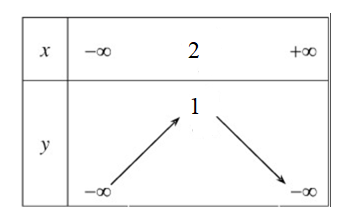
Do đó, hàm số đồng biến trên khoảng (–∞; 2), nghịch biến trên khoảng (2; +∞).
Bảng biến thiên:
Câu 12:
20/07/2024Đâu là bảng biến thiên của hàm số y = x2 + 6x – 5 ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số y = x2 + 6x – 5 có a = 1 > 0, b = 6, c = –5
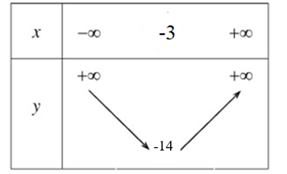
Ta có: \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.1}} = - 3; \frac{{ - \Delta }}{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{6^2} - 4.1.( - 5)}}{{4.1}} = - 14.
Do đó, hàm số nghịch biến trên khoảng (–∞; –3), đồng biến trên khoảng (–3; +∞)
Bảng biến thiên:
