Thi Online Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án
Dạng 1: Tìm tổng của hai hay nhiều vectơ có đáp án
-
1018 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
14/07/2024Cho O là trung điểm của AB. Ta có:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Áp dụng tính chất giao hoán và quy tắc ba điểm cho ba điểm A, O, B ta có:
.
Câu 2:
22/07/2024Cho 4 điểm A, B, C, D. Ta có:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Áp dụng quy tắc ba điểm cho ba điểm A, D, B ta có: .
Áp dụng quy tắc ba điểm cho ba điểm A, D, C ta có: .
Vậy .
Câu 3:
13/07/2024Cho các điểm A, B, C phân biệt. Đẳng thức nào sau đây đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Áp dụng tính chất giao hoán và quy tắc ba điểm cho ba điểm A, C, B ta có:
Vậy .
Câu 4:
15/07/2024Cho hình bình hành ABCD tâm O. Khi đó,
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
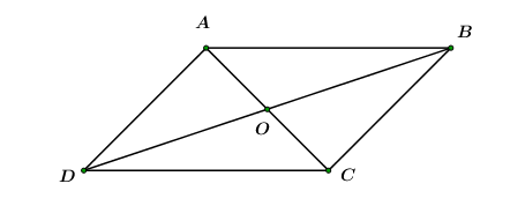
Áp dụng tính chất giao hoán và quy tắc ba điểm cho ba điểm A, O, B ta có: .
Xét hình bình hành ABCD có:
Vậy
Câu 5:
21/07/2024Cho hình vuông ABCD tâm O. Khi đó:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
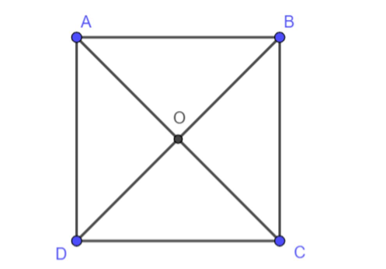
Áp dụng quy tắc hình bình hành cho hình vuông ABCD có: .
Câu 6:
12/07/2024Cho 6 điểm A, B, C, D, E, F. Đẳng thức nào sau đây đúng.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
Vậy .
Câu 7:
12/07/2024Cho các điểm M, N, P, Q, R. Tính = ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
Vậy .
Câu 8:
10/10/2024Cho hình bình hành ABCD tâm O. Khẳng định nào sau đây là đúng ?
Xem đáp án
Đáp án đúng là: D.
*Phương pháp giải:
Dùng định nghĩa tổng của hai vectơ, quy tắc ba điểm về tổng, quy tắc hình bình hành và các tính chất của tổng các vectơ.
*Lời giải:
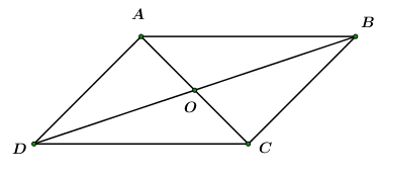
Ta có: (do ABCD là hình bình hành)
Do đó:
*Một số lý thuyết và dạng bài tập về tổng hai vectơ:
a) Lý thuyết: Tổng của hai vectơ
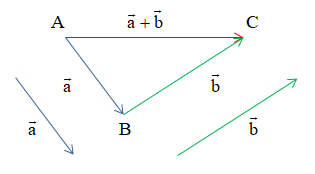
Cho hai vectơ và . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho . Khi đó được gọi là tổng của hai vectơ và và được kí hiệu là .
Vậy .
Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.
Quy tắc ba điểm
Với ba điểm M, N, P, ta có .
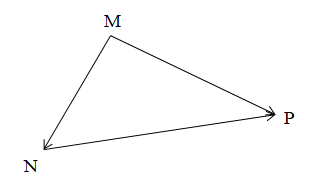Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.
Quy tắc hình bình hành
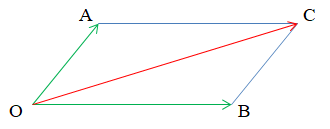
Nếu OACB là hình bình hành thì ta có .
b) Dạng bài tập
- Tính tổng hai vectơ
- Tính tích của vectơ với một số
- Phân tích vectơ
- Tọa độ vectơ, tọa độ một điểm
- Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vectơ
Xem thêm các bài viết liên quan hay, chi tiết
Trắc nghiệm Tổng hiệu của hai vecto có đáp án – Toán lớp 10
75 câu trắc nghiệm Vectơ nâng cao
Tổng và hiệu của hai vectơ và cách giải bài tập (2024) chi tiết nhất
Câu 9:
17/07/2024Cho 4 điểm A, B, C, D. Ta có:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có:
Vậy .
Câu 10:
21/07/2024Cho hình bình hành ABCD, M, N lần lượt là trung điểm của AD và BC. Khi đó,
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
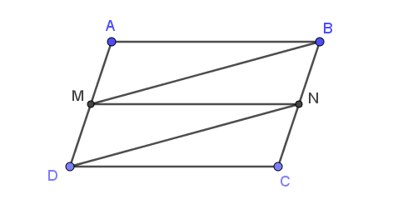
Do ABCD là hình bình hành nên AD // BC, AD = BC.
M, N lần lượt là trung điểm của AD và BC nên ta suy ra được:
AB = MN = DC, AM = MD = BN = NC, MN // AB // DC
Xét tam giác AMB và tam giác MDN có:
AM = MD
AB = MN
(hai góc đồng vị do MN // AB )
Do đó, tam giác AMB và tam giác MDN bằng nhau
⇒ MB = DN (1) và (2)
Từ (2) ta suy ra MB // DN (3)
Từ (1) và (3) ta suy ra:
Ta có: .