Dạng 5: Cách vẽ và xác định đồ thị hàm số bậc hai có đáp án
-
2271 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
16/07/2024
Xem đáp án
Hướng dẫn giải:
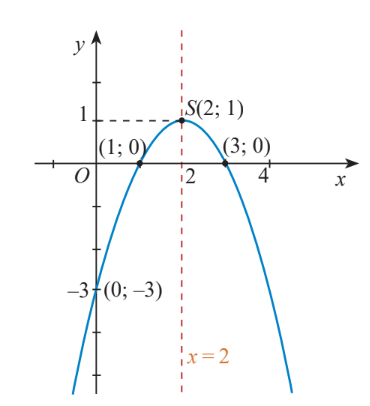
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 + 4x – 3 là một parabol (P):
– Có đỉnh S với hoành độ xS = 2, tung độ yS = 1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a = – 1 < 0;
– Cắt trục tung tại điểm có tung độ bằng –3, tức là đồ thị đi qua điểm có tọa độ (0; –3);
Ngoài ra, phương trình –x2 + 4x – 3 = 0 có hai nghiệm phân biệt x1 = 1 và x2 = 3 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (1; 0) và (3; 0).
Ta vẽ được đồ thị.
Câu 2:
18/07/2024 Xem đáp án
Hướng dẫn giải:
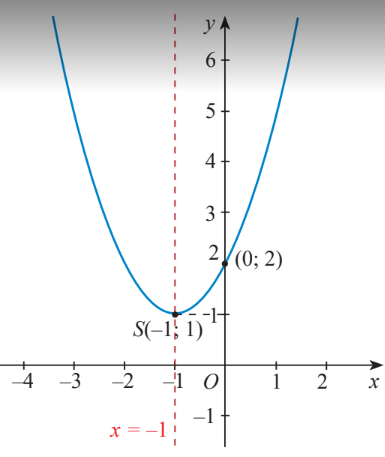
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x2 + 2x + 2 là một parabol (P):
– Có đỉnh S với hoành độ xS = –1, tung độ yS = 1;
– Có trục đối xứng là đường thẳng x = –1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 1 > 0;
– Cắt trục tung tại điểm có tung độ bằng 2, tức là đồ thị đi qua điểm có tọa độ (0; 2);
Ta vẽ được đồ thị
Câu 3:
12/07/2024Đồ thị của hàm số y = x2 – 4x + 3 là parabol có tọa độ đỉnh là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = x2 – 4x + 3 có a = 1, b = –4, c = 3. Đỉnh của parabol có:
Hoành độ: \(\frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2\)
Tung độ: \(\frac{{ - \Delta }}{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{{( - 4)}^2} - 4.1.3}}{{4.1}} = - 1\).
Do đó, parabol có tọa độ đỉnh là: (2; –1).
Câu 4:
12/07/2024Đồ thị của hàm số y = 2x2 + 8x + 1 là parabol có trục đối xứng là:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Xét hàm số y = 2x2 + 8x + 1 có a = 2, b = 8, c = 1 có trục đối xứng là đường thẳng :
\(x = \frac{{ - b}}{{2a}} = \frac{{ - 8}}{{2.2}} = - 2\).
Câu 5:
05/11/2024Đồ thị hàm số y = x2 – 4x + 3 là:
Xem đáp án
Đáp án đúng là: C.
Lời giải
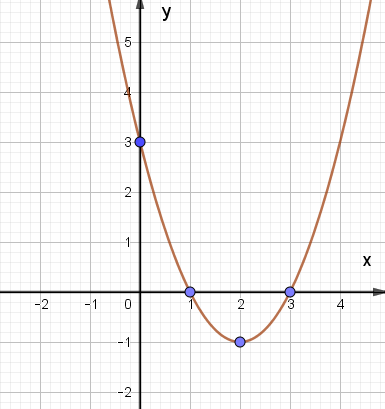
Xét hàm số y = f(x) = x2 – 4x + 3, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x2 – 4x + 3 là một parabol (P):
– Có đỉnh S với hoành độ xS = 2, tung độ yS = – 1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 1 > 0;
– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3);
– Ngoài ra, phương trình x2 – 4x + 3 = 0 có hai nghiệm phân biệt x1 = 1 và x2 = 3 nên đồ thị hàm số cắt trục hành tại hai điểm có tọa độ (1; 0) và (3; 0).
Ta vẽ được đồ thị như hình dưới:
*Phương pháp giải:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 3 đến 4 giá trị) tương ứng giữa x và y sao cho các điểm tương ứng nằm bên phải trục Oy.
Bước 3: Vẽ trục tọa độ Oxy và đánh dấu điểm O, các điểm đã lập trong bảng giá trị và các điểm đối xứng với chúng qua trục Oy.
Bước 4: Đồ thị hàm số y = a (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng. Vẽ đường cong parabol đi qua các điểm đã đánh dấu ta được đồ thị hàm số y = a (a ≠ 0) và kết luận.
*Lý thuyết:
- Đồ thị của hàm số: Đồ thị của hàm số y = a (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol)
+) Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+) Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Xem thêm
Các dạng bài tập Đồ thị hàm số y = a.x^2 (có đáp án 2024) và cách giải - Toán 9Câu 6:
22/07/2024Đồ thị hàm số y = 2x2 + 4x – 1 là hình:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
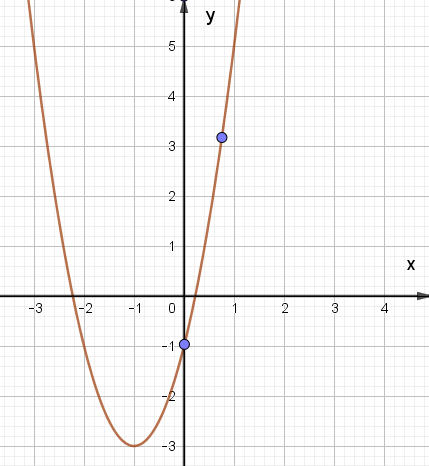
Xét hàm số y = 2x2 + 4x – 1, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x2 + 4x – 1 là một parabol (P):
– Có đỉnh S với hoành độ xS = –1, tung độ yS = –3;
– Có trục đối xứng là đường thẳng x = –1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 2 > 0;
– Cắt trục tung tại điểm có tung độ bằng –1, tức là đồ thị đi qua điểm có tọa độ (0; –1).
Ta vẽ được đồ thị như hình dưới:
Câu 7:
22/07/2024Đồ thị hàm số y = – x2 + 2x + 3 là hình:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
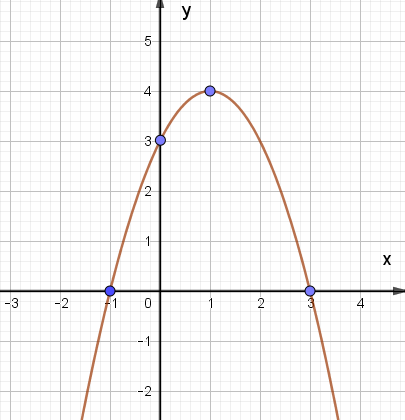
Xét hàm số y = –x2 + 2x + 3, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 + 2x + 3 là một parabol (P):
– Có đỉnh S với hoành độ xS = 1, tung độ yS = 4;
– Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a = – 1 < 0;
– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3);
– Ngoài ra, phương trình –x2 + 2x + 3 = 0 có hai nghiệm phân biệt là x1 = –1, x2 = 3. Do đó, đồ thị còn đi qua hai điểm (–1; 0), (3; 0).
Ta vẽ được đồ thị như hình dưới:
Câu 8:
11/07/2024Hình nào dưới đây là đồ thị của hàm số y = –3x2 + 6x ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
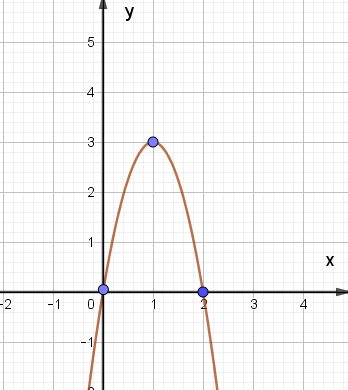
Xét hàm số y = –3x2 + 6x, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –3x2 + 6x là một parabol (P):
– Có đỉnh S với hoành độ xS = 1, tung độ yS = 3;
– Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a = – 3 < 0;
– Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua điểm có tọa độ (0; 0);
– Ngoài ra, phương trình –3x2 + 6x = 0 có hai nghiệm phân biệt là x1 = 0, x2 = 2. Do đó, đồ thị còn đi qua điểm (2; 0).
Ta vẽ được đồ thị như hình dưới:
Câu 9:
20/07/2024Hình nào dưới đây là đồ thị của hàm số y = 2x2 – 5 ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
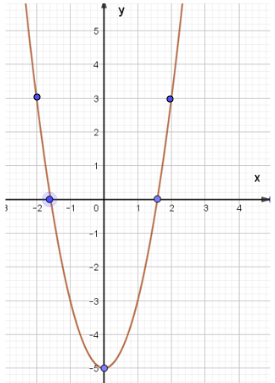
Xét hàm số y = 2x2 – 5, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x2 – 5 là một parabol (P):
– Có đỉnh S với hoành độ xS = 0, tung độ yS = –5;
– Có trục đối xứng là đường thẳng x = 0 (đường thẳng này chính là trục Oy);
– Bề lõm hướng lên trên vì a = 2 > 0;
– Ngoài ra, đồ thị hàm số y = 2x2 – 5 còn đi qua hai điểm (2; 3) và (–2; 3).
Ta vẽ được đồ thị như hình dưới:
Câu 10:
12/07/2024Đồ thị của hàm số y = –x2 – 4x + 5 nằm trong hình:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
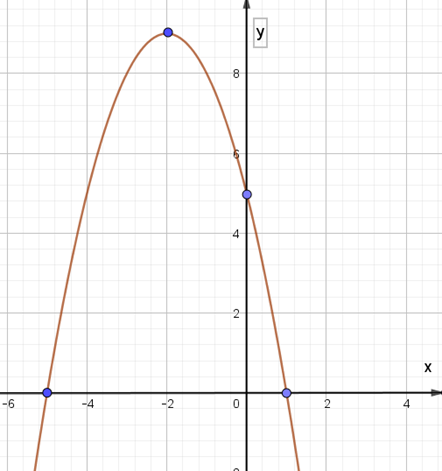
Xét hàm số y = –x2 – 4x + 5, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 – 4x + 5 là một parabol (P):
– Có đỉnh S với hoành độ xS = –2, tung độ yS = 9;
– Có trục đối xứng là đường thẳng x = –2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a = – 1 < 0;
– Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5);
– Ngoài ra, phương trình –x2 – 4x + 5 = 0 có hai nghiệm phân biệt là x1 = –5, x2 = 1. Do đó, đồ thị còn đi qua hai điểm (–5; 0), (1; 0).
Ta vẽ được đồ thị như hình dưới:
Câu 11:
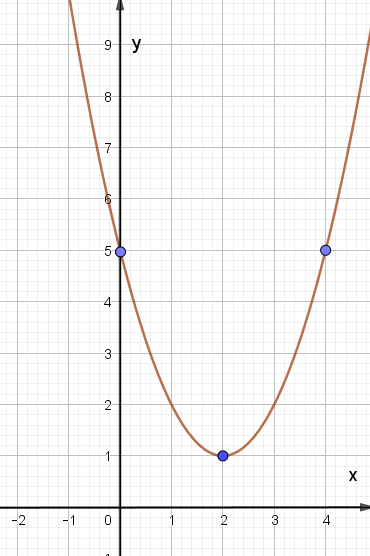
21/07/2024Vẽ đồ thị hàm số y = x2 – 4x + 5 ta được hình vẽ:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng: C.
Xét hàm số y = x2 – 4x + 5, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x2 – 4x + 5 là một parabol (P):
– Có đỉnh S với hoành độ xS = 2, tung độ yS = 1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 1 > 0;
– Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5);
– Điểm đối xứng với điểm (0; 5) qua trục đối xứng x = 2 là điểm (4; 5).
Ta vẽ được đồ thị như hình dưới:
Câu 12:
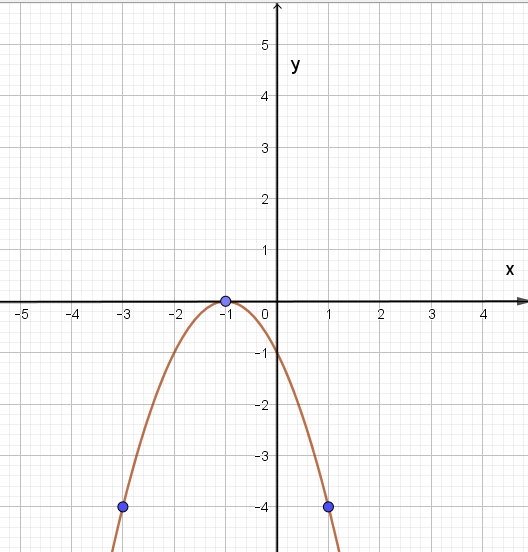
15/07/2024Vẽ đồ thị hàm số y = –x2 – 2x – 1 ta được hình vẽ:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = –x2 – 2x – 1, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x2 – 2x – 1 là một parabol (P):
– Có đỉnh S với hoành độ xS = –1, tung độ yS = 0;
– Có trục đối xứng là đường thẳng x = –1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay xuống dưới vì a = – 1 < 0;
– Cắt trục tung tại điểm có tung độ bằng –1, tức là đồ thị đi qua điểm có tọa độ (0; –1);
– Ngoài ra, đồ thị hàm số y = –x2 – 2x – 1 còn đi qua hai điểm (–3; –4) và (1; –4).
Ta vẽ được đồ thị như hình dưới:
