Câu hỏi:
05/11/2024 19,156Đồ thị hàm số y = x2 – 4x + 3 là:
A.
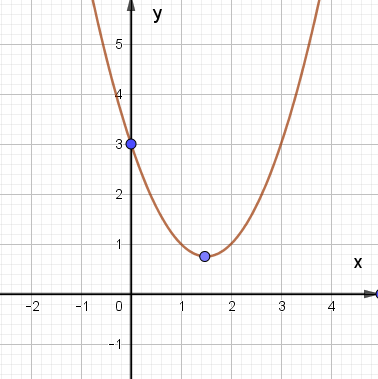

B.
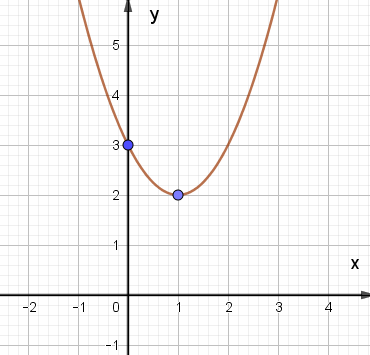

C.
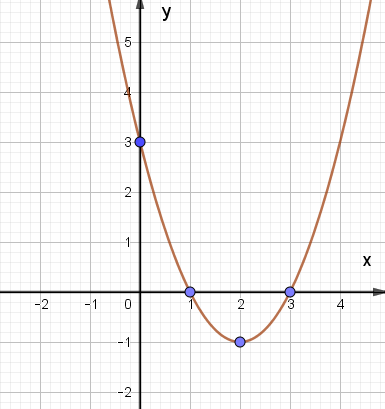

D.
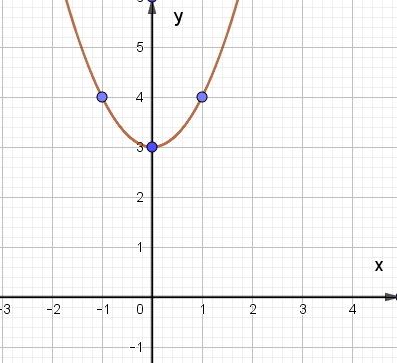

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C.
Lời giải
Xét hàm số y = f(x) = x2 – 4x + 3, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x2 – 4x + 3 là một parabol (P):
– Có đỉnh S với hoành độ xS = 2, tung độ yS = – 1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 1 > 0;
– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3);
– Ngoài ra, phương trình x2 – 4x + 3 = 0 có hai nghiệm phân biệt x1 = 1 và x2 = 3 nên đồ thị hàm số cắt trục hành tại hai điểm có tọa độ (1; 0) và (3; 0).
Ta vẽ được đồ thị như hình dưới:

*Phương pháp giải:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 3 đến 4 giá trị) tương ứng giữa x và y sao cho các điểm tương ứng nằm bên phải trục Oy.
Bước 3: Vẽ trục tọa độ Oxy và đánh dấu điểm O, các điểm đã lập trong bảng giá trị và các điểm đối xứng với chúng qua trục Oy.
Bước 4: Đồ thị hàm số y = ax2 (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng. Vẽ đường cong parabol đi qua các điểm đã đánh dấu ta được đồ thị hàm số y = ax2 (a ≠ 0) và kết luận.
*Lý thuyết:
- Đồ thị của hàm số: Đồ thị của hàm số y = ax2 (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol)
+) Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+) Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Xem thêm
Các dạng bài tập Đồ thị hàm số y = a.x^2 (có đáp án 2024) và cách giải - Toán 9
Đáp án đúng là: C.
Lời giải
Xét hàm số y = f(x) = x2 – 4x + 3, ta có:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x2 – 4x + 3 là một parabol (P):
– Có đỉnh S với hoành độ xS = 2, tung độ yS = – 1;
– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);
– Bề lõm quay lên trên vì a = 1 > 0;
– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3);
– Ngoài ra, phương trình x2 – 4x + 3 = 0 có hai nghiệm phân biệt x1 = 1 và x2 = 3 nên đồ thị hàm số cắt trục hành tại hai điểm có tọa độ (1; 0) và (3; 0).
Ta vẽ được đồ thị như hình dưới:

*Phương pháp giải:
Bước 1: Tìm tập xác định của hàm số.
Bước 2: Lập bảng giá trị (thường từ 3 đến 4 giá trị) tương ứng giữa x và y sao cho các điểm tương ứng nằm bên phải trục Oy.
Bước 3: Vẽ trục tọa độ Oxy và đánh dấu điểm O, các điểm đã lập trong bảng giá trị và các điểm đối xứng với chúng qua trục Oy.
Bước 4: Đồ thị hàm số y = ax2 (a ≠ 0) luôn đi qua gốc tọa độ O và nhận trục Oy làm trục đối xứng. Vẽ đường cong parabol đi qua các điểm đã đánh dấu ta được đồ thị hàm số y = ax2 (a ≠ 0) và kết luận.
*Lý thuyết:
- Đồ thị của hàm số: Đồ thị của hàm số y = ax2 (a ≠ 0) là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol)
+) Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.
+) Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.
Xem thêm
Các dạng bài tập Đồ thị hàm số y = a.x^2 (có đáp án 2024) và cách giải - Toán 9CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Đồ thị của hàm số y = x2 – 4x + 3 là parabol có tọa độ đỉnh là:
Câu 9:
Đồ thị của hàm số y = 2x2 + 8x + 1 là parabol có trục đối xứng là:


