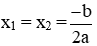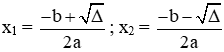Nội dung bài viết

    Xem thêm

    Tìm hai số u và v trong mỗi trường hợp sau

    Với giải câu hỏi 41 trang 58 sbt Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 7,817 17/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 9 Bài 2: Đồ thị của hàm số y=ax2a≠0

    Bài 41 trang 58 SBT Toán 9 Tập 2: Tìm hai số u và v trong mỗi trường hợp sau:

    a) u + v = 14, uv = 40

    b) u + v = –7, uv = 12

    c) u + v = –5, uv = –24

    d) u + v = 4, uv = 19

    e) u – v =10, uv = 24

    f) u2 + v2 = 85, uv =18

    Lời giải:

    a) Hai số u và v với u + v =14 và uv = 40 nên nó là nghiệm của phương trình x2 –14x + 40=0

    Δ’= (–7)2 – 1.40 = 49 – 40 = 9 > 0

    Phương trình có hai nghiệm phân biệt:

    x1=7+91=10;x1=7−91=4

    Vậy u = 10, v = 4 hoặc u = 4, v = 10

    b) Hai số u và v với u + v = –7 và uv = 12 nên nó là nghiệm của phương trình x2 + 7x + 12=0

    Δ = (7)2 – 4.1.12 = 49 – 48 = 1 > 0

    Phương trình có hai nghiệm phân biệt

    x1=−7+12.1=−62;x2=−7−12.1=−82=−4

    Vậy u = –3; v = –4 hoặc u = –4; v = –3

    c) Hai số u và v với u + v = –5 và uv = –24 nên nó là nghiệm của phương trình x2 + 5x – 24 =0

    Δ = (5)2 – 4.1.(–24) = 25 + 96 = 121 > 0

    Phương trình có hai nghiệm phân biệt

    x1=−5+112.1=62=3;x1=−5−112.1=−162=−8

    Vậy u = 3; v = –8 hoặc u = –8; v = 3.

    d) Hai số u và v với u +v = 4 và uv = 19 nên nó là nghiệm của phương trình x2 – 4x + 19 = 0

    Δ’ = (–2)2 – 1.19 = 4 – 19 = –15 < 0

    Phương trình vô nghiệm nên không có giá trị nào của u và v thỏa mãn điều kiện bài toán

    e) Ta có: u – v = 10 ⇒ u + (–v) = 10

    u.(–v) = –uv = –24

    Do đó, u, –v là nghiệm của phương trình: x2 – 10x – 24 = 0

    Δ’ = (–5)2 – 1.(–24) = 25 +24 = 49 > 0

    Phương trình có hai nghiệm phân biệt

    x1=5+491=121=12;x2=5−491=−2

    Vậy u = 12 , –v = –2 hoặc u = –2, –v = 12 suy ra u = 12, v = 2 hoặc u = –2 , v = –12

    f) Hai số u và v với u2 + v2 = 85 và uv = 18 suy ra: u2v2 = 324 nên u2 và v2 là nghiệm của phương trình x2 – 85x + 324 = 0

    Δ = (–85)2 – 4.1.324 = 7225 – 1296 = 5929 > 0

    Phương trình có hai nghiệm phân biệt:

    x1=85+772.1=1622=81;x2=85−772.1=82=4

    Ta có: u2 = 81 ,v2 = 4 suy ra: u = ±9, v = ± 2

    hoặc u2 = 4, v2 = 81 suy ra: u = ± 2, v = ± 9

    Vậy nếu u = 9 thì v = 2 hoặc u =–9, v =–2

    nếu u = 2 thì v = 9 hoặc u = –2 ,v = –9.

    *Phương pháp giải:

    Dựa vào: Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình:x^2 -Sx+P=0

    Dựa vào điều kiện:S^2-4P > hoặc =0

    *Lý thuyết:

    Phương trình bậc hai một ẩn có dạng ax2 + bx + c = 0 (a ≠ 0). Để giải phương trình ta làm như sau

    B1: Xác định các hệ số a, b, c

    B2: Tính ∆ = b2 - 4ac

    + Nếu ∆ < 0 thì phương trình vô nghiệm

    + Nếu ∆ = 0 thì phương trình có nghiệm kép: Phương pháp giải phương trình bậc hai một ẩn hay, chi tiết

    + Nếu ∆ > 0 thì phương trình có 2 nghiệm phân biệt:

    Phương pháp giải phương trình bậc hai một ẩn hay, chi tiết

    Xem thêm

    Lý thuyết Phương trình bậc hai một ẩn - Toán 9 Kết nối tri thức

    TOP 40 câu Trắc nghiệm Phương trình bậc nhất hai ẩn (có đáp án 2024) – Toán 9

    Xem thêm lời giải sách bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 35 trang 57 SBT Toán 9 Tập 2: Giải phương trình rồi kiểm nghiệm...

    Câu hỏi 36 trang 57 SBT Toán 9 Tập 2: Không giải phương trình, dùng hệ thức...

    Câu hỏi 37 trang 57 SBT Toán 9 Tập 2: Tính nhẩm nghiệm của các phương...

    Câu hỏi 38 trang 57 SBT Toán 9 Tập 2: Dùng hệ thức Vi–ét để tính nhẩm...

    Câu hỏi 39 trang 57 SBT Toán 9 Tập 2: Chứng tỏ rằng phương trình...

    Câu hỏi 40 trang 57 SBT Toán 9 Tập 2: Dùng hệ thức Vi–ét để tìm nghiệm...

    Câu hỏi 42 trang 58 SBT Toán 9 Tập 2: Lập phương trình có hai nghiệm là hai số...

    Câu hỏi 43 trang 58 SBT Toán 9 Tập 2: Cho phương trình...

    Câu hỏi 44 trang 58 SBT Toán 9 Tập 2: Cho phương trình...

    Bài tập bổ sung

    Câu hỏi 1 trang 58 SBT Toán 9 Tập 2: Giả sử x1, x2 là hai nghiệm...

    Câu hỏi 2 trang 58 SBT Toán 9 Tập 2: Giả sử x1, x2 là hai nghiệm...

    Câu hỏi 3 trang 58 SBT Toán 9 Tập 2: Dùng định lý Vi – ét, hãy chứng tỏ rằng...

    Câu hỏi 4 trang 59 SBT Toán 9 Tập 2: Cho phương trình...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 7,817 17/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: